卡特兰数Catalan——定义、公式、模型总结

推荐：卡特兰数总结

定义：

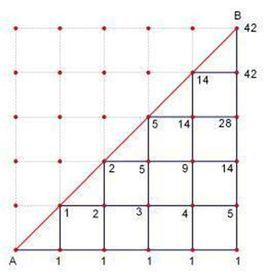
f(i)表示，从(0,0)出发，到（i，i），每次只能向上或者向右走，并且不越过红线的方案数。

这个图片的点上的数字，其实告诉我们f[i]，就可以根据这个n方dp得到。

其实是由这个阶梯推过来的。

也是之后的经典模型

公式：

来自百度百科

定义式：

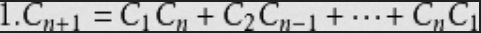
为什么是对的？考虑第一次走到(y=x)的情况大概图长这样：中间空出一行为了强制必须向上走

这个式子是n^2的，太low了。

h(n)=c(2n,n)-c(2n,n-1)(n=0,1,2,...)

这个式子推法：

从A到目标点C(n,n)的方案数有：

C(2*n,n)，即从2*n步中，选择n步向上走的方案数。

那么，我们不能超过绿线y=x，就意味着不能触碰红线y=x+1

发现，刚才每一个非法的方案数中，如果把碰到红线和碰到红线之前的路径，关于红线对称一下，碰到红线之后的路径不用管，

一定是一个从B点，即(-1,1)出发到C的方案。

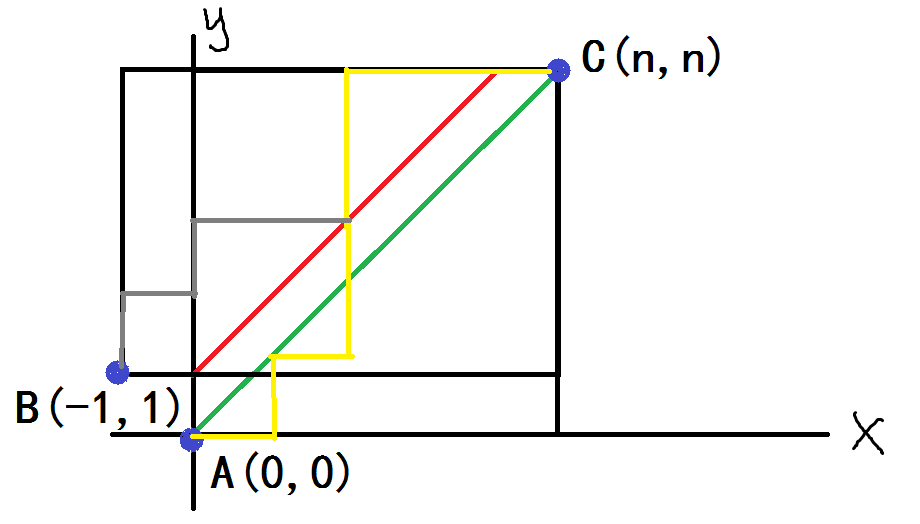
黄线是一个不合法的方案，黄线在红线之前的部分，对称成灰色的路径，再和红色之后的黄色路径拼在一起，就是一个从B开始到C的路径。

发现，这个还是 一 一对应的！！

从B到C的方案是：C(2*n,n-1)

所以，从A到C的合法方案，就是f[n]=C(2*n,n)-C(2*n,n-1)

h(n)=C(2n,n)/(n+1) (n=0,1,2,...)

这个把上面的公式组合数展开化简即可。

模型与例题

答案通常与卡特兰数第k项直接相关。

1.火车进栈

这是一个卡特兰数经典入门题目。

直接输出h[n]

我们假设最后出栈的是k

那么k之前的所有数都进栈出栈了。k之后所有数也都进栈出栈了

k两边就是两个互相独立的子问题。

方案是：a[n-k]*a[k-1],又因为k可以取到1~n的任何数。

所以根据加法原理，a[n]=a[n-1]*a[1]+a[n-2]*a[2]+...a[1]*a[n-1]

就是卡特兰数的递推式子了。

也可以这样想，一节车厢进栈，代表向右走，出栈，代表向左走，

因为不存在一个时刻，出栈的总次数大于进栈的总次数。

恰好和从(0,0）到(n,n)不越过y=x方案数一致。

这个模型也证明了卡特兰数的两个公式其实是统一的。

2.合法括号序列 牛客网NOIP赛前集训营-普及组（第二场）

长度为2k的合法括号序列有 h[k]个。

证明：把左括号抽象为向右走，右括号抽象为向上走，

然后同上可以证明了。

其实是火车进栈的抽象版本。

牛客9.16普及组T4

3.0/1走

即每次向右走，或者向上走，不越过y=x的方案数。

这就是卡特兰数基本定义模型了。

对于类似必须越过y=x至少一次，就是不合法的C(2n,n-1)了

对于恰好越过一次，其实也是C(2n,n)，相当于第一次碰到绿线之后的路径关于绿线对称过去，还是一样的。

但是可能边界考虑减一减。

 

4.凸包三角形划分。

留坑。

5.n个点二叉树不同形态方案数。

假设根左子树大小为k-1个，右子树大小为n-k个

那么，这种情况下的方案数就是a[k-1]*a[n-k]

因为k可以取1~n，所以，

就是之前的a[n]=a[n-1]*a[1]+a[n-2]*a[2]+...a[1]*a[n-1]了。

6.阶梯

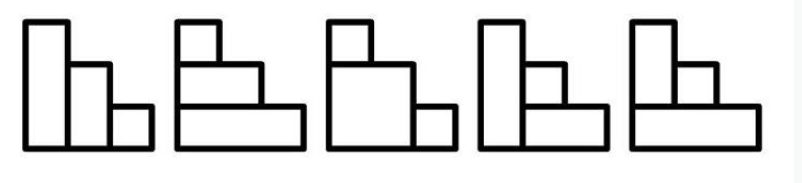
用n个矩形完全不重叠覆盖n阶阶梯方案数。

发现，左下角一定会被一个矩形覆盖（废话）

这个矩形假设左上有k-1个矩形，右下有n-k个矩形，（或者说分成了两个子问题的小阶梯形）

那么，这种情况下的方案数就是a[k-1]*a[n-k]

因为k可以取1~n，所以，

就是之前的a[n]=a[n-1]*a[1]+a[n-2]*a[2]+...a[1]*a[n-1]了。

[AHOI2012]树屋阶梯

总结：

①会推：那就推。

一般从两个方面的模型考虑：

1.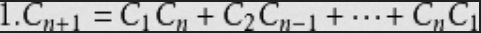是否可以得出这个式子。、

2.是否能够转化成这个图的模型问题。

②不会？那就打表找规律咯。。。。

记住前几项：1,1,2,5,14,42（第0项开头）

然后可以再尝试证明、

另类：施罗德数