视差滚动（Parallax Scrolling）的一点小心得

下面内容来源于我知乎的这个答案：http://www.zhihu.com/question/20990029/answer/21436067

假期有空，整理到博客园这边，并做了一些语境的调整。

———————— 正文 ————————

先说说什么是视差。

视差滚动（Parallax Scrolling）是指多层背景以不同的速度移动，形成立体的运动效果，带来非常出色的视觉体验。

一般把网页解剖为：背景层、内容层 和 悬浮层(贴图层)。

当滚动鼠标滚轮的时候，各图层以不同速度移动，形成视差的效果。这就是时差滚动的大致原理。

原理是这样，但落实到技术细节上时，实现的方法却各种各样。

我个人大致归纳了一下：

1、以 “页面滚动条” 作为 “视差动画进度条” 的；

2、以 “滚轮刻度” 当作 “动画帧度” 去播放动画的（或者直接称为“隐藏进度条”）；

3、鉴听mousewheel事件，事件被触发即播放动画，实现“翻页”效果；

下面就简单说说1类。

为什么是1类呢？因为它很直观，和我们日常接触到的视频播放器是一样的：

（页面滚动条 等同于 播放器进度条）

下面，以Every Last Drop这个页面做为分析对象。

做滚动网页的时候，是怎么实现页面的翻页？

首先，根据页面动画所需的分镜，去等比划分进度条。

例如：共有11个分镜，则分镜大致可以划分为：0%、10%、20%、30% .... 100%

但需要注意的是，整个滚动过程实际分为两个部分：分镜切换 和 分镜动画。

我们要预先划分好他们的比例，如：每一个分镜，2%的进度用于分镜切换，7%的进度用于分镜动画。

则进度大致可以划分为：

------------------------------------------

0%(初始，分镜1)

↓

(消耗2%用于切换分镜)

↓

2%(完全进入分镜2）

↓

(消耗8%用于分镜动画的播放)

↓

10%(分镜2动画播放完毕)

↓

(消耗2%用于切换分镜)

↓

12%(完全进入分镜3）

↓

...（略）

------------------------------------------

按照上面的划分，当进度条滚动到10%的时候，就要开始进行分镜2到分镜3的切换，也就是所谓的翻页。当滚动到12%时，翻页结束。其他分镜如此类推。

这边推荐一个做视差滚动的插件：Jarallax(Welcome to Jarallax.com)

设计思路清晰，API设计也很直观。依赖于jQuery1.7的版本，再高的版本就不支持了哦！

另外，作者貌似已经没有维护了...

做视差滚动，大家做关注的莫过于：如何让滚动更加平滑？

但这个问题就太大了，这边我就简单回答一下吧（不细谈前端技术层面的优化，如：DOM数量、页面渲染优化这些）。

开头处，我提到的三种实现分类，实际上是这样一个情况：

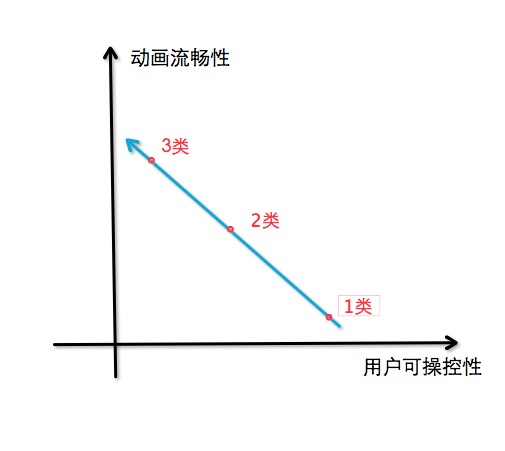
1类是最自由的，用户甚至可以直接调整进度条，实现“快进”。

在这种设计下，用户鼠标滚轮的最小刻度，就是动画的一帧。因为不同浏览器之间，鼠标滚轮的最小刻度是不一样的。这就导致了，在不同浏览器之间，页面滚动过程中，动画播放的帧率是有差异的。如果遇到奇葩浏览器，鼠标滚动的最小刻度很大，动画甚至会出现“掉帧”的情况。

解决方法很简单，一般采取增加页面长度的方式，来稀释鼠标滚轮的最小刻度。

但还是会有一些情况出现，如户快拖动进度条时，“掉帧”的情况难免还是会出现。

3类的实现，滚轮只是动画的触发按钮。当用户滚动了一下鼠标，之前设计好的动画就开始播放。当播放结束后，对滚动事件的监听，才会重新被激活。这种设计，弱化了交互，但提供了更优质的动画展现。因为动画的播放时间和帧率不是用户控制的，是事先代码所设定好的。

2类就不说了，介乎与1和3之间。

简单的说，鱼(流畅)与熊掌(操控性)不可得兼。

关于1类，就先到这里吧。以后有机会，再跟大家聊聊其他两个类别的。

本文地址：http://www.cnblogs.com/maplejan/p/3538157.html