巴塞尔问题(Basel problem)的多种解法——怎么计算$\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\cdots$ ?

（PS：本文会不断更新）

$\newcommand\R{\operatorname{Res}}$

如何计算$\zeta(2)=\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\cdots$? 这个问题是在1644年由意大利数学家蒙哥利（Pietro Mengoli）提出的，而大数学家欧拉于1735年第一次解决了这个问题。他得出著名的结果：
\[\sum_{k=1}^{\infty}\frac{1}{k^2}=\frac{\pi^2}{6}\]

解决这个问题的方法在近代不断涌现。这里我从各处摘抄到一些方法，列举在此，仅供大家参考。

如有错误，请向我指出，谢谢！（PS：最近发现忻州师范学院某网页抄了我博客后不给Reference，希望大家明辨是非）

首先，我们需要知道这个问题的等价形式,将这个数列除以4，我们自然得到$\sum_{k=1}^{\infty} \frac{1}{(2k)^2}=\frac{\pi^2}{24}$,从而我们只需证明
\[\sum_{k=1}^{\infty}\frac{1}{(2k-1)^2}=\frac{\pi^2}{8}\]
而以下某些证明会用到这一点。

目录

• 1 欧拉的证明
• 2 一个初等的证明
• 3 数学分析的证明
• 4 又一个数学分析的证明
• 5 复分析的证明
• 6 复数积分的证明
• 7 泰勒公式的证明
• 8 复分析的证明
• 9 傅里叶分析的证明
• 10 傅里叶分析的证明
• 11 傅里叶分析的证明
• 12 泊松公式的证明
• 13 概率论的证明
• 14 积分+函数方程的证明
• 15 初等三角恒等式的证明
• 16 三角多项式的证明
• 17 积分的证明
• 18 Fejér核证明
• 19 利用Gregory定理的证明
• 20 数论的证明（比较精彩）
• 21 初等三角恒等式的证明
• 22 伯努利数的证明
• 23 超几何正切分布的证明

证明1：欧拉的证明

欧拉的证明是十分聪明的。他只是将幂级数同有限的多项式联系到了一起，就得到了答案。首先注意到
\[\sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots\]
从而
\[\frac{\sin(x)}{x} = 1 - \frac{x^2}{3!} + \frac{x^4}{5!} - \frac{x^6}{7!} + \cdots\]
但是$\frac{\sin{x}}{x}$的根集，为
\[x=n\cdot \pi,\mbox{ }(n = \pm1, \pm2, \pm3, \dots).\]
故我们可以假定
\begin{align}
\frac{\sin(x)}{x} & {} =
\left(1 - \frac{x}{\pi}\right)\left(1 + \frac{x}{\pi}\right)\left(1 - \frac{x}{2\pi}\right)\left(1 + \frac{x}{2\pi}\right)\left(1 - \frac{x}{3\pi}\right)\left(1 + \frac{x}{3\pi}\right) \cdots \notag\\
& {} = \left(1 - \frac{x^2}{\pi^2}\right)\left(1 - \frac{x^2}{4\pi^2}\right)\left(1 - \frac{x^2}{9\pi^2}\right) \notag\cdots.
\end{align}
（PS：欧拉似乎没有证明这个无穷积，直到100年后魏尔斯特拉斯得到了他著名的“魏尔斯特拉斯分解定理”（Weierstrass factorization theorem，详情可见wiki相应条目）。利用这个方法得到函数时要特别小心，我以前看到的一个反例就可以说明这个问题)

从而我们对这个无穷乘积的$x^2$项进行研究，可以知道
\[-\left(\frac{1}{\pi^2} + \frac{1}{4\pi^2} + \frac{1}{9\pi^2} + \cdots \right) =
-\frac{1}{\pi^2}\sum_{n=1}^{\infty}\frac{1}{n^2}.\]
所以
\[-\frac{1}{6} =
-\frac{1}{\pi^2}\sum_{n=1}^{\infty}\frac{1}{n^2}.\]
这样就得到了答案。

注：欧拉给出过严谨的证明，但是由于他的第一个证明太广为人知，所以有时候会认为他没给出真正的证明。不过贴吧里的 tq唐乾 吧友提醒了我，实际上，欧拉有他真正的证明。是通过如下方式：首先令$N$为奇数

$$z^n-a^n=(z-1)\prod_{k=1}^{(n-1)/2}(z^2-2az\cos{\frac{2k\pi}{n}}+a^2)$$
令$z=1+x/N,a=1-x/N$,且n=N,有
\begin{align*}\left(1+\frac{x}N\right)^N-\left(1+\frac{x}N\right)^N &=\frac{2x}{N}\prod_{k=1}^{(N-1)/2}\left(2+\frac{2x^2}{N^2}-2\left(1-\frac{x^2}{N^2}\right)\cos{\frac{2k\pi}{N}}\right)\\
&=\frac{2x}{N}\prod_{k=1}^{(N-1)/2}\left(\left(1-\cos{\frac{2k\pi}{N}}\right)+\frac{x^2}{N^2}\left(1+\cos{\frac{2k\pi}{N}}\right)\right)\\
&=C_N x \prod_{k=1}^{(N-1)/2}\left(1+\frac{x^2}{N^2}\frac{1+\cos{(2k\pi/N)}}{1-\cos{(2k\pi/N)}}\right)
\end{align*}

考虑一次项系数知道$C_N=2$成立，而在$N\to\infty$时，左边是$e^x-e^{-x}$,右边通过$\cos{y}\approx 1-y^2/2$,那么右边就是$1+x^2/(k^2\pi^2)$的乘积，也就是

$$\frac{e^x-e^{-x}}{2}=x\prod_{k=1}^{\infty}\left(1+\frac{x^2}{k^2\pi^2}\right)$$

比较三次项系数可知答案

证明2：一个初等的证明
以下证明第一次来自Ioannis Papadimitriou于1973年在American Math Monthly 80(4):424-425页发表的。Apostol在同一份杂志425-430发表了用这个方法计算$\zeta(2n)$的方法。

这似乎是这个问题最“初等”的一个证明了，只需要知道三角函数相应知识就能够完成。我们先证明一个恒等式：

Lemma: 令$\omega_m = \frac{\pi}{2m+1}$,则
\[\cot^2{\omega_m}+\cot^2{(2\omega_m)}+\cdots\cot^2{(m\omega_m)}=\frac{m(2m-1)}{3}.\]

证明：由于
\begin{align*}
\sin{n\theta}&=\binom{n}{1}\sin{\theta}\cos^{n-1}{\theta}-\binom{n}{3}\sin^3{\theta}\cos^{n-3}{\theta}+\cdots \pm \sin^n{\theta}\\
&=\sin^n{\theta}\left(\binom{n}{1}\cot^{n-1}{\theta}-\binom{n}{3}\cot^{n-3}{\theta}+\cdots \pm 1\right)
\end{align*}
很显然，令$n=2m+1$,则我们有$\cot^2{\omega_m},\cot^2{(2\omega_m)}\cdots \cot^2{(m\omega_m)}$为多项式
\[\binom{n}{1}x^{m}-\binom{n}{3}x^{m-1}+\cdots \pm 1\]
的根。从而利用韦达定理我们就完成了引理的证明。$\square$

由于三角不等式 $\sin{x}<x<\tan{x}$ 在$x\in(0,\pi/2)$成立，我们知道了$\cot^2{x}<\frac{1}{x^2}<1+\cot^2{x}$.对于$\omega_m,2\omega_m\cdots$带入得到
\[\sum_{k=1}^{m}\cot^2{(k\omega_m)}<\sum_{k=1}^{m}\frac{1}{k^2\omega_m^2}<m+\sum_{k=1}^{m}\cot^2{(k\omega_m)}\]
所以应用上面引理，就可以得到
\[\frac{m(2m-1)\pi^2}{3(2m+1)^2}<\sum_{k=1}^{m}\frac{1}{k^2}<\frac{m(2m-1)\pi^2}{3(2m+1)^2}+\frac{m\pi^2}{(2m+1)^2}\]
令m趋于无穷大，结论自然就成立了。

证明3：数学分析的证明
这个证明来自Apostol在1983年的“Mathematical Intelligencer”,只需要简单的高数知识。

注意到恒等式
\[\frac{1}{n^2}=\int_{0}^1\int_0^1 x^{n-1}y^{n-1}dxdy\]
利用单调收敛定理(Monotone Convergence Theorem)，立即得到
\[\sum_{n=1}^{\infty}\frac{1}{n^2}=\int_{0}^1\int_0^1\left(\sum_{n=1}^{\infty}(xy)^{n-1}\right)dxdy=\int_{0}^1\int_0^1 \frac{1}{1-xy}dxdy\]
通过换元$(u,v)=((x+y)/2,(y-x)/2)$,也就是$(x,y)=(u-v,u+v)$故
\[\sum_{n=1}^{\infty}\frac{1}{n^2}=2\iint_S\frac{1}{1-u^2+v^2}dudv\]
$S$是由点$(0,0),(1/2,-1/2),(1,0),(1/2,1/2)$构成的正方形，利用正方形的对称性，那么
\begin{align*}
2\iint_S\frac{1}{1-u^2+v^2}dudv&=4\int_{0}^{1/2}\int_{0}^{u}\frac{1}{1-u^2+v^2}dvdu+4\int_{1/2}^{1}\int_{0}^{1-u}\frac{1}{1-u^2+v^2}dvdu\\
&=4\int_{0}^{1/2}\frac{1}{\sqrt{1-u^2}}\arctan{\left(\frac{u}{\sqrt{1-u^2}}\right)}du\\&\quad+4\int_{1/2}^{1}\frac{1}{\sqrt{1-u^2}}\arctan{\left(\frac{1-u}{\sqrt{1-u^2}}\right)}du
\end{align*}
利用恒等式$\arctan{(u/\sqrt{1-u^2})}=\arcsin{u},\arctan{((1-u)/\sqrt{1-u^2})}=\frac{\pi}{4}-\frac{1}{2}\arcsin{u}$,就能够得到
\begin{align*}\sum_{n=1}^{\infty}\frac{1}{n^2}&=4\int_0^{1/2}\frac{\arcsin{u}}{\sqrt{1-u^2}}du+4\int_{1/2}^{1}\frac{1}{\sqrt{1-u^2}}\left(\frac{\pi}{4}-\frac{\arcsin{u}}{2}\right)du\\
&=[2\arcsin{u}^2]_0^{1/2}+[\pi\arcsin{u}-\arcsin{u}^2]_{1/2}^{1}\\
&=\frac{\pi^2}{18}+\frac{\pi^2}{2}-\frac{\pi^2}{4}-\frac{\pi^2}{6}+\frac{\pi^2}{36}\\
&=\frac{\pi^2}{6}
\end{align*}

证明4:数学分析的证明

(Calabi, Beukers & Kock.)同样利用上一问的结论,不过这次我们计算的是：

\[\sum_{n=0}^{\infty}\frac{1}{(2n+1)^2}=\int_0^1\int_0^1\frac{dxdy}{1-x^2y^2}\]

做代换$$(u,v)=\left(\arctan{x}\sqrt{\frac{1-y^2}{1-x^2}},\arctan{x}\sqrt{\frac{1-x^2}{1-y^2}}\right)$$

从而有$(x,y)=\left(\frac{\sin{u}}{\cos{v}},\frac{\sin{v}}{\cos{u}}\right)$

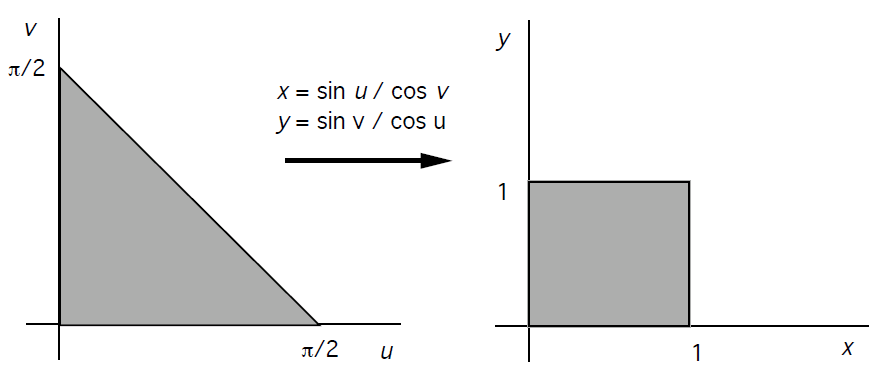
雅可比行列式即为

\begin{align*}
\frac{\partial (x,y)}{\partial(u,v)}&=\begin{vmatrix}
\cos{u}/\cos{v} & \sin{u}\sin{v}/\cos{v}^2 \\
\sin{u}\sin{v}/\cos{u}^2 & \cos{v}/\cos{u} 
\end{vmatrix}\\
&=1-\frac{\sin^2u\sin^2v}{\cos^2u\cos^2v}=1-x^2y^2
\end{align*}

从而$$\frac{3}{4}\zeta(2)=\sum_{n=0}^{\infty}\frac{1}{(2n+1)^2}=\iint_{A}dudv$$

其中$A=\{(u,v)|u>0,v>0,u+v<\frac{\pi}{2}\}$,从而$\zeta(2)=\frac{\pi^2}{6}$成立!$\square$

证明5:复分析的证明

这个证明在很多复分析书上都有。我们同样可以利用留数计算该结果,考虑$f(x)=z^{-2} \cot{\pi z}$,积分路径$P_n$为在中心为原点的长形如图

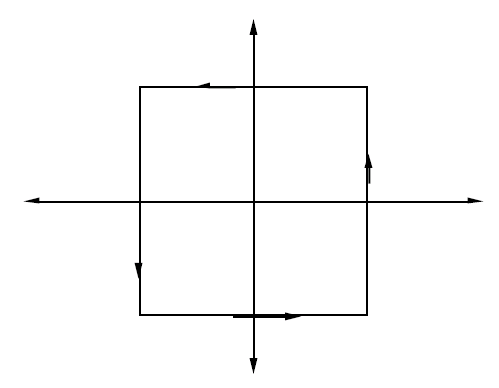
实轴交点为$\pm(n+1/2)$,复轴为$\pm ni$,而若$\pi z=x+iy$,直接计算可得

$$|\cot{\pi z}|^2=\frac{\cos^2{x}+\sinh^2{y}}{\sin^2{x}+\sinh^2{y}}$$，从而很容易就能知道$|\cot{\pi z}|<2$对于每根积分曲线成立，于此同时，$|z|\ge n$成立,从而有

\[\left|\oint_{P_n}z^{-2}\cot{\pi z}\right|\le\frac{2}{n^2}(8n+2)\]

成立，在$n\to\infty$时，该积分值趋于$0$.

利用留数定理，则有

$$2\pi i\sum_{k=-\infty}^{\infty}\R(z^{-2}\cot{\pi z},k)=\lim_{n\to\infty}\oint_{P_n}z^{-2}\cot{\pi z}dz=0$$

而每一点的留数，计算有$\R(z^{-2}\cot{\pi z},0)=-\pi/3$,$\R(z^{-2}\cot{\pi z},k)=1/(\pi k^2)(k\not=0,k\in\mathbb{Z})$,从而有

$$\sum_{k=1}^{\infty}\frac{2}{\pi k^2}=\frac{\pi}{3}$$

答案显而易见了。

证明6:复数积分的证明

本证明由Dennis C.Russell给出。考虑积分$$I=\int_0^{\pi/2}\ln(2\cos{x})dx$$

那么利用$\cos$的欧拉公式

$2\cos{x}=e^{ix}+e^{-ix}=e^{ix}(1+e^{-2ix})$从而$\ln(2\cos{x})=\ln(e^{ix})+\ln(1+e^{-2ix})=ix+\ln(1+e^{-2ix})$在积分中代换得
\begin{align*}
I&=\int_0^{\pi/2}ix+\ln(1+e^{-2ix})dx\\&=i\frac{\pi^2}{8}+\int_0^{\pi/2}ln(1+e^{-2ix})dx
\end{align*}
再利用$\ln{(1+x)}$的泰勒展开,也就是
$$\ln(1+x)=x-x^2/2+x^3/3-x^4/4+\cdots$$
代入知为
\[\ln(1+e^{-2ix})=e^{2ix}-e^{-4ix}/2+e^{-6ix}/3+\cdots\]
从而积分就有
\[\int_0^{\pi/2}\ln{(1+e^{-2ix})}dx=-\frac{1}{2i}(e^{-i\pi}-1-\frac{e^{-2i\pi}-1}{2^2}+\frac{e^{-3i\pi}-1}{3^2}-\frac{e^{-4i\pi}-1}{4^2}+\cdots)\]
但是由于$e^{-i\pi}=-1$,原式变为
\[\int_0^{\pi/2}\ln(1+e^{-2ix})dx=\frac{1}{i}\sum_{k=1}^{\infty}\frac{1}{(2k-1)^2}=\frac{-3i}{4}\zeta(2)\]
故如前面式子有
\[I=i\left(\frac{\pi^2}{8}+\frac{-3}{4}\zeta(2)\right)\]
由于左边是实数，右边是纯虚数，从而只能两边都为0，即$\zeta(2)=\frac{\pi^2}{6}$,这还给了我们一个副产品，就是\[\int_0^{\pi/2}\ln(\cos{x})dx=-\frac{\pi}{2}\ln{2}\]

证明7:泰勒公式证明

(Boo Rim Choe 在1987 American Mathematical Monthly上发表)利用反三角函数$\arcsin{x}$的泰勒展开

$$\arcsin{x}=\sum_{n=0}^{\infty}\frac{1\cdot 3\cdots (2n-1)}{2\cdot 4\cdots (2n)}\frac{x^{2n+1}}{2n+1}$$对于$|x|\le 1$成立，从而令$x=\sin{t}$,有
$$t=\sum_{n=0}^{\infty}\frac{1\cdot 3\cdots (2n-1)}{2\cdot 4\cdots (2n)}\frac{\sin^{2n+1}t}{2n+1}$$
对于$|t|\le\frac{\pi}{2}$成立，但由于积分
$$\int_0^{\pi/2}\sin^{2n+1}{x}dx=\frac{2\cdot 4\cdots (2n)}{3\cdot 5\cdots (2n+1)}$$
故而对两边从$0$到$\pi/2$积分有
\[\frac{\pi^2}{8}=\int_0^{\pi/2}tdt=\sum_{n=0}^{\infty}\frac{1}{(2n+1)^2}\]
同样可得

证明8:复分析证明

(T. Marshall 在American Math Monthly,2010)对于$z\in D=\mathbb{C}\backslash\{0,1\}$, 令

$$R(z)=\sum\frac{1}{\log^2 z}$$

这个和是对于每一个$\log$的分支加起来. 在 $D$ 中所有点有领域使$\log(z)$的分支解析.由于这个级数在 $z=1$之外一致收敛, $R(z)$在 $D$上解析.

这里有几个Claim:

1. 当$z\to0$时，级数每一项趋于$0$.由于一致收敛我们知道$z=0$是可去奇点，我们可令$R(0)=0$.
2. $R$ 的唯一奇点是 $z=1$的二阶极点，是由 $\log z$的主分支.我们有$\lim_{z\to1}(z-1)^2R(z)=1$.
3. $R(1/z)=R(z)$.

由于 1.和 3.有 $R$ 在$\mathbb{C}\cup \{\infty\}$（扩充复平面）上亚纯,从而是有理函数. 从2知道$R(z)$的分母是$(z-1)^2$. 由于$R(0)=R(\infty)=0$, 分子就是$az$. 而2. 说明$a=1$, 也就是
$$R(z)=\frac{z}{(z-1)^2}.$$

现在令$z=e^{2\pi i w}$ 得到
$$\sum\limits_{n=-\infty}^{\infty}\frac{1}{(w-n)^2}=\frac{\pi^2}{\sin^2(\pi w)}$$
也就是说$$\sum\limits_{k=0}^{\infty}\frac{1}{(2k+1)^2}=\frac{\pi^2}{8},$$
可立刻的到$\zeta(2)=\pi^2/6$ .

证明9:傅立叶分析证明

考虑函数$f(x)=x^2,x\in(-\pi,\pi)$,将其傅立叶展开

\[f(x)=\dfrac{\pi ^{2}}{3}+\sum_{n=1}^{\infty }\left( (-1)^{n}\dfrac{4}{n^{2}}
\cos nx\right)\]

显而易见，代入$f(0)$即可得到答案

证明10:傅立叶分析证明

考虑函数$f(x)=x,x\in(-\pi,\pi)$,将其傅立叶展开

\[f(x)=2\sum_{n=1}^{\infty }\left( \dfrac{(-1)^{n+1}}{n}
\sin nx\right)\]

利用Parseval等式$$\sum_{n=1}^{\infty}|a_n|^2=\frac{1}{2\pi}\int_{-\pi}^{\pi}x^2dx$$

其中$a_n$为$e^{inx}$的系数，即$\frac{(-1)^n}{n}i$,$a_0=0$

那么有$$2\sum_{k=1}^{\infty}\frac{1}{k^2}=\frac{1}{2\pi}\int_{-\pi}^{\pi}x^2dx$$

可得答案

证明11:傅立叶分析证明

考虑$$f(t)=\sum_{n=1}^{\infty}\frac{\cos{nt}}{n^2}$$
在实轴上一致收敛，对于在$t\in [-\epsilon,2\pi-\epsilon]$,我们有
$$\sum_{n=1}^N\sin{nt}=\frac{e^{it}-e^{i(N+1)t}}{2i(1-e^{it})}+\frac{1-e^{iN)t}}{2i(1-e^{it})}$$
这个和被\[\frac{2}{|1-e^{it}|}=\frac{1}{\sin{t/2}}\]
控制，从而在$[\epsilon,2\pi-\epsilon]$上一致有界，据Dirichlet判别法
\[\sum_{n=1}^{\infty}\frac{\sin{t}}{n}\]
是在$[\epsilon,e\pi-\epsilon]$一致收敛,从而对于$t\in(0,2\pi)$,
$$f'(t)=-\sum_{n=1}^{\infty}\frac{\sin{nt}}{n}=\Im(\log(1-e^{it}))=\arg{(1-e^{it})}=\frac{t-\pi}{2}$$
从而有
$$-\zeta(2)/2-\zeta(2)=f(\pi)-f(0)=\int_0^\pi\frac{t-\pi}{2}dt=-\frac{\pi^2}{4}$$

证明12:泊松公式证明

(Richard Troll)由泊松求和公式$$\sum_{n=-\infty}^{\infty}f(n)=\sum_{k=-\infty}^{\infty}\hat{f}(k)$$可知

其中$\hat{f}(\xi)=\int_{-\infty}^{\infty}f(x) e^{-2\pi ix\xi}dx$为傅立叶变换。

那么有$f(x)=e^{-a|x|}$,$f$的傅立叶变换为

\[\hat{f}(\xi)=\frac{2a}{a^2+4\pi^2\xi^2}\]

也就是说

$$\frac{1}{2a}\sum_{n\in\mathbb{Z}}e^{-a|n|}-\frac{1}{a^2}=\sum_{k=1}^{\infty}\frac{2}{a^2+4\pi^2 k^2}$$

则$$\lim_{a\to 0}\sum_{k=1}^{\infty}\frac{2}{a^2+4\pi^2 k^2}=\lim_{a\to 0}\left\{\frac{1}{2a}\left(\frac{e^a+1}{e^a-1}\right)-\frac{1}{a^2}\right\}=\frac{1}{12}$$

从而就有$\zeta(2)=\frac{\pi^2}{6}$

证明13:概率论证明

(Luigi Pace 发表于2011 American Math Monthly)

设$X_1,X_2$是独立同半区域柯西分布，也就是它们的分布函数都是$p(x)=\frac{2}{\pi(1+x^2)}(x>0)$

令随机变量$Y=X_1/X_2$,那么$Y$的概率密度函数$p_Y$定义在$y>0$，有

\begin{align*}p_Y(y) &= \int_0^{\infty} x p_{X_1} (xy) p_{X_2}(x) dx = \frac{4}{\pi^2} \int_0^\infty \frac{x}{(1+x^2 y^2)(1+x^2)}dx\\
&=\frac{2}{\pi^2 (y^2-1)} \left[\log \left( \frac{1+x^2 y^2}{1+x^2}\right) \right]_{x=0}^{\infty} = \frac{2}{\pi^2} \frac{\log(y^2)}{y^2-1} = \frac{4}{\pi^2} \frac{\log(y)}{y^2-1}.
\end{align*}

由于$X_1,X_2$独立同分布，所以$P(Y>1)=P(X_1>X_2)=1/2$,那么有

$$\frac{1}{2}=\int_0^1\frac{4}{\pi^2}\frac{\log(y)}{y^2-1}dy$$

也就是说

$$\frac{\pi^2}{8} = \int_0^1 \frac{-\log(y)}{1-y^2} dy = -\int_0^1 \log(y) (1+y^2+y^4 + \cdots)  dy = \sum_{k=0}^\infty \frac{1}{(2k+1)^2}$$

那么答案显而易见。

证明14:积分+函数方程证明 

(H Haruki,S Haruki在1983年 American Mathematical Monthly发表)

由于$$\sum_{n=1}^{\infty}\frac{1}{n^2}=\sum_{n=1}^{\infty}\frac{1}{n}\int_0^1 x^{n-1}dx=\int_0^1\frac{\log{(1-x)}}{x}dx$$

只需要算出这个积分值即可，我们令

$$f(a)=\int_0^1\frac{\log{(x^2-2x\cos{a}+1)}}{x}dx$$

要证明$f(a)=-\frac{(a-\pi)^2}{2}+\frac{\pi^2}{6}$

利用等式$(x^2-2x\cos{a}+1)(x^2+2x\cos{a}+1)=x^4-2x^2\cos{2a}+1$我们有

\[f(a/2)+f(\pi-a/2)=\int_0^1\frac{\log{(x^4-2x^2\cos{a}+1)}}{x}=\frac{1}{2}\frac{\log{(t^2-2t\cos{a}+1)}}{t}dt=\frac{1}{2}f(a)\]

中间是令$\sqrt{x}=t$得到的等式。解函数方程$f(a/2)+f(\pi-a/2)=f(a)/2$,求导两次得$f''(a/2)+f''(\pi-a/2)=2f''(a)$,由于$f''$是在闭区间$[0,2\pi]$上的连续函数，从而$f''$在该区域有最大值$M$与最小值$m$.设$f''(a_0)=M$对于某个$a_0\in[0,2\pi]$成立，在等式中设$a=a_0$有

\[f''(a_0/2)+f''(\pi-a_0/2)=2f''(a_0)=2M\]
但是由于$f''(a_0/2),f''(\pi-a_0/2)$都小于$M$,从而只能都等于$M$.继续这样的迭代，就有
\[\lim_{n\to\infty} f''(a_0/2^n)=f''(0)=M\]
类似地，我们就有$f''(0)=m$,从而$M=m$,$f''$为常函数，则$f$只能是二次函数，设
\[f(a)=\alpha \frac{a^2}{2}+\beta a+\gamma\]
代入式子有$-\pi\alpha/2=\beta/2,\pi^2\alpha/2+\beta\pi+2\gamma=\gamma/2$,而
$$f'(a)=\int_0^1\frac{2\sin{a}}{1+x^2-2x\cos{a}}dx$$
得知$f'(\pi/2)=\pi/2$
从而有$\alpha=-1,\beta=\pi,\gamma=-\pi^2/3$,代入$a=0$,得到$$\int_0^1\frac{\log{(1-x)}}{x}dx=-\frac{\pi^2}{6}$$

证明15:三角恒等式的初等证明

(Josef Hofbauer发表于2002年American Mathematical Monthly)

$$\frac{1}{\sin^2x}=\frac{1}{4\sin^2{\frac{x}{2}}\cos^2{\frac{x}{2}}}=\frac{1}{4}\left[\frac{1}{\sin^2{\frac{x}{2}}}+\frac{1}{\sin^2{\frac{\pi+x}{2}}}\right]$$
从而就有
$$1=\frac{1}{\sin^2{\frac{\pi}{2}}}=\frac{1}{4\left[\frac{1}{\sin^2{\frac{\pi}{4}}}+\frac{1}{\sin^2{\frac{3\pi}{4}}}\right]}=\cdots =\frac{1}{4^n}\sum_{k=0}^{2^n-1}\frac{1}{\sin^2{\frac{(2k+1)\pi}{2^{n+1}}}}=\frac{2}{4^n}\sum_{k=0}^{2^{n-1}-1}\frac{1}{\sin^2{\frac{(2k+1)\pi}{2^{n+1}}}}$$

又由于$\sin^{-2}x>x^{-2}>\tan^{-2}x$对$x\in(0,\pi/2)$成立

令$x=(2k+1)\pi/(2N)$,对$k=0,1,\cdots,N/2-1(N=2^n)$对不等式求和，就变为
$$1>\frac{8}{\pi^2}\sum_{k=0}^{2^n-1}\frac{1}{(2k+1)^2}>1-\frac{1}{N}$$
令$N\to\infty$可得答案

证明16:三角多项式的证明

(Kortram发表于1996年 Mathematics Magazine)

对于奇数$n=2m+1$,我们知道$\sin{nx}=F_n(\sin{x})$,其中$F_n$是次数$n$的多项式。那么$F_n$的零点为$\sin(j\pi/n)(-m\le j\le m)$,且有$\lim_{y\to 0}(F_n(y)/y)=n$.那么
$$F_n(y)=ny\prod_{j=1}^m\left(1-\frac{y^2}{\sin^2(j\pi/n)}\right)$$
从而
$$\sin{nx}=n\sin{x}\prod_{j=1}^m\left(1-\frac{\sin^2x}{\sin^2(j\pi/n)}\right)$$
比较两边泰勒展开的$x^3$系数，有
\[-\frac{n^3}{6}=-\frac{n}{6}-n\sum_{j=1}^{m}\frac{1}{\sin^2(j\pi/n)}\]
于是$$\frac{1}{6}-\sum_{j=1}^m\frac{1}{n^2\sin^2(j\pi/n)}=\frac{1}{6n^2}$$
固定整数$M$,令$m>M$,则有
$$\frac{1}{6}-\sum_{j=1}^M\frac{1}{n^2\sin^2(j\pi/n)}=\frac{1}{6n^2}+\sum_{j=M+1}^m\frac{1}{n^2\sin^2(j\pi/n)}$$
利用$\sin{x}>\frac{2}{\pi}x$对于$0<x<\frac{\pi}{2}$成立，我们有
$$0<\frac{1}{6}-\sum_{j=1}^M\frac{1}{n^2\sin^2(j\pi/n)}=\frac{1}{6n^2}+\sum_{j=M+1}^m\frac{1}{4j^2}$$
令$n,m$趋于无穷，就有
$$0\le \frac{1}{6}-\sum_{j=1}^M\frac{1}{\pi^2j^2}\le \sum_{j=M+1}^m\frac{1}{4j^2}$$
也即$$\sum_{j=1}^{\infty}\frac{1}{\pi^2j^2}=\frac{1}{6}$$

证明17:积分证明

(Matsuoka发表于1961年American Mathematical Montly)

考虑积分
$$I_n=\int_0^{\pi/2}\cos^{2n}xdx\mbox{ and }J_n=\int_0^{\pi/2}x^2\cos^{2n}xdx$$
我们有Wallis公式：
$$I_n=\frac{1\cdot 3\cdot 5\cdots (2n-1)}{2\cdot 4\cdot 6\cdots 2n}\frac{\pi}{2}=\frac{(2n)!}{4^n(n!)^2}\frac{\pi}{2}$$
那么对于$n>0$,分部积分有
\begin{align*}
I_n&=[x\cos^{2n}x]_0^{\pi/2}+2n\int_0^{\pi/2}x\sin{x}\cos^{2n-1}xdx\\
&=n(2n-1)J_{n-1}-2n^2 J_n
\end{align*}
从而有$$\frac{(2n)!}{4^n(n!)^2}\frac{\pi}{2}=n(2n-1)J_{n-1}-2n^2 J_n$$
得到$$\frac{\pi}{4n^2}=\frac{4^{n-1}(n-1)!^2}{(2n-2)!}J_{n-1}-\frac{4^nn!^2}{(2n)!}J_n$$
将这个式子从1加到$n$，能够有
\[\frac{\pi}{4}\sum_{n=1}^N\frac{1}{n^2}=J_0-\frac{4^N N!^2}{(2N)!}J_N\]
由于$J_0=\pi^3/24$,只需要证明$\lim_{N\to\infty} 4^N N!^2 J_N/(2N)!=0$,但是不等式$x<\frac{\pi}{2}\sin{x}$对于$0<x<\frac{\pi}{2}$,得到
$$J_N<\frac{\pi^2}{4}\int_0^{\pi/2}\sin^2x\cos^{2N}xdx=\frac{\pi^2}{4}(I_N-I_{N+1})=\frac{\pi^2 I_N}{8(N+1)}$$
也即$$0<\frac{4^N N!^2}{(2N)!}J_N<\frac{\pi^3}{16(N+1)}$$

证明18:Fejér核的证明

(Stark在1969年American Mathematical Monthly上的证明)

对于Fejér核有如下等式：
\[\left(\frac{\sin{nx/2}}{\sin{x/2}}\right)^2=\sum_{k=-n}^n(n-|k|)e^{ikx}=n+2\sum_{k=1}^n(n-k)\cos{kx}\]
故而有
\begin{align*}
\int_0^\pi x\left(\frac{\sin{nx/2}}{\sin{x/2}}\right)^2 &= \frac{n\pi^2}{2}+2\sum_{k=1}^n(n-k)\int_0^\pi x\cos{kx}dx \\
&=\frac{n\pi^2}{2}-2\sum_{k=1}^n(n-k)\frac{1-(-1)^k}{k^2}\\
&=\frac{n\pi^2}{2}-4n\sum_{1\le k\le n,2\nmid k}\frac{1}{k^2}+4\sum_{1\le k\le n,2\nmid k}\frac{1}{k}
\end{align*}
如果我们令$n=2N,N\in\mathbb{Z^+}$,那么
$$\int_0^\pi \frac{x}{8N}\left(\frac{\sin{Nx}}{\sin{x/2}}\right)^2dx=\frac{\pi^2}{8}-\sum_{r=0}^{N-1}\frac{1}{(2r+1)^2}+O\left(\frac{\log{N}}{N}\right)$$
但是由于$\sin{x/2}>x/\pi$对于$0<x<\pi$成立，那么
$$\int_0^\pi \frac{x}{8N}\left(\frac{\sin{Nx}}{\sin{x/2}}\right)^2dx < \frac{\pi^2}{8N}\int_0^\pi \sin^2Nx \frac{dx}{x}=\frac{\pi^2}{8N}\int_0^{N\pi} \sin^2y \frac{dy}{y}=O\left(\frac{\log{N}}{N}\right)$$
也即$$\frac{\pi^2}{8}=\sum_{r=0}^{\infty}\frac{1}{(2r+1)^2}$$

证明19:Gregory定理证明

证明来自Borwein & Borwein的著作"Pi and the AGM"

以下公式是著名的Gregory定理：

$$\frac{\pi}{4}=\sum_{n=0}^{\infty}\frac{(-1)^n}{2n+1}$$

令$$a_N=\sum_{n=-N}^N\frac{(-1)^n}{2n+1},b_N=\sum_{n=-N}^N\frac{1}{(2n+1)^2}$$

我们需要证明$\lim_{N\to\infty} a_N^2-b_N=0$即可

如果$n\not = m$那么
$$\frac{1}{(2n+1)(2m+1)}=\frac{1}{2(m-n)}\left(\frac{1}{2n+1}-\frac{1}{2m+1}\right)$$
就有
\begin{align*}
a_N^2-b_N&=\sum_{n=-N}^N\sum_{m=-N,m\not = n}^N\frac{(-1)^{m+n}}{2(m-n)}\left(\frac{1}{2n+1}-\frac{1}{2m+1}\right)\\
&=\sum_{n=-N}^N\sum_{m=-N,m\not = n}^N\frac{(-1)^{m+n}}{(m-n)}\frac{1}{(m-n)(2n+1)}=\sum_{n=-N}^N\frac{(-1)^n c_{n,N}}{2n+1}
\end{align*}
其中\[c_{n,N}=\sum_{m=-N,m\not=n}^N\frac{(-1)^m}{m-n}\]
很容易可见$c_{-n,N}=-c_{n,N}$,故而$c_{0,N}=0$若$n>0$那么
\[c_{n,N}=(-1)^{n+1}\sum_{j=N-n+1}^{N+n}\frac{(-1)^j}{j}\]
我们可以知道$|c_{n,N}|\le1/(N-n+1)$由于这个交错和加了后比第一项要小，也即
\begin{align*}|a_N^2-b_N|&\le \sum \left(\frac{1}{(2n-1)(N-n+1)}+\frac{1}{(2n+1)(N-n+1)}\right)\\
&=\sum_{n=1}^N\frac{1}{2N+1}\left(\frac{2}{2n-1}+\frac{1}{N-n+1}\right)+\sum_{n=1}^N\frac{1}{2N+3}\left(\frac{2}{2n+1}+\frac{1}{N-n+1}\right)\\
&\le \frac{1}{2N+1}(2+4\log{(2N+1)}+2+2\log{(N+1)})
\end{align*}
所以$a_N^2-b_N$趋于$0$成立。

证明20:数论的证明

(本证明来自华罗庚的数论)

需要用到整数能被表示为四个平方的和。令$r(n)$为四元组使得$n=x^2+y^2+z^2+t^2$成立的四元组$(x,y,z,t)$的个数。最平凡的是$r(0)=1$,同时，我们知道
\[r(n)=8\sum_{m|n,4\nmid m}m\]
对于$n>0$成立。令$R(N)=\sum_{n=0}^N r(n)$,很容易可以看出，$R(N)$是渐进于半径$\sqrt{N}$的四维球体积。也即$R(N)\sim \frac{\pi^2}{2}N$.但是
\[R(N)=1+8\sum_{n=1}^N\sum_{m|n,4\nmid m}m=1+8\sum_{m\le N,4\nmid m}m\left\lfloor \frac{N}{m}\right\rfloor = 1+8(\theta(N)-4\theta(N/4))\]
其中\[\theta(x)=\sum_{m\le x}m\left\lfloor \frac{x}{m}\right\rfloor\]
但是
\begin{align*}\theta(x)&=\sum_{mr\le x}m=\sum_{r\le x}\sum_{m=1}^{\lfloor x/r \rfloor}m=\frac{1}{2}\sum_{r \le x}\left(\left\lfloor\frac{x}{r}\right\rfloor^2+\left\lfloor\frac{x}{r}\right\rfloor\right)=\frac{1}{2}\sum_{r \le x}\left(\left\lfloor\frac{x}{r}\right\rfloor^2+O\left(\frac{x}{r}\right)\right)\\
&=\frac{x^2}{2}(\zeta(2)+O(1/x))+O(x\log{x})=\frac{\zeta(2) x^2}{2}+O(x\log{x})
\end{align*}
当$x\to\infty$成立，从而
\[R(N)\sim \frac{\pi^2}{2}N^2\sim 4\zeta(2)\left(N^2-\frac{N^2}{4}\right)\]
得到$\zeta(2)=\pi^2/6$

证明21:类似的初等证明

首先我们要证明这个等式：

\[\sum_{k=1}^n \cot^2 \left( \frac {2k-1}{2n} \frac{\pi}{2} \right) = 2n^2 – n\]

是由于注意到

\[\cos 2n\theta = \text{Re}(\cos\theta + i \sin\theta)^{2n} = \sum_{k=0}^n (-1)^k {2n \choose 2k}\cos^{2n-2k}\theta\sin^{2k}\theta\]

就立即可得

\[\frac{\cos 2n\theta}{\sin^{2n}\theta} =  \sum_{k=0}^n (-1)^k {2n \choose 2k}\cot^{2n-2k}\theta\]

令$x=\cot^2{\theta}$,就可以变为

\[f(x) = \sum_{k=0}^n (-1)^k {2n \choose 2k}x^{n-k}\]

有根$x_j = \cot^2 (2j-1)\pi/4n$对$j=1,2,\cdots ,n$成立，从而由于$\binom{2n}{2n-2}=2n^2-n$,韦达定理知答案。

有了这个等式，我们类似初等证明中的方法进行证明

现在$1/\theta > \cot \theta > 1/\theta - \theta/3 > 0$对于$0< \theta< \pi/2 < \sqrt{3}$成立，就有
\[1/\theta^2 – 2/3 < \cot^2 \theta < 1/\theta^2\]
对于$\theta_k = (2k-1)\pi/4n$做和，从$k=1$到$n$我们得到
$$2n^2 – n < \sum_{k=1}^n \left( \frac{2n}{2k-1}\frac{2}{\pi} \right)^2 < 2n^2 – n + 2n/3$$
从而有\[\frac{\pi^2}{16}\frac{2n^2-n}{n^2} < \sum_{k=1}^n \frac{1}{(2k-1)^2} <
\frac{\pi^2}{16}\frac{2n^2-n/3}{n^2}\]
这也就是我们想要的
$$\sum_{k=1}^\infty \frac{1}{(2k-1)^2} = \frac{\pi^2}{8}$$

证明22:伯努利数的证明

函数$B(x) = \frac{x}{e^x - 1}$为伯努力数$B_k$的生成函数，有$B$是亚纯，且只在$2\pi in$有极点，利用Mittag-Leffler定理可以展开为

$$\frac{x}{e^x - 1} = \sum_{n \in \mathbb{Z}} \frac{2\pi i n}{x - 2 \pi i n} = \sum_{n \in \mathbb{Z}} - \left( \frac{1}{1 - \frac{x}{2\pi i n}} \right).$$

而注意到后者又可以展开为几何级数相加：

\[\frac{x}{e^x - 1} = - \sum_{n \in \mathbb{Z}} \sum_{k \ge 0} \left( \frac{x}{2\pi i n} \right)^k = \sum_{k \ge 0} (-1)^{n+1} \frac{2 \zeta(2n)}{(2\pi )^{2n}} x^{2n}\]

是由于在重排级数的同时，奇数项消去了而偶数项留下了，所以我们就得到如下式子：

$$B_{2n} = (-1)^{n+1} \frac{2 \zeta(2n)}{(2\pi)^{2n}}$$

也就是要求计算

$$B_2=\lim_{x\to 0}\frac{1}{x^2}\left\{\frac{x}{e^x - 1}-1+\frac{x}{2}\right\}=\frac{1}{12}$$

那么$\zeta(2)=\pi^2/6$就能得到了。

证明23:超几何正切分布的证明

（本证明来自Lars Holst于2013年Journal of Applied Probability的证明）

注意到超几何正切函数$f_1(x)=\frac{2}{\pi(e^x-e^{-x})}$,有\[\int_{-\infty}^x\frac{2}{\pi (e^y-e^{-y})}dy=\frac{2}{\pi}\arctan(e^x).\]

这样可以知道$f_1$是一个分布函数，而如果$X_1,X_2$都满足超几何正切分布的话，我们有如下引理：

$X_1+X_2$的概率密度是：\[f_2(x)=\frac{4x}{\pi^2(e^x-e^{-x})}.\]

这是因为

\begin{align*}
\int_{-\infty}^\infty &\frac{2}{\pi(e^y+e^{-y})} \frac{2}{\pi(e^{x-y}+e^{y-x})}dy\\
&=\frac{4}{\pi^2}\int_0^\infty \frac{u e^{-x}}{(1+u^2)(1+u^2 e^{-2x})}du\\
&= \frac{4}{\pi(e^x-e^{-x})}\int_0^\infty \left(\frac{u}{1+u^2}-\frac{u e^{-2x}}{1+u^2 e^{-2x}}\right)du \\&=\frac{4 x}{\pi(e^x-e^{-x})}
\end{align*}
而知道这样的函数是密度函数之后，我们就可以得到Basel问题：

\begin{align*}\sum_{k=0}^{\infty} \frac{1}{(2k+1)^2} &=\sum_{k=0}^\infty \int_0^\infty x e^{-(2k+1)x}dx \\
&=\int_0^\infty x e^{-x} \sum_{k=0}^{\infty} e^{-2kx}dx=\int_0^\infty \frac{x e^{-x}}{1-e^{-2x}}dx\\
&=\frac{\pi^2}{8}\int_{-\infty}^\infty f_2(x)dx=\frac{\pi^2}{8}
\end{align*}

这样可以得到结论。

Reference：

[1]Robin Chapman "Evaluating $\zeta(2)$"

（未完待续..）