浏览器输入一个url的过程，以及加载完html文件和js文件的标志

简单理解：

当在浏览器地址栏输入一url时，浏览器会做以下几个步骤：

1、将url转化为ip地址，也就是DNS解析，（先找本地host文件中是否有对应的ip地址，如果有就直接用，没有的话，就按域名的二级，一级的顺序进行查找）。

2、找到请求的的服务器后，就开始建立tcp连接，此处有三次握手。

3、tcp建立连接后，开始向服务器发送请求，服务器首先响应并返回的是一个html文档。

4、此处就是浏览器解析html文档了，

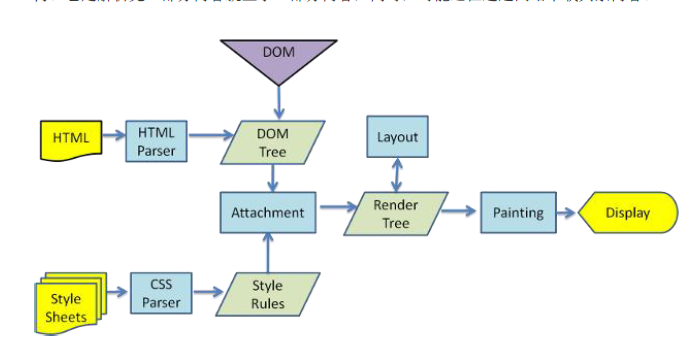
解析html文档，就是按照html文档标签的顺序，从上往下进行解析，并在这个过程中构建dom树(dom tree)，

如果遇到css文件，则向服务器请求加载css文件，并解析，构建css规则树（css rule tree）,

解析过程中，如果遇到需要加载js文件，则会阻塞dom树和css规则树的构建，

因为js中有修改dom,以及css样式的代码（所以，一般情况下，是将js文件放在body最下方，防止构建dom树时被阻塞）(此处说一下，js文件加载完成的标志是window.onload事件)

dom树构建完成的标志是，监听DomContentLoaded事件

然后根据dom树和css rule tree一起构建 渲染树（render tree）。

然后根据render tree 进行布局（layout）,然后进行绘制painting

//此处是一个完整的，解决兼容的判断js文件加载完成的标志
function loadJsAsync(url){
    var body = document.getElementsByTagName('body')[0];
    var jsNode = document.createElement('script');

    jsNode.setAttribute('type', 'text/javascript');
    jsNode.setAttribute('src', url);
    body.appendChild(jsNode);

    if (jsNode.onload) {
        jsNode.onload = function() {
            // do something
        }
    } else {
        // ie6, ie7不支持onload的情况
        jsNode.onreadystatechange = function() {
            if(jsNode.readyState == 'loaded' || jsNode.readyState == 'complete') {
                // 异步js加载完毕
                // do something执行操作
            }
        }
    }
}

参考文章：https://www.cnblogs.com/ranyonsue/p/6734446.html， http://blog.csdn.net/xiaobing_hope/article/details/78318471

加深理解：

按照浏览器引擎的渲染机制理解。

浏览器的每一个tab页都是打开一个新的进程

而每一个进程都是由多个线程所组成。

所以每一个浏览器tab页都是有：主进程，而主进程包含浏览器渲染引擎、浏览器数据存储

浏览器渲染引擎由以下多个线程组成：定时器线程、事件处理线程、异步http请求线程、js解析，ui渲染（与js解析互斥）

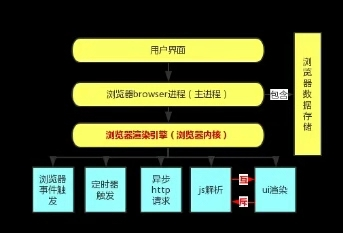
所以js的加载会阻塞页面的渲染。

js判断页面当前实在手机端还是pc端

if(/(iPhone|iPad|iPod|iOS|Android)/i.test(navigator.userAgent)){

}

此文是按本人的理解写的，如有路过的大神，看到有不合理的地方，谢谢指正！