我理解的数据结构（三）—— 队列（Queue）

我理解的数据结构（三）—— 队列（Queue）

一、队列

• 队列是一种线性结构
• 相比数组，队列对应的操作是数组的子集
• 只能从一端（队尾）添加元素，只能从另一端（队首）取出元素
• 队列是一种先进先出的数据结构（FIFO）

二、数组队列与循环队列

1. 数组队列

如果你有看过我之前的文章不要小看了数组或者栈，你就会发现，自己封装一个数组队列是如此的轻松加愉快！

（1）先定义一个接口，接口中定义队列需要实现的方法

```
public interface Queue<E> {
int getSize();
boolean isEmpty();
// 查看队首元素
E getFront();
// 入队
void enqueue(E ele);
// 出队
E dequeue();
}
```

（2）实现数组队列

```
public class ArrayQueue<E> implements Queue<E> {

// 这里的数组是在之前的文章中封装好的，直接拿来用就好了
private ArrayNew<E> array;

public ArrayQueue(int capacity) {
    array = new ArrayNew<>(capacity);
}

public ArrayQueue() {
    this(10);
}

public int getCapacity() {
    return array.getCapacity();
}

@Override
public int getSize() {
    return array.getSize();
}

@Override
public boolean isEmpty() {
    return array.isEmpty();
}

@Override
public E getFront() {
    return array.getFirst();
}

@Override
public void enqueue(E ele) {
    array.addLast(ele);
}

@Override
public E dequeue() {
    return array.removeFirst();
}

@Override
public String toString() {

    StringBuffer res = new StringBuffer();

    res.append(String.format("arrayQueue: size = %d, capacity = %d\n", getSize(), getCapacity()));
    res.append("front [");

    for (int i = 0; i < array.getSize(); i++) {
        res.append(array.get(i));
        if (i != getSize() - 1) {
            res.append(", ");
        }
    }
    res.append("] tail");
    return res.toString();

}

}

<p><strong>（3）数组队列的复杂度</strong></p>
<table>
<thead><tr>
<th align="center">方法</th>
<th align="center">复杂度</th>
</tr></thead>
<tbody>
<tr>
<td align="center"><code>enqueue</code></td>
<td align="center">O(1) 均摊</td>
</tr>
<tr>
<td align="center"><code>dequeue</code></td>
<td align="center">O(n)</td>
</tr>
<tr>
<td align="center"><code>front</code></td>
<td align="center">O(1)</td>
</tr>
<tr>
<td align="center"><code>getSize</code></td>
<td align="center">O(1)</td>
</tr>
<tr>
<td align="center"><code>isEmpty</code></td>
<td align="center">O(1)</td>
</tr>
</tbody>
</table>
<blockquote>这个时候我们会发现，在进行出队操作的时候，数组队列的复杂度是0(n)，如果我们频繁的进行出队操作，那么其实数组队列的效率是很低的，如何提升数组队列的性能呢？这个时候我们就要用到循环队列了。</blockquote>
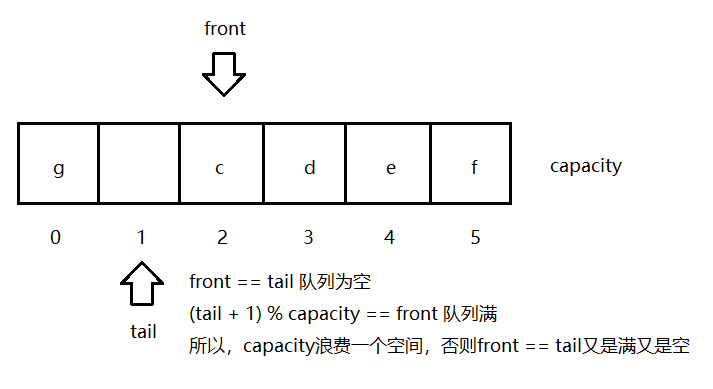
<h4>2. 循环队列队列</h4>
<blockquote>循环队列的原理：</blockquote>
<ol>
<li>
<code>dequeue</code>时，不要在去除队首元素时，把整体向前移动</li>
<li>维护 <code>front</code> 、 <code>tail</code> 和 <code>size</code> 这三个属性</li>
<li>
<code>enqueue</code>的时候<code>tail++</code>
</li>
<li>
<code>dequeue</code>的时候<code>front++</code>
</li>
</ol>

![](https://img2018.cnblogs.com/blog/1504257/201811/1504257-20181117135616157-1981589685.png)

<p><strong>（1）实现循环队列</strong></p>

public class LoopQueue<E> implements Queue<E> {

private E[] array;
private int size;
private int front;
private int tail;

public LoopQueue(int capacity) {
    // 我们需要浪费一个空间去判断队列是否已满，所以需要把capacity + 1
    array = (E[])new Object[capacity + 1];
    front = 0;
    tail = 0;
    size = 0;
}

public LoopQueue() {
    this(10);
}

// 返回用户传递的队列大小
public int getCapacity() {
    return array.length - 1;
}

@Override
public int getSize() {
    return size;
}

@Override
public boolean isEmpty() {
    return front == tail;
}

@Override
public E getFront() {
    if (isEmpty()) {
        throw new IllegalArgumentException("Queue is empty. Can't get front.");
    }

    return array[0];
}

@Override
public void enqueue(E ele) {

    if (front == (tail + 1) % array.length) {
        // 扩展队列长度为原长度2倍
        resize(getCapacity() * 2);
    }

    array[tail] = ele;
    size++;
    tail = (tail + 1) % array.length;
}

@Override
public E dequeue() {

    if (isEmpty()) { // 队列为空
        throw new IllegalArgumentException("Queue is empty. Can't get dequeue.");
    }

    E ele = array[front];

    size--;
    array[front] = null;
    front = (front + 1) % array.length;

    if (size == getCapacity() / 4 && getCapacity() / 2 != 0) {
        resize(getCapacity() / 2);
    }

    return ele;

}

private void resize(int newCapacity) {
    E[] newArray = (E[]) new Object[newCapacity + 1];

    for (int i = 0; i < size; i++) {
        newArray[i] = array[(front + i) % array.length];
    }

    array = newArray;
    front = 0;
    tail = size;
}

@Override
public String toString() {
    StringBuffer res = new StringBuffer();

    res.append(String.format("queue: size = %d, capacity = %d\n", getSize(), getCapacity()));
    res.append("front [");

    // 循环条件，和循环增量都要注意下
    for (int i = front; i != tail; i = (i + 1) % array.length) {
        res.append(array[i]);

        if ((i + 1) % array.length != tail) {
            res.append(", ");
        }
    }
    res.append("] tail");

    return res.toString();
}

}

<p><strong>（2）循环队列的复杂度</strong></p>
<table>
<thead><tr>
<th align="center">方法</th>
<th align="center">复杂度</th>
</tr></thead>
<tbody>
<tr>
<td align="center"><code>enqueue</code></td>
<td align="center">O(1) 均摊</td>
</tr>
<tr>
<td align="center"><code>dequeue</code></td>
<td align="center">O(1) 均摊</td>
</tr>
<tr>
<td align="center"><code>front</code></td>
<td align="center">O(1)</td>
</tr>
<tr>
<td align="center"><code>getSize</code></td>
<td align="center">O(1)</td>
</tr>
<tr>
<td align="center"><code>isEmpty</code></td>
<td align="center">O(1)</td>
</tr>
</tbody>
</table>
<h3>三、用时间说话</h3>
<p><strong>（1）用时方法</strong></p>

public static double test(Queue<Integer> q, int opCount) {

// 纳秒
long startTime = System.nanoTime();

Random random = new Random();

for (int i = 0; i < opCount; i++) {
    q.enqueue(random.nextInt(Integer.MAX_VALUE));
}
for (int i = 0; i < opCount; i++) {
    q.dequeue();
}

// 纳秒
long endTime = System.nanoTime();

return (endTime - startTime) / 1000000000.0;

}

<p><strong>（2）调用</strong></p>

// 十万次入队和十万次出队操作

int opCount = 100000;

ArrayQueue<Integer> aq = new ArrayQueue<>();

double time1 = test(aq, opCount);

System.out.println(time1);

LoopQueue<Integer> lq = new LoopQueue<>();

double time2 = test(lq, opCount);

System.out.println(time2);

<p><strong>（3）结果</strong></p>
<ul>
<li>14.635995113</li>
<li>0.054536447</li>
</ul>
<blockquote>这个就是算法和数据结构的力量！</blockquote>

原文地址：https://segmentfault.com/a/1190000016147024