[HNOI2008]水平可见直线 单调栈

题目描述：
在xoy直角坐标平面上有n条直线L1,L2,...Ln,若在y值为正无穷大处往下看,能见到Li的某个子线段,则称Li为
可见的,否则Li为被覆盖的.
例如,对于直线:
L1:y=x; L2:y=-x; L3:y=0
则L1和L2是可见的,L3是被覆盖的.
给出n条直线,表示成y=Ax+B的形式(|A|,|B|<=500000),且n条直线两两不重合.求出所有可见的直线.

题解：

一道很好的思维题。
1.简单手画一下，能被看到的直线应该是所有直线一起围成的大凸包。
2.由于是凸包，我们考虑将所有直线按斜率排序，从小到大依次加入到平面直角坐标系中。
3.我们考虑一下新加入直线的情况：

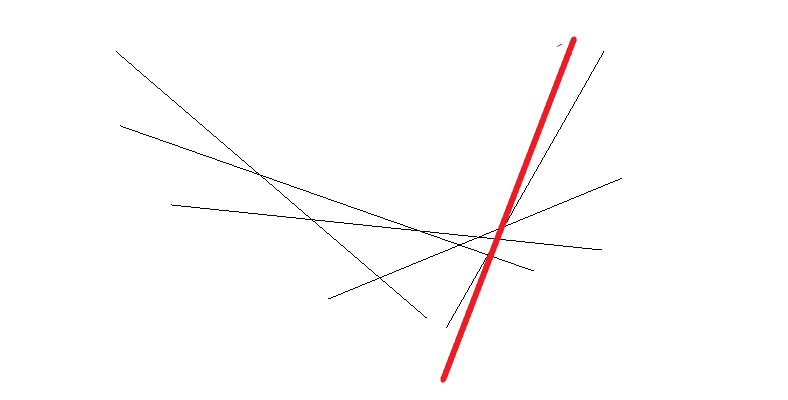
在这种情况中，我们可以看到新加入的红色直线与加入之前平面中斜率第二大的直线的交点位于先前第一大与第二大之左，显然，这就会挡住平面中斜率第二大的直线，我们就将该直线弹出，直到找到一个交点在新加入直线的交点左侧。
对于整个过程，直线的斜率单调递增，交点横坐标也单调递增，直接用单调栈维护即可。
时间复杂度为 $O(n)$

Code:

#include<cstdio>
#include<algorithm>
#include<string>
using namespace std;
void setIO(string a){
	freopen((a+".in").c_str(),"r",stdin);
}
const int maxn=100000+5;
struct Line{
	double slope, y;
}line[maxn];
int arr[maxn],ans[maxn],S[maxn],top;
bool cmp(int i,int j){
	if(line[i].slope==line[j].slope) return line[i].y>line[j].y;
	return line[i].slope<line[j].slope;
}
double get(int i,int j){
	return (line[i].y-line[j].y)/(line[j].slope-line[i].slope);
}
int main(){
	//setIO("input");
	int n;
	scanf("%d",&n);
	for(int i=1;i<=n;++i) {
		scanf("%lf%lf",&line[i].slope,&line[i].y);
		arr[i]=i;
	}
	sort(arr+1,arr+1+n,cmp);
    for(int i=1;i<=n;++i)
    {
    	int cur=arr[i];

    	if(line[cur].slope==line[arr[i-1]].slope && i!=1) continue;
    	while(top>1 && get(S[top],S[top-1])>=get(arr[i],S[top])) --top;
    	S[++top]=cur;
    	ans[top]=cur;
    }
    sort(ans+1,ans+1+top);
    for(int i=1;i<=top;++i) printf("%d ",ans[i]);
    return 0;
}