OpenCV 之 透视 n 点问题

透视 n 点问题，源自相机标定，是计算机视觉的经典问题，广泛应用在机器人定位、SLAM、AR/VR、摄影测量等领域

1  PnP 问题

1.1  定义

已知：相机的内参和畸变系数；世界坐标系中，n 个空间点坐标，以及投影在像平面上的像素坐标

求解：相机在世界坐标系下的位姿 R 和 t，即 {W} 到 {C} 的变换矩阵 $\;^w_c\bm{T} $，如下图：

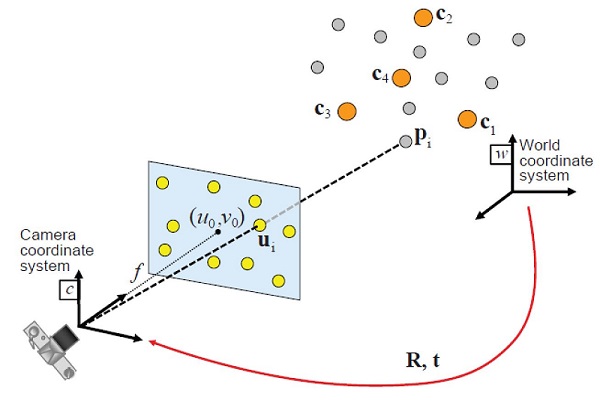
世界坐标系中的 3d 空间点，与投影到像平面的 2d 像素点，两者之间的关系为：

$\quad s \begin{bmatrix} u \\ v \\ 1 \end{bmatrix}  = \begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix}  \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_1 \\ r_{21} & r_{22} & r_{23} & t_2 \\ r_{31} & r_{32} & r_{33} & t_3 \end{bmatrix}  \begin{bmatrix} X_w \\ Y_w \\ Z_w\\ 1 \end{bmatrix} $

1.2  分类

根据给定空间点的数量，可将 PnP 问题分为两类：

第一类  3≤n≤5，选取的空间点较少，可通过联立方程组的方式求解，精度易受图像噪声影响，鲁棒性较差

第二类  n≥6，选取的空间点较多，可转化为求解超定方程的问题，一般侧重于鲁棒性和实时性的平衡

2  求解方法

2.1  DLT 法

2.1.1  转化为 Ax=0

令 $P = K\;[R\;\, t]$，$K$ 为相机内参矩阵，则 PnP 问题可简化为：已知 n 组 3d-2d 对应点，求解 $P_{3\times4}$

DLT (Direct Linear Transformation，直接线性变换)，便是直接利用这 n 组对应点，构建线性方程组来求解

$\quad s \begin{bmatrix} u \\ v \\ 1 \end{bmatrix}  =  \begin{bmatrix} p_{11} & p_{12} & p_{13} & p_{14} \\ p_{21} & p_{22} & p_{23} & p_{23} \\ p_{31} & p_{32} & p_{33} & p_{33} \end{bmatrix}  \begin{bmatrix} X_w \\ Y_w \\ Z_w\\ 1 \end{bmatrix} $

简化符号 $X_w, Y_w, Z_w$ 为 $X, Y, Z$，展开得：

$\quad \begin{equation}  \begin{cases}  su= p_{11}X + p_{12}Y + p_{13}Z + p_{14}\\ \\sv=p_{21}X + p_{22}Y + p_{23}Z + p_{24} \\ \\s\;=p_{31}X + p_{32}Y + p_{33}Z + p_{34}  \end{cases}\end{equation} \;\bm{=>} \; \begin{cases}  Xp_{11} + Yp_{12} + Zp_{13} + p_{14} - uXp_{31} - uYp_{32} - uZp_{33} - up_{34} = 0 \\ \\ Xp_{21} + Yp_{22} + Zp_{23} + p_{24} - vXp_{31} - vYp_{32} - vZp_{33} - vp_{34} = 0 \end{cases}$

未知数有 11 个 ($p_{34}$可约掉)，则至少需要 6 组对应点，写成矩阵形式如下：

$\quad \begin{bmatrix} X_1&Y_1&Z_1&1 &0&0&0&0&-u_1X_1&-u_1Y_1&-u_1Z_1&-u_1 \\ 0&0&0&0& X_1&Y_1&Z_1&1&-v_1X_1&-v_1Y_1&-v_1Z_1&-v_1 \\ \vdots &\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots \\ \vdots &\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\ X_n&Y_n&Z_n&1 &0&0&0&0&-u_nX_n&-u_nY_1&-u_nZ_n&-u_n \\ 0&0&0&0& X_n&Y_n&Z_n&1&-v_nX_n&-v_nY_n&-v_nZ_n&-v_n\end{bmatrix} \begin{bmatrix}p_{11}\\p_{12}\\p_{13}\\p_{14}\\ \vdots\\p_{32}\\p_{33}\\p_{34}\end{bmatrix}=\begin{bmatrix}0\\ \vdots\\ \vdots\\0\end{bmatrix}$

因此，求解 $P_{3\times4}$ 便转化成了 $Ax=0$ 的问题

2.1.2  SVD 求 R t

给定相机内参矩阵，则有  $K \begin{bmatrix} R & t \end{bmatrix} = \lambda \begin{bmatrix} p_1 & p_2 &p_3&p_4 \end{bmatrix}$

考虑 $\lambda$ 符号无关，得  $\lambda R = K^{-1}\begin{bmatrix} p_1 & p_2&p_3 \end{bmatrix}$

SVD 分解  $K^{-1}\begin{bmatrix} p_1&p_2&p_3\end{bmatrix}=\bm{U}\begin{bmatrix}d_{11} && \\ &d_{22}&\\&&&d_{33}\end{bmatrix} \bm{V^T}$

$\quad=> \lambda \approx d_{11}$  和  $\begin{cases}\bm{R=UV^T} \\ \bm{t=\dfrac{K^{-1}p_4}{d_{11}}} \end{cases}$

2.2  P3P 法

当 n=3 时，PnP 即为 P3P，它有 4 个可能的解，求解方法是 余弦定理 + 向量点积

2.2.1  余弦定理

根据投影几何的消隐点和消隐线，构建 3d-2d 之间的几何关系，如下：

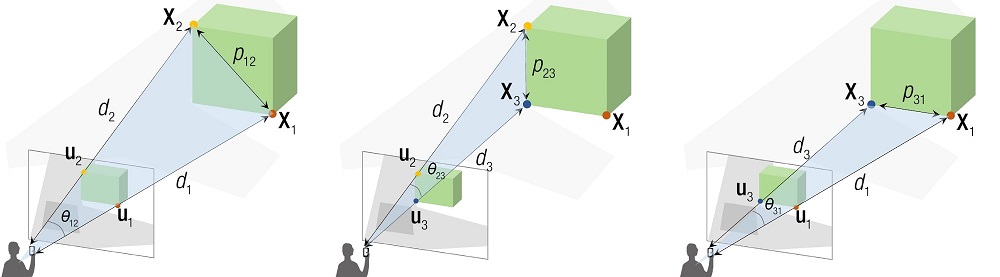
根据余弦定理，则有

$\begin{cases} d_1^2 + d_2^2 - 2d_1d_2\cos\theta_{12} = p_{12}^2  \\ \\ d_2^2 + d_3^2 - 2d_2d_3\cos\theta_{23} = p_{23}^2 \\ \\ d_3^2 + d_1^2 + 2d_3d_2\cos\theta_23 = p_{31}^2 \end{cases}$

其中，只有 $d_1,\, d_2,\,d_3$ 是未知数，求解方程组即可

有个隐含的关键点：给定相机内参，以及 3d-2d 的投影关系，则消隐线之间的夹角 $\theta_{12}\; \theta_{23}\; \theta_{31}$ 是可计算得出的

2.2.2  向量点积

相机坐标系中，原点即为消隐点，原点到 3d-2d 的连线即为消隐线，如图所示：

                

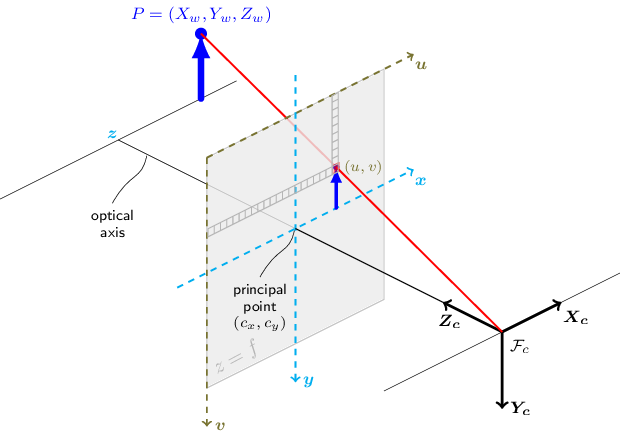
如果知道 3d点 投影到像平面的 2d点，在相机坐标系中的坐标 $U_1,\,U_2,\,U_3$，则 $\cos\theta_{23}= \dfrac {\overrightarrow{OU_2}\cdot \overrightarrow{OU_3}} {||\overrightarrow{OU_2}||\;||\overrightarrow{OU_3}||} $

具体到运算，可视为 世界坐标系 {W} 和 相机坐标系 {C} 重合，且 $Z = f$，则有

$\quad \begin{bmatrix} R & t \end{bmatrix} = \begin{bmatrix} 1 &0&0&0 \\ 0&1&0&0 \\ 0&0&1&0 \end{bmatrix} =>$ $\; s \begin{bmatrix} u \\ v \\ 1 \end{bmatrix}  =  \begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix}   \begin{bmatrix} X_c \\ Y_c \\ Z_c \end{bmatrix} $

$K^{-1}$ 可用增广矩阵求得，且 $Z_c = f$，则有

$\quad \begin{bmatrix} X_c \\Y_c\\f \end{bmatrix} = s K^{-1}\begin{bmatrix} u\\v\\1 \end{bmatrix}$

记 $\vec u = \begin{bmatrix} X_c \\ Y_c \\ Z_c \end{bmatrix}$，则 $\cos\theta_{12}=\dfrac{(K^{-1}\vec{u_1})^T (K^{-1}\vec{u_2})}{||K^{-1}\vec{u_1}||\,||K^{-1}\vec{u_2}||}$，以此类推 $\cos\theta_{23}$ 和 $\cos\theta_{31}$

3  OpenCV 函数

OpenCV 中解 PnP 的方法有 9 种，目前实现了 7 种，还有 2 种未实现，对应论文如下：

-  SOLVEPNP_P3P               Complete Solution Classification for the Perspective-Three-Point Problem

-  SOLVEPNP_AP3P             An Efficient Algebraic Solution to the Perspective-Three-Point Problem

-  SOLVEPNP_ITERATIVE             基于 L-M 最优化方法，求解重投影误差最小的位姿

-  SOLVEPNP_EPNP                           EPnP: An Accurate O(n) Solution to the PnP Problem

-  SOLVEPNP_SQPNP                         A Consistently Fast and Globally Optimal Solution to the Perspective-n-Point Problem

-  SOLVEPNP_IPPE                                        Infinitesimal Plane-based Pose Estimation    输入的 3D 点需要共面且 n ≥ 4

-  SOLVEPNP_IPPE_SQUARE                         SOLVEPNP_IPPE 的一种特殊情况，要求输入 4 个共面点的坐标，并且按照特定的顺序排列

-  SOLVEPNP_DLS (未实现)                   A Direct Least-Squares (DLS) Method for PnP     实际调用 SOLVEPNP_EPNP

-  SOLVEPNP_UPLP (未实现)                 Exhaustive Linearization for Robust Camera Pose and Focal Length Estimation    实际调用 SOLVEPNP_EPNP

3.1  solveP3P()

solveP3P() 的输入是 3 组 3d-2d 对应点，定义如下：

    // P3P has up to 4 solutions, and the solutions are sorted by reprojection errors(lowest to highest).
    int solveP3P (
        InputArray     objectPoints,     // object points, 3x3 1-channel or 1x3/3x1 3-channel. vector<Point3f> can be also passed
        InputArray      imagePoints,     // corresponding image points, 3x2 1-channel or 1x3/3x1 2-channel. vector<Point2f> can be also passed
        InputArray     cameraMatrix,     // camera intrinsic matrix
        InputArray       distCoeffs,     // distortion coefficients.If NULL/empty, the zero distortion coefficients are assumed.
        OutputArrayOfArrays   rvecs,     // rotation vectors
        OutputArrayOfArrays   tvecs,     // translation vectors
        int                   flags      // solving method
    ); 　　

3.2  solvePnP() 和 solvePnPGeneric()

solvePnP() 实际上调用的是 solvePnPGeneric()，内部实现如下：

bool solvePnP(InputArray opoints, InputArray ipoints, InputArray cameraMatrix, InputArray distCoeffs, OutputArray rvec, OutputArray tvec, bool useExtrinsicGuess, int flags)
{
    CV_INSTRUMENT_REGION();

    vector<Mat> rvecs, tvecs;
    int solutions = solvePnPGeneric(opoints, ipoints, cameraMatrix, distCoeffs, rvecs, tvecs, useExtrinsicGuess, (SolvePnPMethod)flags, rvec, tvec);

    if (solutions > 0)
    {
        int rdepth = rvec.empty() ? CV_64F : rvec.depth();
        int tdepth = tvec.empty() ? CV_64F : tvec.depth();
        rvecs[0].convertTo(rvec, rdepth);
        tvecs[0].convertTo(tvec, tdepth);
    }

    return solutions > 0;
}　　

solvePnPGeneric() 除了求解相机位姿外，还可得到重投影误差，其定义如下：

    bool solvePnPGeneric (
        InputArray         objectPoints,    // object points, Nx3 1-channel or 1xN/Nx1 3-channel, N is the number of points. vector<Point3d> can be also passed
        InputArray          imagePoints,    // corresponding image points, Nx2 1-channel or 1xN/Nx1 2-channel, N is the number of points. vector<Point2d> can be also passed
        InputArray         cameraMatrix,    // camera intrinsic matrix
        InputArray           distCoeffs,    // distortion coefficients
        OutputArrayOfArrays        rvec,    // rotation vector
        OutputArrayOfArrays        tvec,    // translation vector
        bool  useExtrinsicGuess = false,    // used for SOLVEPNP_ITERATIVE. If true, use the provided rvec and tvec as initial approximations, and further optimize them.
        SolvePnPMethod  flags = SOLVEPNP_ITERATIVE, // solving method
        InputArray               rvec = noArray(),  // initial rotation vector when using SOLVEPNP_ITERATIVE and useExtrinsicGuess is set to true
        InputArray               tvec = noArray(),  // initial translation vector when using SOLVEPNP_ITERATIVE and useExtrinsicGuess is set to true
        OutputArray reprojectionError = noArray()   // optional vector of reprojection error, that is the RMS error
    ); 　　

3.3  solvePnPRansac()

solvePnP() 的一个缺点是鲁棒性不强，对异常点敏感，这在相机标定中问题不大，因为标定板的图案已知，并且特征提取较为稳定

然而，当相机拍摄实际物体时，因为特征难以稳定提取，会出现一些异常点，导致位姿估计的不准，因此，需要一种处理异常点的方法

RANSAC 便是一种高效剔除异常点的方法，对应 solvePnPRansac()，它是一个重载函数，共有 2 种参数形式，第 1 种形式如下：

    bool solvePnPRansac (
        InputArray         objectPoints,    // object points, Nx3 1-channel or 1xN/Nx1 3-channel, N is the number of points. vector<Point3d> can be also passed
        InputArray          imagePoints,    // corresponding image points, Nx2 1-channel or 1xN/Nx1 2-channel, N is the number of points. vector<Point2d> can be also passed
        InputArray         cameraMatrix,    // camera intrinsic matrix
        InputArray           distCoeffs,    // distortion coefficients
        OutputArray                rvec,    // rotation vector
        OutputArray                tvec,    // translation vector
        bool  useExtrinsicGuess = false,    // used for SOLVEPNP_ITERATIVE. If true, use the provided rvec and tvec as initial approximations, and further optimize them.
        int       iterationsCount = 100,    // number of iterations
        float   reprojectionError = 8.0,    // inlier threshold value. It is the maximum allowed distance between the observed and computed point projections to consider it an inlier
        double        confidence = 0.99,    // the probability that the algorithm produces a useful result
        OutputArray inliers = noArray(),    // output vector that contains indices of inliers in objectPoints and imagePoints
        int  flags = SOLVEPNP_ITERATIVE     // solving method
    );　　

3.4  solvePnPRefineLM() 和 solvePnPRefineVVS()

OpenCV 中还有 2 个位姿细化函数：通过迭代不断减小重投影误差，从而求得最佳位姿，solvePnPRefineLM() 使用 L-M 算法，solvePnPRefineVVS() 则用虚拟视觉伺服 (Virtual Visual Servoing)

solvePnPRefineLM() 的定义如下：

  void solvePnPRefineLM (
      InputArray      objectPoints,  // object points, Nx3 1-channel or 1xN/Nx1 3-channel, N is the number of points
      InputArray       imagePoints,  // corresponding image points, Nx2 1-channel or 1xN/Nx1 2-channel
      InputArray      cameraMatrix,  // camera intrinsic matrix
      InputArray        distCoeffs,  // distortion coefficients
      InputOutputArray      rvec,      // input/output rotation vector
      InputOutputArray      tvec,      // input/output translation vector
      TermCriteria  criteria = TermCriteria(TermCriteria::EPS+TermCriteria::COUNT, 20, FLT_EPSILON) // Criteria when to stop the LM iterative algorithm
); 　　

4  应用实例

4.1  位姿估计 (静态+标定板)

当手持标定板旋转不同角度时，利用相机内参 + solvePnP()，便可求出相机相对标定板的位姿

#include "opencv2/imgproc.hpp"
#include "opencv2/highgui.hpp"
#include "opencv2/calib3d.hpp"

using namespace std;
using namespace cv;

Size kPatternSize = Size(9, 6);
float kSquareSize = 0.025;
// camera intrinsic parameters and distortion coefficient
const Mat cameraMatrix = (Mat_<double>(3, 3) << 5.3591573396163199e+02, 0.0, 3.4228315473308373e+02,
                                                0.0, 5.3591573396163199e+02, 2.3557082909788173e+02,
                                                0.0, 0.0, 1.0);
const Mat distCoeffs = (Mat_<double>(5, 1) << -2.6637260909660682e-01, -3.8588898922304653e-02, 1.7831947042852964e-03,
                                              -2.8122100441115472e-04, 2.3839153080878486e-01);

int main()
{
    // 1) read image
    Mat src = imread("left07.jpg");
    if (src.empty())
        return -1;
    // prepare for subpixel corner
    Mat src_gray;
    cvtColor(src, src_gray, COLOR_BGR2GRAY);

    // 2) find chessboard corners and subpixel refining
    vector<Point2f> corners;
    bool patternfound = findChessboardCorners(src, kPatternSize, corners);
    if (patternfound) {
        cornerSubPix(src_gray, corners, Size(11, 11), Size(-1, -1), TermCriteria(TermCriteria::EPS + TermCriteria::MAX_ITER, 30, 0.1));
    }
    else {
        return -1;
    }

    // 3) object coordinates
    vector<Point3f> objectPoints;
    for (int i = 0; i < kPatternSize.height; i++)
    {
        for (int j = 0; j < kPatternSize.width; j++)
        {
            objectPoints.push_back(Point3f(float(j * kSquareSize), float(i * kSquareSize), 0));
        }
    }

    // 4) Rotation and Translation vectors
    Mat rvec, tvec;
    solvePnP(objectPoints, corners, cameraMatrix, distCoeffs, rvec, tvec);

    // 5) project estimated pose on the image
    drawFrameAxes(src, cameraMatrix, distCoeffs, rvec, tvec, 2*kSquareSize);
    imshow("Pose estimation", src);
    waitKey();
}　　

当标定板旋转不同角度时，相机所对应的各个位姿如下：

            

4.2  位姿估计 (实时+任意物)

OpenCV 中有一个实时目标跟踪例程，位于 "opencv\samples\cpp\tutorial_code\calib3d\real_time_pose_estimation" 中，实现步骤如下：

1)  读取目标的三维模型和网格 -> 2)  获取视频流 -> 3)  ORB 特征检测 -> 4) 3d-2d 特征匹配 -> 5)  相机位姿估计 -> 6)  卡尔曼滤波

例程中设计了一个 PnPProblem 类来实现位姿估计，其中 2 个重要的函数 estimatePoseRANSAC() 和 backproject3DPoint() 定义如下：

    class PnPProblem
    {
    public:
        explicit PnPProblem(const double param[]);  // custom constructor
        virtual ~PnPProblem();

        cv::Point2f backproject3DPoint(const cv::Point3f& point3d);

        void estimatePoseRANSAC(const std::vector<cv::Point3f>& list_points3d, const std::vector<cv::Point2f>& list_points2d,
                                int flags, cv::Mat& inliers, int iterationsCount, float reprojectionError, double confidence);
        // ...
    }

    // Custom constructor given the intrinsic camera parameters
    PnPProblem::PnPProblem(const double params[])
    {
        // intrinsic camera parameters
        _A_matrix = cv::Mat::zeros(3, 3, CV_64FC1);
        _A_matrix.at<double>(0, 0) = params[0];       //  [ fx   0  cx ]
        _A_matrix.at<double>(1, 1) = params[1];       //  [  0  fy  cy ]
        _A_matrix.at<double>(0, 2) = params[2];       //  [  0   0   1 ]
        _A_matrix.at<double>(1, 2) = params[3];
        _A_matrix.at<double>(2, 2) = 1;
        // rotation matrix, translation matrix, rotation-translation matrix
        _R_matrix = cv::Mat::zeros(3, 3, CV_64FC1);
        _t_matrix = cv::Mat::zeros(3, 1, CV_64FC1);
        _P_matrix = cv::Mat::zeros(3, 4, CV_64FC1);
    }

    // Estimate the pose given a list of 2D/3D correspondences with RANSAC and the method to use
    void PnPProblem::estimatePoseRANSAC (
        const std::vector<Point3f>& list_points3d,        // list with model 3D coordinates
        const std::vector<Point2f>& list_points2d,        // list with scene 2D coordinates
        int flags, Mat& inliers, int iterationsCount,     // PnP method; inliers container
        float reprojectionError, float confidence)        // RANSAC parameters
    {
        // distortion coefficients, rotation vector and translation vector
        Mat distCoeffs = Mat::zeros(4, 1, CV_64FC1);
        Mat rvec = Mat::zeros(3, 1, CV_64FC1);
        Mat tvec = Mat::zeros(3, 1, CV_64FC1);
        // no initial approximations
        bool useExtrinsicGuess = false;           

        // PnP + RANSAC
        solvePnPRansac(list_points3d, list_points2d, _A_matrix, distCoeffs, rvec, tvec, useExtrinsicGuess, iterationsCount, reprojectionError, confidence, inliers, flags);

        // converts Rotation Vector to Matrix
        Rodrigues(rvec, _R_matrix);
        _t_matrix = tvec;                            // set translation matrix
        this->set_P_matrix(_R_matrix, _t_matrix);    // set rotation-translation matrix
    }

    // Backproject a 3D point to 2D using the estimated pose parameters
    cv::Point2f PnPProblem::backproject3DPoint(const cv::Point3f& point3d)
    {
        // 3D point vector [x y z 1]'
        cv::Mat point3d_vec = cv::Mat(4, 1, CV_64FC1);
        point3d_vec.at<double>(0) = point3d.x;
        point3d_vec.at<double>(1) = point3d.y;
        point3d_vec.at<double>(2) = point3d.z;
        point3d_vec.at<double>(3) = 1;

        // 2D point vector [u v 1]'
        cv::Mat point2d_vec = cv::Mat(4, 1, CV_64FC1);
        point2d_vec = _A_matrix * _P_matrix * point3d_vec;

        // Normalization of [u v]'
        cv::Point2f point2d;
        point2d.x = (float)(point2d_vec.at<double>(0) / point2d_vec.at<double>(2));
        point2d.y = (float)(point2d_vec.at<double>(1) / point2d_vec.at<double>(2));

        return point2d;
    }

PnPProblem 类的调用如下：实例化 -> estimatePoseRansac() 估计位姿 -> backproject3DPoint() 画出位姿

// Intrinsic camera parameters: UVC WEBCAM
double f = 55;                     // focal length in mm
double sx = 22.3, sy = 14.9;       // sensor size
double width = 640, height = 480;  // image size
double params_WEBCAM[] = { width * f / sx,   // fx
                           height * f / sy,  // fy
                           width / 2,      // cx
                           height / 2 };   // cy
// instantiate PnPProblem class
PnPProblem pnp_detection(params_WEBCAM);

// RANSAC parameters
int iterCount = 500;        // number of Ransac iterations.
float reprojectionError = 2.0;    // maximum allowed distance to consider it an inlier.
float confidence = 0.95;          // RANSAC successful confidence.

// OpenCV requires solvePnPRANSAC to minimally have 4 set of points
if (good_matches.size() >= 4)
{
    // -- Step 3: Estimate the pose using RANSAC approach
    pnp_detection.estimatePoseRANSAC(list_points3d_model_match, list_points2d_scene_match,
        pnpMethod, inliers_idx, iterCount, reprojectionError, confidence);

    // ... ..
}

// ... ...　

float fp = 5;
vector<Point2f> pose2d;
pose2d.push_back(pnp_detect_est.backproject3DPoint(Point3f(0, 0, 0))); // axis center
pose2d.push_back(pnp_detect_est.backproject3DPoint(Point3f(fp, 0, 0))); // axis x
pose2d.push_back(pnp_detect_est.backproject3DPoint(Point3f(0, fp, 0))); // axis y
pose2d.push_back(pnp_detect_est.backproject3DPoint(Point3f(0, 0, fp))); // axis z

draw3DCoordinateAxes(frame_vis, pose2d); // draw axes

// ... ...

　　实时目标跟踪的效果如下：

   　　

　

参考资料

OpenCV-Python Tutorials / Camera Calibration and 3D Reconstruction / Pose Estimation

OpenCV Tutorials / Camera calibration and 3D reconstruction (calib3d module) / Real time pose estimation of a textured object

一种改进的 PnP 问题求解算法研究[J]

Perspective-n-Point, Hyun Soo Park