[CSP-S2021] 回文

链接：

P7915

---

题意：

给出一个长度为 \(2n\) 的序列 \(a\)，其中 \(1\sim n\) 每个数出现了 2 次。有 L,R 两种操作分别是将 \(a\) 的开头或末尾元素加入到初始为空的序列 \(b\) 里，目标是让 \(b\) 成为一个回文串。

需要判断无解或求出字典序最小的方案。

\(T(T\leq100)\) 组数据，对于每组数据 \(n\leq5\times10^5\)。\(\sum n\leq5\times10^5\)。

---

分析：

首先对于 \(a\) 串，一定存在一个分界点使得左边的元素是通过 L 操作弹出的，右边的元素是通过 R 操作弹出的，显然 \(b\) 的末尾就在这个分界点的两边，显然 \(b\) 的末尾一定是 \(a\) 的开头或结尾，这里先假设是开头。

那么找到这个分界点，也就是与 \(a_1\) 相同的位置。发现序列被分成了两段，左边一段是从左往右通过 L 操作弹出的，右边一段是从右往左通过 R 操作弹出的，那么我们把这两段拉出来，这里有个细节就是分界点要分在左边一段，因为要求字典序最小。

假设与 \(a_1\) 相等的地方是 \(i\)，\(i\) 的下一个位置是 \(j\)，大概就是：

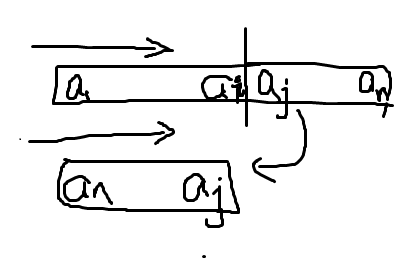
变成了两个队列，队首在 \(b\) 的前面，队尾在 \(b\) 的后面，那么只要队首和队尾能配对，就贪心选择字典序小的并加入到 \(b\) 里就可以了。

然后如果 \(b\) 的末尾是 \(a\) 的末尾，就重新找分界点再做一遍就行了。

另外，可能会存在 \(a\) 的开头等于 \(a\) 的末尾的情况，此时除非原始串就是回文串，否则是无解的，特判一下就行了。

---

算法：

找到分界点，维护两个双端队列，贪心选择即可。

---

代码：

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define in read()
inline int read(){
	int p=0,f=1;
	char c=getchar();
	while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
	while(isdigit(c)){p=p*10+c-'0';c=getchar();}
	return p*f;
}
const int N=5e5+5;
int T,n,a[N<<1];
int flag,s,e;
int A[N<<1],ai,an;
int B[N<<1],bi,bn;
int ans[N<<1];
signed main(){
	freopen("palin.in","r",stdin);
	freopen("palin.out","w",stdout);
	T=in;
	while(T--){
		flag=1;n=in;
		for(int i=1;i<=(n<<1);i++)a[i]=in;
		for(int i=1;i<=n;i++)
			if(a[i]!=a[(n<<1)-i+1])flag=0;
		for(int i=2;i<(n<<1);i++){
			if(a[i]==a[1])s=i;
			if(a[i]==a[(n<<1)])e=i;
		}
		if(a[1]==a[(n<<1)]){
			if(flag){for(int i=1;i<=(n<<1);i++)putchar('L');puts("");}
			else puts("-1");
			continue;
		}
		for(int i=1;i<=s;i++)A[i]=a[i];an=s;bn=(n<<1)-s;
		for(int i=(n<<1);i>=s+1;i--)B[(n<<1)-i+1]=a[i];
		ai=1,bi=1,flag=0;
		for(int i=1;i<=n;i++){
			if(ai<an&&A[ai]==A[an])
				ans[i]=ans[(n<<1)-i+1]='L',ai++,an--;
			else if(ai<=an&&bi<=bn&&A[ai]==B[bn])
				ans[i]='L',ans[(n<<1)-i+1]='R',ai++,bn--;
			else if(bi<bn&&B[bi]==B[bn])
				ans[i]=ans[(n<<1)-i+1]='R',bi++,bn--;
			else if(ai<=an&&bi<=bn&&B[bi]==A[an])
				ans[i]='R',ans[(n<<1)-i+1]='L',bi++,an--;
			else flag=1;
		}
		if(!flag){
			for(int i=1;i<=(n<<1);i++)
				cout<<(char)ans[i];
			puts("");
		}
		else{
			s=e;
			for(int i=1;i<=s;i++)A[i]=a[i];an=s;bn=(n<<1)-s;
			for(int i=(n<<1);i>=s+1;i--)B[(n<<1)-i+1]=a[i];
			ai=1,bi=1,flag=0;
			for(int i=1;i<=n;i++){
				if(ai<an&&A[ai]==A[an])
					ans[i]=ans[(n<<1)-i+1]='L',ai++,an--;
				else if(ai<=an&&bi<=bn&&A[ai]==B[bn])
					ans[i]='L',ans[(n<<1)-i+1]='R',ai++,bn--;
				else if(bi<bn&&B[bi]==B[bn])
					ans[i]=ans[(n<<1)-i+1]='R',bi++,bn--;
				else if(ai<=an&&bi<=bn&&B[bi]==A[an])
					ans[i]='R',ans[(n<<1)-i+1]='L',bi++,an--;
				else flag=1;
			}
			if(!flag){
				for(int i=1;i<=(n<<1);i++)
					cout<<(char)ans[i];
				puts("");
			}
			else puts("-1");
		}
	}
	return 0;
}

---

题外话：

没想到会这么简单，失策了