2020ICPC上海站 C. Sum of Log

题目大意：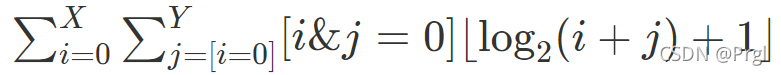

给定T组X,Y，对于每组X,Y，求上面式子   的值，其中  当x为真时等于1，其他情况等于0. 其中。

思路：

对X,Y一起进行数位DP，我们把每一位枚举数字的上限以及数字之前是否有前导零（当X,Y枚举到这一位二者都有前导零时才为true）都直接记录到这一位的状态里面，然后在枚举每一位的时候，枚举X，Y在这一位上面所有可能的组合（i，j)。如果i&j为1，那么X&Y就一定不为0，便不会对答案产生贡献，这种情况下的后面若干位就不用枚举了。否则，对答案产生了贡献，由于在X&Y=0的时候二者相加不会进位，所以对答案的贡献就是二者中最高位的1的pos + 1。以此阶段之后枚举的所有合法数字都会产生同样的这一个贡献，所以ans+=dfs()*(pos+1)（之后的数字lead都不会为true，所以这里的dfs返回的实际是合法数字的个数），否则ans+=dfs()（仅统计合法数字的个数，避免重复的计算）。

最后答案为dfs(pos-1,true,true,true)-1（因为0，0不考虑，所以要减去）

由于每次构成dp状态的数字的组成都不一样，所以必须在循环内memset

代码：

#include<bits/stdc++.h>
#include<unordered_map>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> PII;
//#define int LL
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#pragma warning(disable :4996)
const int maxn = 100010;
const double eps = 1e-6;
const int mod = 1000000007;
const LL MOD = 998244353;

int T;
int X, Y;
int x[35], y[35];
LL dp[35][2][2][2];//位，x上限，y上限，前导零
//lead:x,y当前同时有前导零
LL dfs(int pos, bool xlim, bool ylim, bool lead)//把限制直接搞成状态
{
	if (pos == -1)
		return 1;
	if (dp[pos][xlim][ylim][lead] != -1)
		return dp[pos][xlim][ylim][lead];
	int upx = (xlim ? x[pos] : 1);
	int upy = (ylim ? y[pos] : 1);
	LL ans = 0;
	for (int i = 0; i <= upx; i++)
	{
		for (int j = 0; j <= upy; j++)
		{
			if (i & j)
				continue;//数字非法，不往下进行枚举
			int cnt = 1;
			if (lead && (i || j))
				cnt = pos + 1;
			ans = (ans + dfs(pos - 1, xlim && i == upx, ylim && j == upy, lead && !i && !j) * cnt % mod) % mod;
		}
	}

	return dp[pos][xlim][ylim][lead] = ans;
}

int calc(int a, int b)
{
	memset(x, 0, sizeof(x));
	memset(y, 0, sizeof(y));
	int pos1 = 0, pos2 = 0;
	while (a)
	{
		x[pos1++] = a % 2;
		a >>= 1;
	}
	while (b)
	{
		y[pos2++] = b % 2;
		b >>= 1;
	}
	return dfs(max(pos1, pos2) - 1, true, true, true);
}

void solve()
{
	cout << (calc(X, Y) - 1 + mod) % mod << endl;
}

int main()
{
	cin >> T;
	while (T--)
	{
		memset(dp, -1, sizeof(dp));
		cin >> X >> Y;
		solve();
	}

	return 0;
}