间断有限元h自适应处理方法

细分单元

function Hrefine2D(refineflag)

根据refineflag变量细分单元，其中refineflag变量大小为 [Kx1]，需要细分单元标记为1，不需要单元为0。

根据refineflag修改EToV，VX、VY，BCType三组变量。（EToE及EToF会在Setup2D.m脚本中，根据EToV得到）

整个函数分三步：

1. 判断需增加多少个新顶点
2. 计算新顶点位置
3. 修改EToV，VX、VY，BCType三组变量，将新得到的细分单元添加到对应位置

1.统计细分顶点个数

根据Hesthaven(2007)的Nodal discontinuous Galerkin methods - algorithms, analysis, and applications第9章，细分单元采用Four-way element refinement方法——即每个单元等分为四个三角形单元。

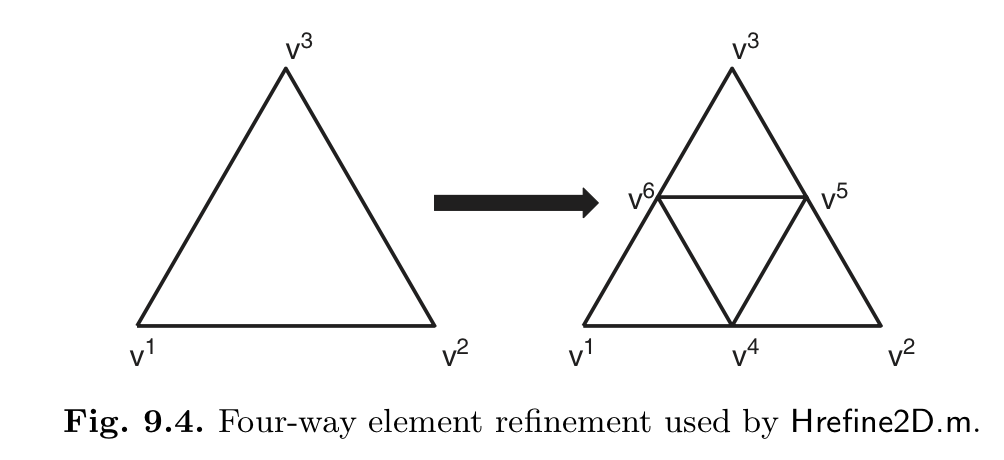
每个细分单元新增加三个顶点，分别为 \(v^4,v^5,v^6\)。但是周围也有单元进行细分时情形就比较复杂，主要分为两种情况：

1. 只有 \(K_1\) 进行细分
2. \(K_1,K_2\) 同时进行细分

当只对相邻单元中的一个进行细分时，如下图所示，新增加的三个顶点继续进行编号。（注意，因为顶点是唯一的，因此两单元公共顶点编号相同）

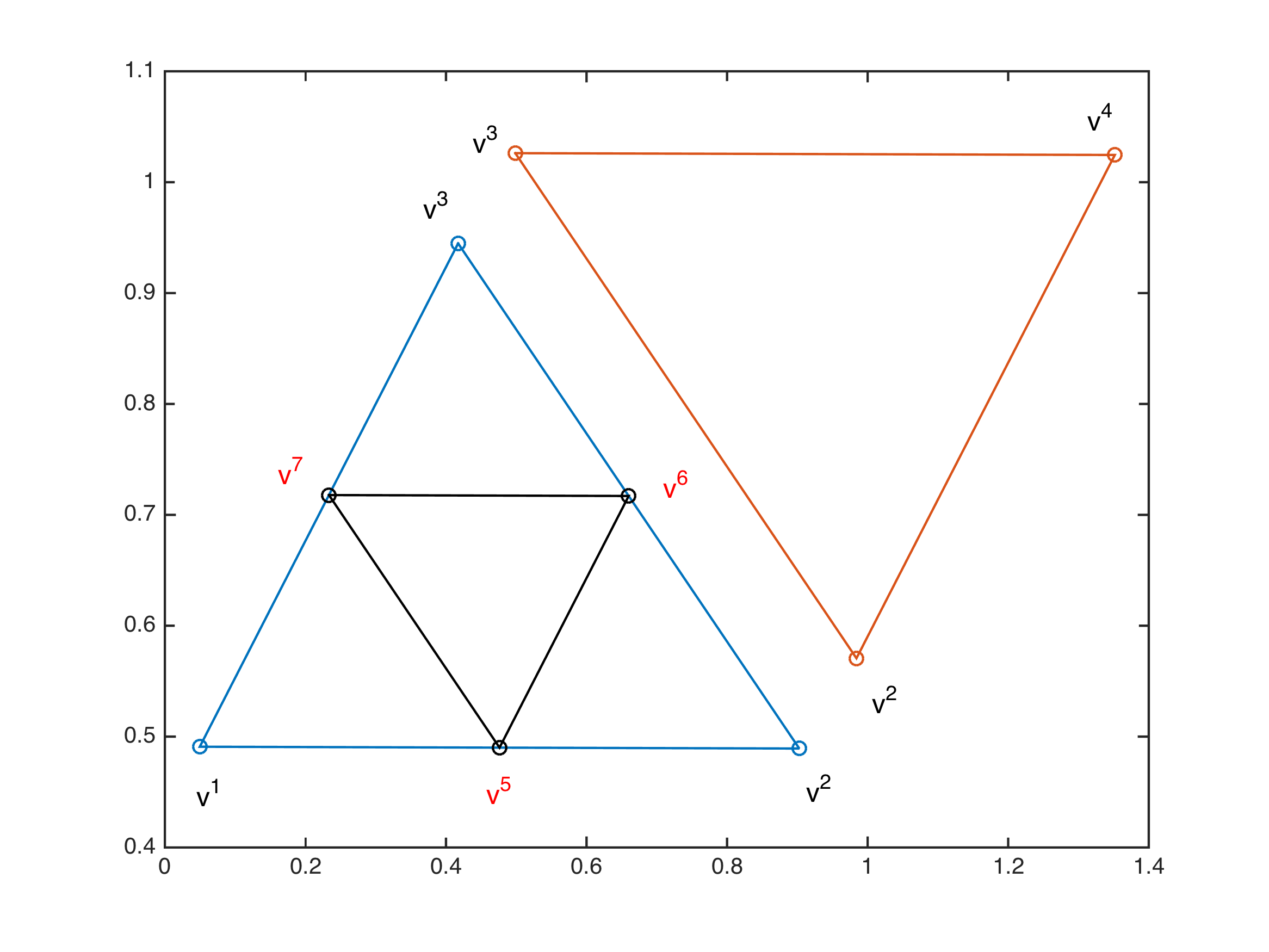
当相邻单元都进行细分时，如下图，此时两个单元新划分的顶点 \(v^6\) 也是一个公共顶点，因此编号相同。即新增加的是五个顶点（\(v^5\) ~ \(v^9\)），而非两个单元各三个顶点。

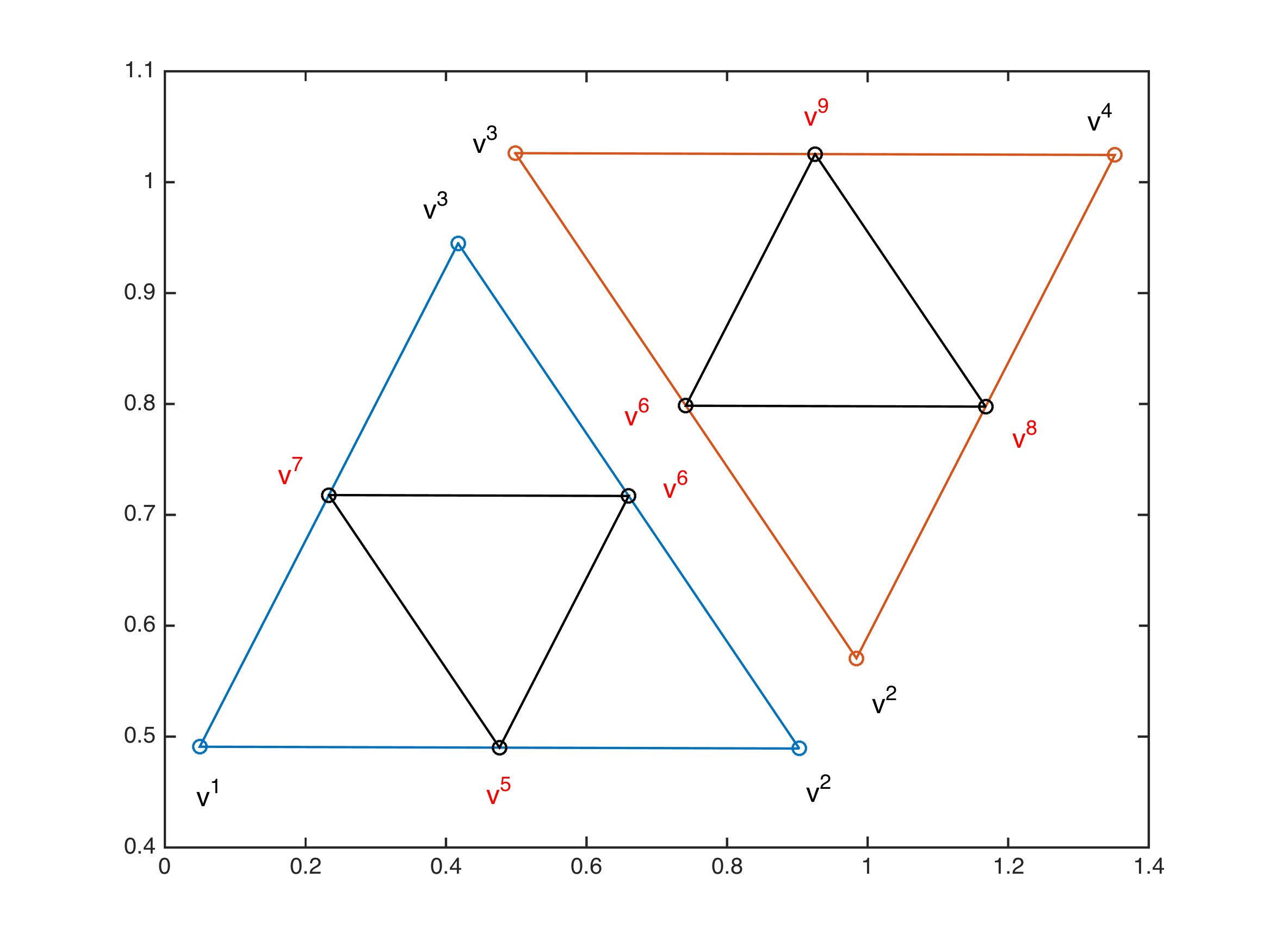
所以，细分单元时我们需统计不同边的个数，具体方法如下

统计需要细分单元个数Nrefine，及对应单元序号ref

% 1.1 Count vertices
Nv = length(VX(:));

% 1.2 Find and count elements to be refined
ref = sort(find(refineflag));
Nrefine = length(ref);

找到细分单元三个顶点的序列v1、v2、v3等，随后统计需要增加节点个数ids

% 1.3 Extract vertex numbers of elements to refine
v1 = EToV(ref, 1); v2 = EToV(ref, 2); v3 = EToV(ref, 3);

首先获取每个需要细分单元三个面及其对应面的序号，例如，单元k1中面f1，对应的面是k2单元中f2，随后取这两个面序号的最大值作为此细分单元面上顶点的标记。这样，假如两个面是相邻的，而且所在两个单元都需要细分，那么这两个面新增加顶点的标记相同，即只增加一个顶点。

% 1.4 Uniquely number all face centers
v4 = max( 1 + Nfaces*(0:K-1)', EToF(:,1) + Nfaces*(EToE(:,1)-1) );
v5 = max( 2 + Nfaces*(0:K-1)', EToF(:,2) + Nfaces*(EToE(:,2)-1) );
v6 = max( 3 + Nfaces*(0:K-1)', EToF(:,3) + Nfaces*(EToE(:,3)-1) );

获得细分单元三个面上对应标记

% 2.0 Extract face center vertices for elements to refine
v4 = v4(ref);      v5 = v5(ref);      v6 = v6(ref);

去掉这些标记中重复部分，获得不重复的标记序列ids

% 2.1 Renumber face centers contiguously from Nv+1
ids = unique([v4;v5;v6]);

length(ids)即为增加节点个数，newids变量是使在ids储存的序号位置上分别赋值为1、2、3……

newids(ids) = (1:length(ids))';

最终，确定新顶点序号v4、v5、v6。

v4 = Nv+newids(v4)'; v5 = Nv+newids(v5)'; v6 = Nv+newids(v6)';

由此可看出，新顶点顺序是根据面序号确定的：

1. 假如相邻两个单元只有一个需要细分，那么细分单元的面序号为新顶点标记
2. 假如相邻两个单元都需要细分，那么取本单元面序号与相邻单元面序号中较大的作为新顶点标记

最终，根据顶点标记大小确定新顶点的序号。

2.更新EToV变量

% 2.2 Replace original triangle with triangle connecting edge centers
EToV(ref,:) = [v4,v5,v6];

中间小三角形使用原始单元序号，对应三个顶点为[v4, v5, v6]。其他三个三角形作为新增单元进行编号，顶点顺序分别为[v1, v4, v6]，[v2, v5, v4]，[v3, v6, v5]。

% 3.0 Add extra triangles to EToV
EToV(K+1:K+3*Nrefine,1) = [v1;v2;v3]; % first  vertices of new elements
EToV(K+1:K+3*Nrefine,2) = [v4;v5;v6]; % second vertices of new elements
EToV(K+1:K+3*Nrefine,3) = [v6;v4;v5]; % third  vertices of new elements

3.更新BCType变量

4.更新顶点序列VX，VY及单元数K

顶点个数增加length(ids)个，新的顶点坐标如下

% 3.2 Find vertex locations of elements to be refined
x1 = VX(v1);  x2 = VX(v2);  x3 = VX(v3);
y1 = VY(v1);  y2 = VY(v2);  y3 = VY(v3);    

% 3.3 Add coordinates for refined edge centers
VX(v4) = 0.5*(x1+x2); VX(v5) = 0.5*(x2+x3); VX(v6) = 0.5*(x3+x1);
VY(v4) = 0.5*(y1+y2); VY(v5) = 0.5*(y2+y3); VY(v6) = 0.5*(y3+y1);

单元个数增加3*Nrefine，即3倍的细分单元数

% 3.4 Increase element count
K = K+3*Nrefine;

统计单元拓扑关系

[EToE,EToF]= tiConnect2D(EToV)

根据EToV变量获得单元与单元EToE及单元与面EToF之间对应关系。

这里采用的方法要比函数Connect2D.m更简单些，主要是通过判断每个面两端顶点序号是否相等。

Nfaces=3;
K = size(EToV,1);
Nnodes = max(max(EToV));

首先将每个面两个顶点序号组成数组fnodes，其顺序按照变量EToV的列进行循环

% create list of all faces 1, then 2, & 3
fnodes = [EToV(:,[1,2]);EToV(:,[2,3]);EToV(:,[3,1])];

将fnodes每行进行排序，顶点序号有小到大，并且序号值减一

fnodes = sort(fnodes,2)-1;

初始化EToE与EToV，此时默认单元与自己相邻

% set up default element to element and Element to faces connectivity
EToE= (1:K)'*ones(1,Nfaces); EToF= ones(K,1)*(1:Nfaces);

随后根据每个面两端节点号给出一个对应标记值，公式为

\[\begin{equation}
f = v1 \times Nnodes + v2
\end{equation}\]

其中\(v1\)为较小的顶点标号，\(v2\)为较大的顶点标号。由此可看出，若两个面顶点序号相同，那么其表极值\(f\)也相等。据此，我们就可以找到相邻的两个面序号

% uniquely number each set of three faces by their node numbers
id = fnodes(:,1)*Nnodes + fnodes(:,2)+1;

随后就是寻找具有相同标记值得两个面。定义矩阵spNodeToNode，其中第一列为标记值，第二列为面序号，第三列为该面所在单元，第四列为该面在单元内局部序号

spNodeToNode=[id, (1:Nfaces*K)', EToE(:), EToF(:)];

按照标记值进行排序，找到有对应面所在的行，即indices，其对应面所在行即为indices+1

% Now we sort by global face number.
sorted=sortrows(spNodeToNode,1);

% find matches in the sorted face list
[indices,dummy]=find( sorted(1:(end-1),1)==sorted(2:end,1) );

对EToE与EToF进行赋值

% make links reflexive
matchL = [sorted(indices,:)   ;sorted(indices+1,:)];
matchR = [sorted(indices+1,:) ;sorted(indices,:)];

% insert matches
EToE(matchL(:,2)) = matchR(:,3); EToF(matchL(:,2)) = matchR(:,4);

总结：可以看到，函数tiConnect2D仅利用相邻面具有相同节点序号这一性质，找到了计算EToE与EToF简单算法。

non-conforming网格中通量计算

对于在这种细分之后网格上计算，关键问题是边界通量处理。

例如Maxwell方程中，三个方程为

\[\begin{eqnarray}
\begin{aligned}
& \left\{\begin{array}{l}
\frac{\partial H_x}{\partial t} = -\frac{\partial E}{\partial y} \cr
\frac{\partial H_y}{\partial t} = \frac{\partial E}{\partial x} \cr
\frac{\partial E}{\partial t} = \frac{\partial H_y}{\partial x} - \frac{\partial H_x}{\partial y}
\end{array} \right.
\end{aligned}
\end{eqnarray}\]

以第一个方程离散为例，得到

\[\begin{eqnarray}
\begin{aligned}
& \left\{\begin{array}{l}
\frac{dH_x}{dt} = -D_y E + \frac{1}{2} \left(JM \right)^{-1} \int_{\partial D} \left(n_y \left[E \right] + \alpha \left[n_x H_n \right] - \left[ H_x \right] \right)l(x) \mathrm{ds}
\end{array} \right. \cr
\end{aligned}
\end{eqnarray}\]

其中右端边界通量积分，简写为

\[\int_{\partial D} l(x) \cdot F_n^{*} \mathrm{ds}
\]

其中

\[l = [l_0(x), l_1(x), \cdots l_{p-1}(x)]^T
\]

而

\[F_n^* = \vec{n}\cdot F^* = [l_{g_0}(x), l_{g_1}(x), \cdots l_{g_{n-1}}(x)] \cdot
\begin{bmatrix}
F_n^*(x_{g_0}) \cr
F_n^*(x_{g_1}) \cr
\cdots \cr
F_n^*(x_{g_{n-1}})
\end{bmatrix}\]

p为单元内基函数个数，而n为边上Gauss积分节点个数，\(g_{n-1}\)为积分节点序号。

由此，可看出计算通量主要分两个步骤

1. 获得边界Gauss点处通量值\(F_n^*(x_{g_0})\)
2. 构造积分质量矩阵IM

这两个步骤主要在函数BuildHNonCon2D中，定义为

[neighbors] = BuildHNonCon2D(NGauss, tol)

获得长度为2的直线上Gauss节点分布

% 1. Build Gauss nodes
[gz, gw] = JacobiGQ(0, 0, NGauss-1);

寻找细分后non-conforming的边界面

non-conforming主要指如下图情况

左面单元细分后，产生4个新单元，但是右侧单元边界无法与左侧细分得到的新单元边界完全对应。因此，左侧细分单元面 \(v^3-v^6\)，\(v^6-v^2\) 与右侧单元 \(v^3-v^2\) 即为三个需特殊处理的non-conforming面。

注意，在单元细分后更新单元间拓扑关系时，若两单元边界面节点不同，那么在边界处没有单元与之对应，EToE将储存自身单元序号。

% 1.1 Find location of vertices of boundary faces
vx1 = VX(EToV(:,[1,2,3])); vx2 = VX(EToV(:,[2,3,1]));
vy1 = VY(EToV(:,[1,2,3])); vy2 = VY(EToV(:,[2,3,1]));

寻找没有相邻单元的面序号idB

idB = find(EToE==((1:K)'*ones(1,Nfaces)));

获得这些面的顶点坐标x1，y1与x2，y2

x1 = vx1(idB)'; y1 = vy1(idB)';
x2 = vx2(idB)'; y2 = vy2(idB)';

获得这些面的单元序号elemtsB与局部单元序号facesB

% 1.2 Find those element-faces that are on boundary faces
[elmtsB,facesB] = find(EToE==((1:K)'*ones(1,Nfaces)));
Nbc = length(elmtsB); % No. of boundary faces

下面则开始对这些边界面循环，找出与其对应的面，并计算插值矩阵与积分质量矩阵。

寻找对应面

首先获得本边界面的单元编号、局部面编号与顶点坐标 \([x11, y11]\)，\([x12, y12]\)

% 2.2 Find element and face of this boundary face
  k1 = elmtsB(b1); f1 = facesB(b1);

  % 2.3 Find end coordinates of b1'th boundary face
  x11 = x1(b1);  y11 = y1(b1);  x12 = x2(b1);  y12 = y2(b1);

non-conforming对应面分三种情况：

1. 面1包含面2
2. 面2与面2交错
3. 面1被包含于面2
   
   三种情形示意图如下图所示

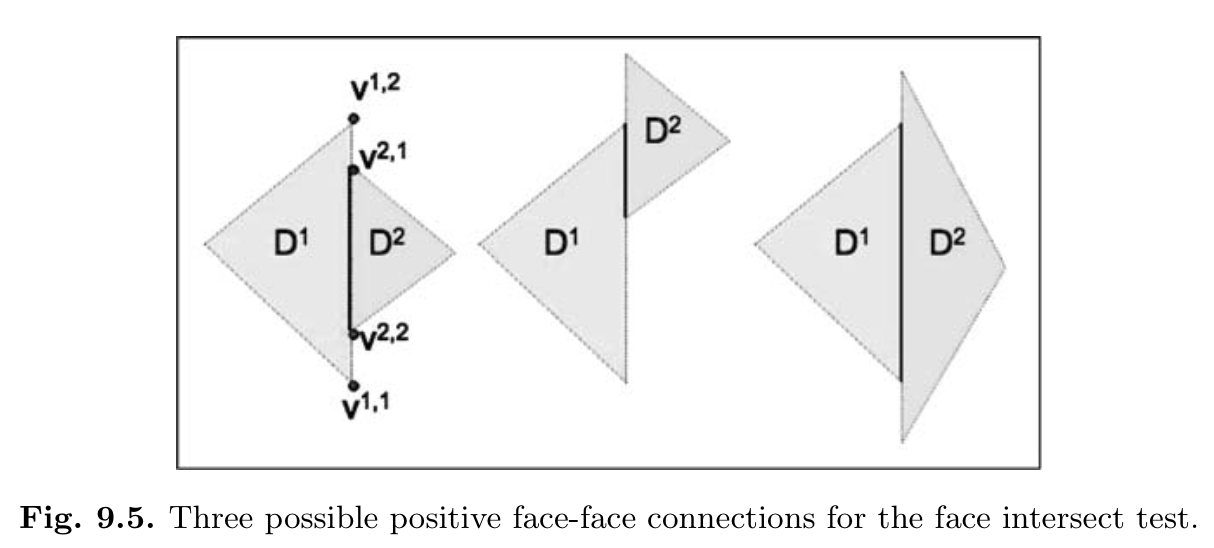
只有两个面有以上三种情形之一时，才认为两个面是对应的。

以上三种情况必须具有以下三个条件：

1.两个面的四个顶点是共线的

共线判定可以根据面1顶点与面2的一个顶点组成平行四边形来判断，若平行四边形面积为0，则面2的顶点就位于面1直线上

area1 = abs((x12-x11)*(y1-y11) - (y12-y11)*(x1-x11)); %scale
area2 = abs((x12-x11)*(y2-y11) - (y12-y11)*(x2-x11));

2.两个面有公共部分

面1顶点\(v^{1,1}\)，\(v^{1,2}\)在面2直线上法向投影点\(v_n^{1,1}\)，\(v_n^{1,2}\)，将投影点利用面2顶点线性组合得到，组合参数为

\[\begin{eqnarray}
\begin{aligned}
& v_n^{1,1} = \frac{1-r^1}{2}v^{2,1} + \frac{1+r^1}{2}v^{2,2} \cr
& v_n^{1,2} = \frac{1-r^2}{2}v^{2,1} + \frac{1+r^2}{2}v^{2,2}
\end{aligned}
\end{eqnarray}\]

当\(r^1\)，\(r^2\)有如下关系时，两面不对应

1. \(r^1 \le -1\) 且 \(r^2 \le -1\) （两面没有公共部分）
2. \(r^1 \ge 1\) 且 \(r^2 \ge 1\) （两面没有公共部分）
3. \(r^1 = r^2\) （两点投影在同一个点）

下面给出系数\(r^1\)，\(r^2\)计算公式

假设点 \(v_n^{1,1}\) 坐标为 \([x_n^{1,1}, y_n^{1,1}]\)，根据\(v^{1,1}\)与投影点连线与面2直线垂直可得

\[\begin{eqnarray}
\begin{aligned}
& (v_n^{1,1} - v^{1,1})\cdot(v^{2,1} - v^{2,2}) \cr
& = (x_n^{1,1} - x^{1,1})(x^{2,1} - x^{2,2}) + (y_n^{1,1} - y^{1,1})(y^{2,1} - y^{2,2}) = 0
\end{aligned}
\end{eqnarray}\]

将\(v_n^{1,1}\)使用 \(v^{2,1}\) 与 \(v^{2,2}\) 线性表示的表达式代入，整理得方程

\[\begin{equation}
r^1 = \frac{(2x^{1,1} - x^{2,1} - x^{2,2})(x^{2,2} - x^{2,1}) + (2y^{1,1} - y^{2,1} - y^{2,2})(y^{2,2} - y^{2,1})}{(x^{2,2} - x^{2,1})^2 + (y^{2,2} - y^{2,1})^2}
\end{equation}\]

同理，\(r^2\)为

\[\begin{equation}
r^2 = \frac{(2x^{1,2} - x^{2,1} - x^{2,2})(x^{2,2} - x^{2,1}) + (2y^{1,2} - y^{2,1} - y^{2,2})(y^{2,2} - y^{2,1})}{(x^{2,2} - x^{2,1})^2 + (y^{2,2} - y^{2,1})^2}
\end{equation}\]

对应计算过程写为

L   = (x12-x11)^2 + (y12-y11)^2 ;
r21 = ((2*x1-x11-x12)*(x12-x11) + (2*y1-y11-y12)*(y12-y11))/L;
r22 = ((2*x2-x11-x12)*(x12-x11) + (2*y2-y11-y12)*(y12-y11))/L;

再判断之前需要对\(r^1\)，\(r^2\)进行一下处理，其过程如下

% 2.5 Find range of local face coordinate (bracketed between -1 and 1)
r1 = max(-1,min(r21,r22)); r2 = min(1,max(r21,r22));

其含义如下，将投影点线性组合系数限制在 [-1,1] 之间。后面用\(r^1\)，\(r^2\)计算\(v^{1,1}\) 与 \(v^{1,2}\)坐标时，两点不会位于 \(v^{2,1}\) 与 \(v^{2,2}\) 组成线段之外。

根据以上两个条件，对所有边界面进行判断

% 2.6 Compute flag for overlap of b1 face with all other boundary faces
flag = area1+area2+(r1<= -1 & r2<= -1)+(r1>=1 & r2>=1)+(r2-r1<tol);

获得满足条件的边界面序号及总个数

% 2.7 Find other faces with partial matches
matches = setdiff(find(flag < tol),b1);
Nmatches = length(matches(:));

对应面插值矩阵及积分矩阵计算

下面对每个相接的边界面进行计算。首先获得对应面两端的顶点坐标xy11,xy12。

if(Nmatches>0)
    % 3.1 Find matches
    r1 = r1(matches); r2 = r2(matches); 

    % 3.2 Find end points of boundary-boundary intersections
    xy11 = 0.5*[x11;y11]*(1-r1) +  0.5*[x12;y12]*(1+r1);
    xy12 = 0.5*[x11;y11]*(1-r2) +  0.5*[x12;y12]*(1+r2);

每个对应面上循环

% 3.3 For each face-face match
    for n=1:Nmatches

获得对应面单元号与局部面号，储存在结构数组neighbors中

% 3.4 Store which elements intersect
k2 = elmtsB(matches(n)); f2 = facesB(matches(n));
neighbors{sk}.elmtM = k1; neighbors{sk}.faceM = f1;
neighbors{sk}.elmtP = k2; neighbors{sk}.faceP = f2;

根据对应面顶点计算在两面交界面上Gauss点坐标

% 3.5 Build physical Gauss nodes on face fragment
xg = 0.5*(1-gz)*xy11(1,n) + 0.5*(1+gz)*xy12(1,n);
yg = 0.5*(1-gz)*xy11(2,n) + 0.5*(1+gz)*xy12(2,n);

计算Gauss点在两个单元中局部坐标 \((r,s)\)

% 3.6 Find local coordinates of Gauss nodes
[rg1,sg1] = FindLocalCoords2D(k1, xg, yg);
[rg2,sg2] = FindLocalCoords2D(k2, xg, yg);

简要介绍下函数FindLocalCoords2D。在三角形单元中我们知道标准单元与计算单元之间有如下映射关系

\[\begin{equation}
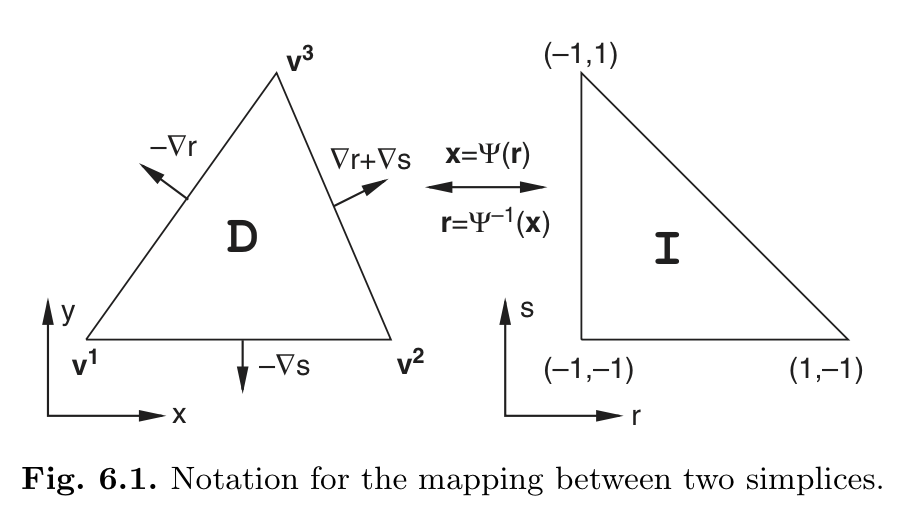
\textbf{x} = -\frac{r+s}{2}v^1 + \frac{r+1}{2}v^2 + \frac{s+1}{2}v^3
\end{equation}\]

因此，若已知三角形内节点坐标 \(\textbf{x} = [x_g, y_g]\) 时，也可利用以上公式反求 \([r,s]\)。

其中 [rg1,sg1] 为Gauss节点在本单元局部坐标，[rg2,sg2] 为Gauss节点在对面单元局部坐标。

在知道局部坐标后，下一步就是计算插值矩阵。每个单元中储存的未知数 \(u\) 是 Lagrange 基函数系数，也可看成是近似解 \(u(x)\) 在 Lagrange 节点上函数值。插值矩阵目的就是根据单元 Lagrange 节点函数值，获得近似解\(u(x)\)在 Gauss 节点处值。

方法很简单，及通过中间基函数（Jacobi基函数）进行准换。已知 Lagrange 基函数与 Jacobi 基函数有以下关系

\[\begin{equation}
V^T \cdot l(x) = P(x)
\end{equation}\]

其中 \(V\) 为Vandermonde 矩阵，对应元素值为

\[\begin{equation}
V_{ij} = P_{j-1}(r_i)
\end{equation}\]

两个基函数系数之间对应关系为

\[\begin{equation}
V \mathbf{ \hat{u} } = \mathbf{u}
\end{equation}\]

注意，若右端系数为Gauss节点近似值\(u_g\)时，对应 Vandermonde 矩阵分量 \(V_g\) 为

\[\begin{equation}
V_{g\{i,j\}} = P_{j-1}(r_{g_i})
\end{equation}\]

因此，插值过程为

1. 将解准换为 Jacobi 基函数系数 \(\mathbf{\hat{u}} = V^{-1} \cdot \mathbf{u}\)
2. 将 Jacobi 基函数系数转换为Gauss点节点值 \(\mathbf{u}_g = V_g \cdot \mathbf{\hat{u}}\)

而插值矩阵即为

\[\begin{equation}
InterpolationMatrix = V_g \cdot V^{-1}
\end{equation}\]

程序中函数InterpMatrix2D负责计算插值矩阵gVM与gVP，两个矩阵分别用于本单元与对应单元插值计算。

% 3.7 Build interpolation matrices for volume nodes ->Gauss nodes
gVM = InterpMatrix2D(rg1,sg1); neighbors{sk}.gVM  = gVM;
gVP = InterpMatrix2D(rg2,sg2); neighbors{sk}.gVP  = gVP;

交接面外法线向量

% 3.8 Find face normal
neighbors{sk}.nx = nx(1+(f1-1)*Nfp,k1);
neighbors{sk}.ny = ny(1+(f1-1)*Nfp,k1);

最后，则是积分矩阵的计算。

在DG-FEM框架中，离散后的边界通量计算公式为

\[\begin{equation}
(JM)^{-1} J_s \int_{\partial \Omega} l(x) F^*_n ds = (JM)^{-1} J_s \sum_{g = 1}^{p} w_g \left( l(x_g) F^*_n(x_g) \right)
\end{equation}\]

这里除了需要计算数值通量在Gauss节点值外（插值矩阵），还需知道 Lagrange 基函数 \(l(x)\) 在Gauss 节点函数值 \(l(x_g)\)。

这里利用如下关系，在单元中

\[\begin{equation}
l(x_g) = (V^T)^{-1} P(x_g)
\end{equation}\]

且矩阵 \(V_g\) 的分量为

\[\begin{equation}
V_{g\{i,j\}} = P_{j-1}(r_{g_i})
\end{equation}\]

那么可以得出

\[\begin{equation}
(V^T)^{-1} \cdot V_g^T = (V^T)^{-1}[P(x_{g_1}), P(x_{g_2}), P(x_{g_3}) \cdots]
=[l(x_{g_1}), l(x_{g_2}), l(x_{g_3}), \cdots]
\end{equation}\]

而 \((V^T)^{-1} \cdot V_g^T\) 恰好为插值矩阵 \(IM\) 的转置。最终

\[\begin{eqnarray}
\begin{aligned}
& \sum_{g = 1}^{p} w_g \left( l(x_g) F^*_n(x_g) \right) = \cr
& [l(x_{g_1}), l(x_{g_2}), l(x_{g_3}), \cdots] \cdot \begin{bmatrix}
w_1 & 0 & 0 & \cdots \cr
0 & w_2 & 0 & \cdots \cr
0 & 0 & w_3 & \cdots \cr
\cdots & \cdots & \cdots & \cdots \cr
\end{bmatrix}
\begin{bmatrix}
F_n^*(x_{g_1}) \cr
F_n^*(x_{g_2}) \cr
\cdots \cr
F_n^*(x_{g_n}) \cr
\end{bmatrix} \cr
& = (V^T)^{-1} \cdot V_g^T \cdot diag(w_i) \cdot F^*_n
\end{aligned}
\end{eqnarray}\]

其中

\[\begin{equation}
l(x_{g_i}) = \begin{bmatrix}
l_0(x_{g_i}) \cr
l_1(x_{g_i}) \cr
\cdots \cr
l_{p-1}(x_{g_i}) \cr
\end{bmatrix}
\end{equation}\]

即，除了右端通量 \(F^*_n(x_g)\) 外，其余系数写为矩阵形式为

% 4.0 Build partial face data lift operator

% 4.1 Compute weights for lifting
partsJ = sqrt( (xy11(1,n)-xy12(1,n))^2 + (xy11(2,n)-xy12(2,n))^2 )/2;
dgw = gw*partsJ/J(1,k1); 

% 4.2 Build matrix to lift Gauss data to volume data
neighbors{sk}.lift = V*V'*(gVM')*diag(dgw);

最终，结构数组neighbours储存了所有non-conforming对应面计算所需条件，包括

1. 两边单元号与面局部序号
2. 外法向向量
3. 对应面两边单元插值到Gauss节点插值矩阵
4. 边界积分质量矩阵

在计算时，首先略去non-conforming对应面之间数值通量传递，在计算完其他普通单元后开始循环计算non-conforming对应面之间边界数值通量积分，直到把所有面计算一遍。