「JOI 2014 Final」裁剪线

做法一

首先将边界也视作四条裁剪线，整个平面作为一张纸，视存在 \(y = -\infty, y = +\infty, x = -\infty, x = +\infty\) 四条直线。

按照纵坐标依次扫描每条线，每次维护当前纵坐标水平无穷长的直线和每个位置下面第一条之前插入过的纵坐标之间围成区域的连通性，如下图所示：

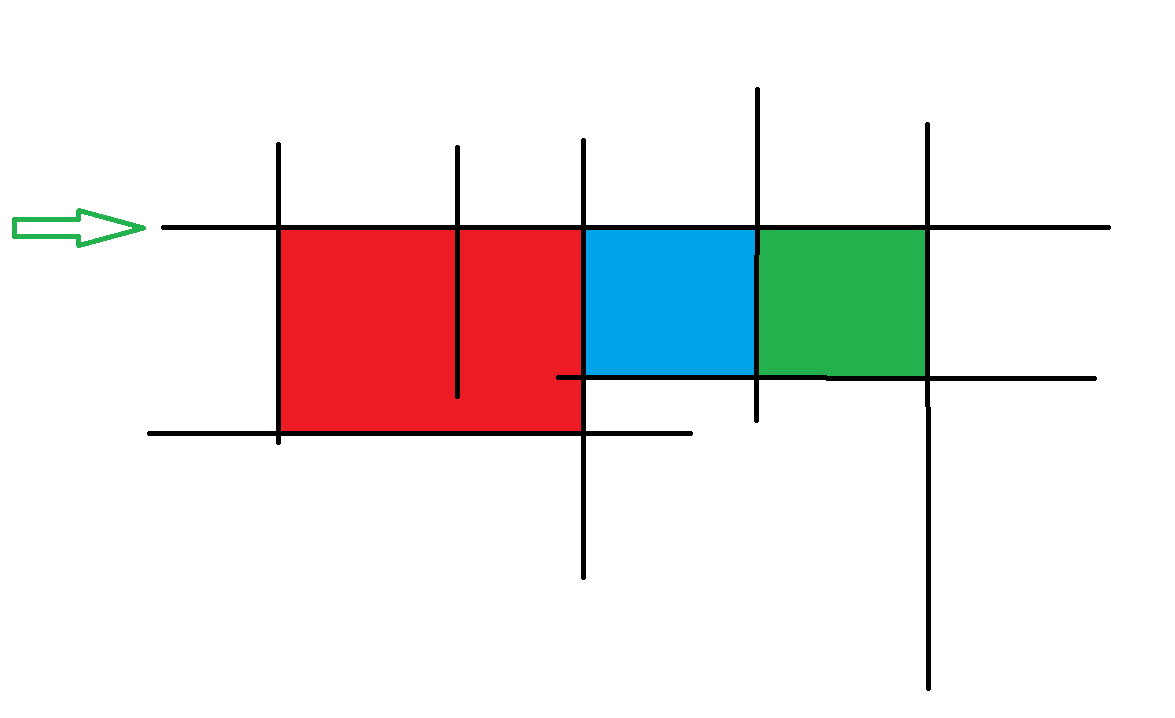
图中箭头指向的就是当前扫描（维护）到的（水平）线，红绿蓝分别为所围成的区域（有效）。

具体地，由于上述扫描过程中连通性只会在：水平线段，竖直线段底部，竖直线段顶部发生改变，因此我们将这些位置按照纵坐标排序依次考虑。

同时，为了方便我们直接让每条竖直线段管辖其右边第一个区域和其他区域的连通性。

• 竖直线段底部

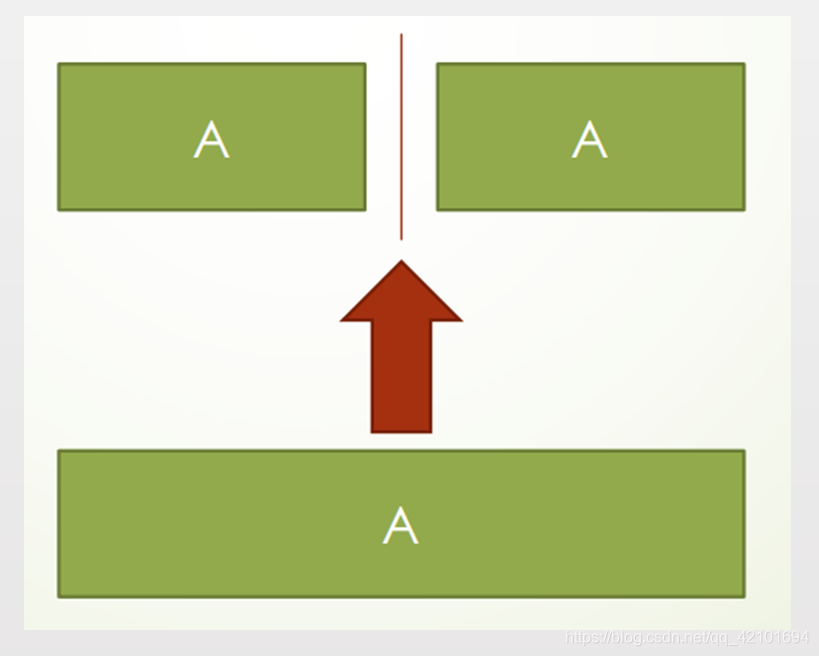
将原本一整段区域分成了两段，考虑对新加入的竖直线段新建一个区域，其余左边最近的区域联通，那么在并查集上连边。

• 竖直线段顶部

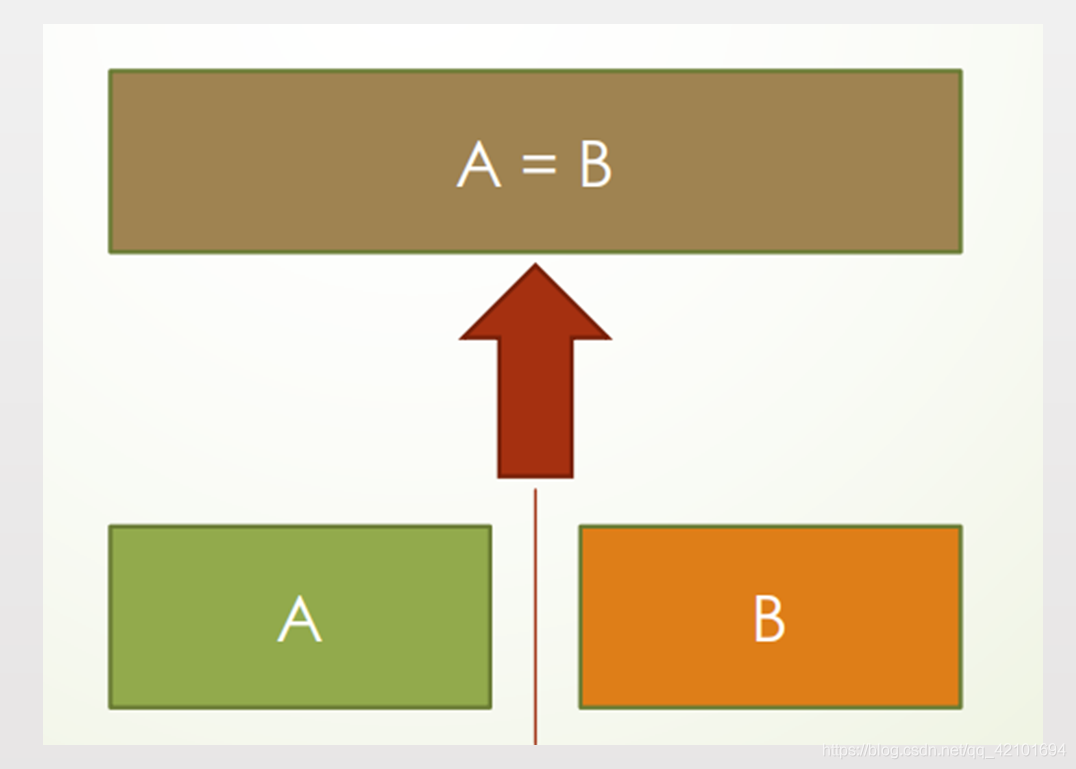
无论如何，只需要将左右两个区域在并查集上联通即可。

• 水平线段

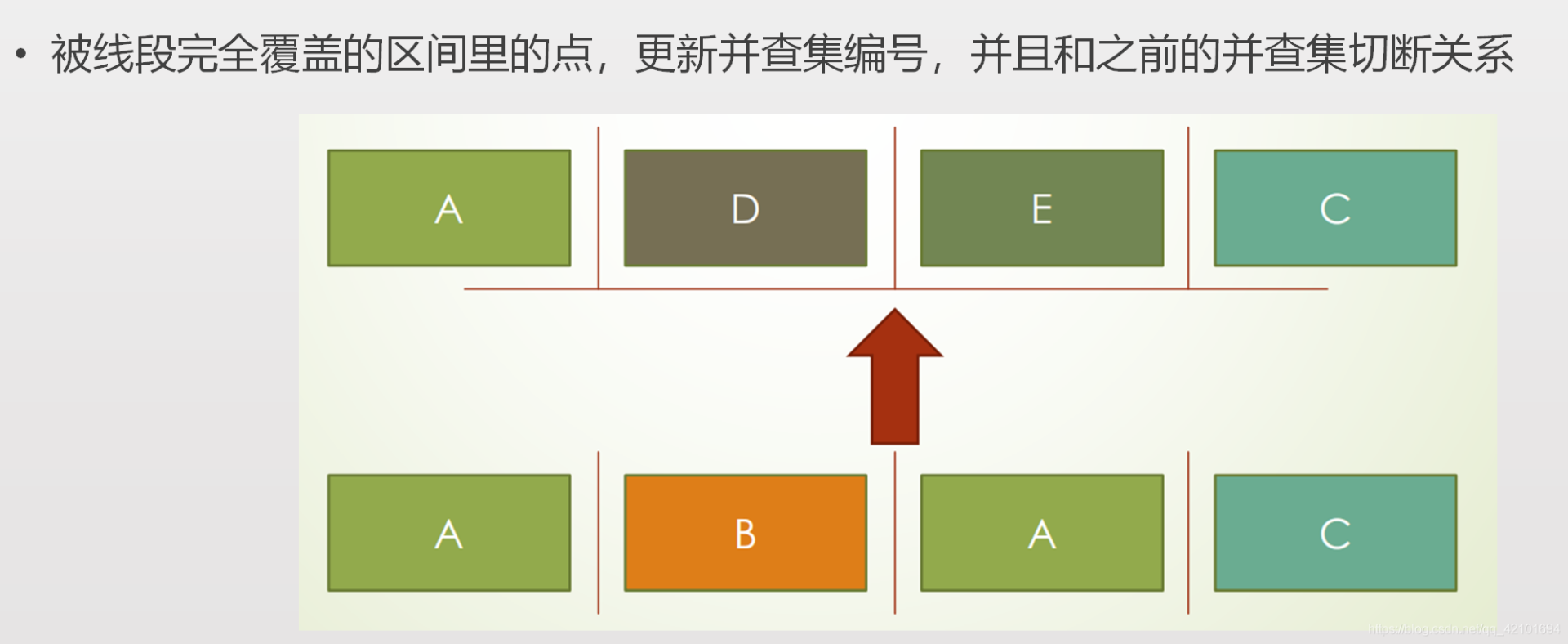
加入水平线段后，中间被完全覆盖的区域与外界且两两之间不连通，需要赋予全新的并查集编号，这里显然不能暴力，考虑用数据结构维护。

首先对于竖直线段我们要支持插入，删除，查询前驱，平衡树显然可以直接胜任。

水平线段需要整个区域打上重新标号的懒标记，下次再进行横向覆盖的时候，整个区间存在懒标记的节点接下来一定都不会与外界联通需要直接加入答案，因此平衡树上还需要维护区间内懒标记没有被释放的点的数量。

最后我们再统计所有区域在并查集节点中构成的连通块数量加入答案即可。

因为有查询前驱操作，所以可以事先插入 \(x = -\infty\) 这条直线，最后答案需要减一。

注意在下传懒标记的时候只需要新建点而不需要在并查集上连边，时空复杂度均为 \(\mathcal{O}(n \log n)\).

做法二

注意到本题是网格图的一部分，那么一定是一张平面图，考虑利用欧拉公式求平面图面的数量。

注意本题可能不连通，设交点数量为 \(V\)，线段 数（不是交点之间的边数！）为 \(E\)，面数为 \(F\)，线段 联通块（不是交点连通块个数）个数为 \(C\).

之所以和欧拉定理设的不同是因为统计线段连通块数比交点连通块数好做，原本交点间边数和交点连通块个数差可以抵掉一部分变为 \(E, C\) 之间的关系，即：

\[V - E - F + C = -1
\]

那么只需要求出 \(V, E, C\) 即可，\(E\) 显然是好求的，\(V\) 是经典扫描线问题，考虑如何求 \(C\).

依然考虑扫描线，沿水平从下往上扫描，每次相当于支持加删竖直线段，将水平线段和一个区间内的竖直线段连边。

考虑线段树优化区间连边，我们把每个竖直线段插入到线段树上对应的 \(\log\) 个区间，每次水平线段找到区间在线段树上 \(\log\) 个子区间。

注意到整个区间内的点如果全部和一个点联通那么这些点都是联通的，我们只需要保留一个代表节点即可。

很显然，代表节点就是顶端纵坐标最大的点，这样可以保证正确性。

复杂度与做法一的复杂度相同但思维难度降低了。