梯度下降法实现（Python语言描述）

原文地址：传送门

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

plt.style.use(['ggplot'])

当你初次涉足机器学习时，你学习的第一个基本算法就是 梯度下降 (Gradient Descent), 可以说梯度下降法是机器学习算法的支柱。 在这篇文章中，我尝试使用

p

y

t

h

o

n

python

python 解释梯度下降法的基本原理。一旦掌握了梯度下降法，很多问题就会变得容易理解，并且利于理解不同的算法。

如果你想尝试自己实现梯度下降法， 你需要加载基本的

p

y

t

h

o

n

python

python

p

a

c

k

a

g

e

s

packages

packages ——

n

u

m

p

y

numpy

numpy and

m

a

t

p

l

o

t

l

i

b

matplotlib

matplotlib

首先， 我们将创建包含着噪声的线性数据

# 随机创建一些噪声
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

接下来通过 matplotlib 可视化数据

# 可视化数据
plt.plot(X, y, 'b.')
plt.xlabel("$x$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([0, 2, 0, 15])

显然，

y

y

y 与

x

x

x 具有良好的线性关系，这个数据非常简单，只有一个自变量

x

x

x.

我们可以将其表示为简单的线性关系：

y

=

b

+

m

x

y = b + mx

y=b+mx

并求出

b

b

b ,

m

m

m。

这种被称为解方程的分析方法并没有什么不妥，但机器学习是涉及矩阵计算的，因此我们使用矩阵法（向量法）进行分析。

我们将

y

y

y 替换成

J

(

θ

)

J(\theta)

J(θ)，

b

b

b 替换成

θ

0

\theta_0

θ0​，

m

m

m 替换成

θ

1

\theta_1

θ1​。
得到如下表达式：

J

(

θ

)

=

θ

0

+

θ

1

x

J(\theta) = \theta_0 + \theta_1 x

J(θ)=θ0​+θ1​x

注意： 本例中

θ

0

=

4

\theta_0= 4

θ0​=4，

θ

1

=

3

\theta_1= 3

θ1​=3

求解

θ

0

\theta_0

θ0​ 和

θ

1

\theta_1

θ1​ 的分析方法，代码如下：

X_b = np.c_[np.ones((100, 1)), X] # 为X添加了一个偏置单位，对于X中的每个向量都是1
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
theta_best

array([[3.86687149],
       [3.12408839]])

不难发现这个值接近真实的

θ

0

\theta_0

θ0​，

θ

1

\theta_1

θ1​，由于我在数据中引入了噪声，所以存在误差。

X_new = np.array([[0], [2]])
X_new_b = np.c_[np.ones((2, 1)), X_new]
y_predict = X_new_b.dot(theta_best)
y_predict

array([[ 3.86687149],
       [10.11504826]])

梯度下降法 （Gradient Descent）

Cost Function & Gradients

计算代价函数和梯度的公式如下所示。

注意：代价函数用于线性回归，对于其他算法，代价函数是不同的，梯度必须从代价函数中推导出来。

Cost

J

(

θ

)

=

1

/

2

m

∑

i

=

1

m

(

h

(

θ

)

(

i

)

−

y

(

i

)

)

2

J(\theta) = 1/2m \sum_{i=1}^{m} (h(\theta)^{(i)} - y^{(i)})^2

J(θ)=1/2mi=1∑m​(h(θ)(i)−y(i))2

Gradient

∂

J

(

θ

)

∂

θ

j

=

1

/

m

∑

i

=

1

m

(

h

(

θ

(

i

)

−

y

(

i

)

)

.

X

j

(

i

)

\frac{\partial J(\theta)}{\partial \theta_j} = 1/m\sum_{i=1}^{m}(h(\theta^{(i)} - y^{(i)}).X_j^{(i)}

∂θj​∂J(θ)​=1/mi=1∑m​(h(θ(i)−y(i)).Xj(i)​

Gradients

θ

0

:

=

θ

0

−

α

.

(

1

/

m

.

∑

i

=

1

m

(

h

(

θ

(

i

)

−

y

(

i

)

)

.

X

0

(

i

)

)

\theta_0: = \theta_0 -\alpha . (1/m .\sum_{i=1}^{m}(h(\theta^{(i)} - y^{(i)}).X_0^{(i)})

θ0​:=θ0​−α.(1/m.i=1∑m​(h(θ(i)−y(i)).X0(i)​)

θ

1

:

=

θ

1

−

α

.

(

1

/

m

.

∑

i

=

1

m

(

h

(

θ

(

i

)

−

y

(

i

)

)

.

X

1

(

i

)

)

\theta_1: = \theta_1 -\alpha . (1/m .\sum_{i=1}^{m}(h(\theta^{(i)} - y^{(i)}).X_1^{(i)})

θ1​:=θ1​−α.(1/m.i=1∑m​(h(θ(i)−y(i)).X1(i)​)

θ

2

:

=

θ

2

−

α

.

(

1

/

m

.

∑

i

=

1

m

(

h

(

θ

(

i

)

−

y

(

i

)

)

.

X

2

(

i

)

)

\theta_2: = \theta_2 -\alpha . (1/m .\sum_{i=1}^{m}(h(\theta^{(i)} - y^{(i)}).X_2^{(i)})

θ2​:=θ2​−α.(1/m.i=1∑m​(h(θ(i)−y(i)).X2(i)​)

θ

j

:

=

θ

j

−

α

.

(

1

/

m

.

∑

i

=

1

m

(

h

(

θ

(

i

)

−

y

(

i

)

)

.

X

0

(

i

)

)

\theta_j: = \theta_j -\alpha . (1/m .\sum_{i=1}^{m}(h(\theta^{(i)} - y^{(i)}).X_0^{(i)})

θj​:=θj​−α.(1/m.i=1∑m​(h(θ(i)−y(i)).X0(i)​)

def cal_cost(theta, X, y):
    '''
    Calculates the cost for given X and Y. The following shows and example of a single dimensional X
    theta = Vector of thetas
    X     = Row of X's np.zeros((2,j))
    y     = Actual y's np.zeros((2,1))
    where:
        j is the no of features
    '''
    m = len(y)
    predictions = X.dot(theta)
    cost = (1/2*m) * np.sum(np.square(predictions - y))
    return cost

def gradient_descent(X, y, theta, learning_rate = 0.01, iterations = 100):
    '''
    X    = Matrix of X with added bias units
    y    = Vector of Y
    theta=Vector of thetas np.random.randn(j,1)
    learning_rate
    iterations = no of iterations
    Returns the final theta vector and array of cost history over no of iterations
    '''
    m = len(y)
    # learning_rate = 0.01
    # iterations = 100
    cost_history = np.zeros(iterations)
    theta_history = np.zeros((iterations, 2))
    for i in range(iterations):
        prediction = np.dot(X, theta)
        theta = theta - (1/m) * learning_rate * (X.T.dot((prediction - y)))
        theta_history[i, :] = theta.T
        cost_history[i] = cal_cost(theta, X, y)
    return theta, cost_history, theta_history

# 从1000次迭代开始，学习率为0.01。从高斯分布的θ开始
lr =0.01
n_iter = 1000
theta = np.random.randn(2, 1)
X_b = np.c_[np.ones((len(X), 1)), X]
theta, cost_history, theta_history = gradient_descent(X_b, y, theta, lr, n_iter)
print('Theta0:          {:0.3f},\nTheta1:          {:0.3f}'.format(theta[0][0],theta[1][0]))
print('Final cost/MSE:  {:0.3f}'.format(cost_history[-1]))

Theta0:          3.867,
Theta1:          3.124
Final cost/MSE:  5457.747

# 绘制迭代的成本图
fig, ax = plt.subplots(figsize=(12,8))
ax.set_ylabel('J(Theta)')
ax.set_xlabel('Iterations')
ax.plot(range(1000), cost_history, 'b.')

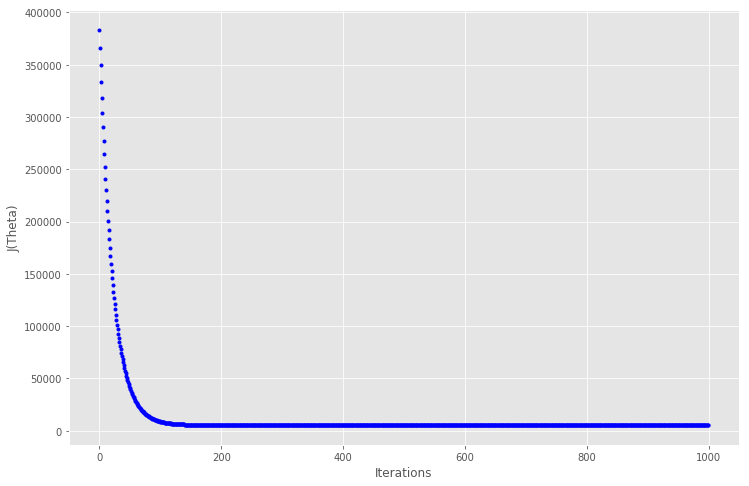
在大约 150 次迭代之后代价函数趋于稳定，因此放大到迭代200，看看曲线

fig, ax = plt.subplots(figsize=(10,8))
ax.plot(range(200), cost_history[:200], 'b.')

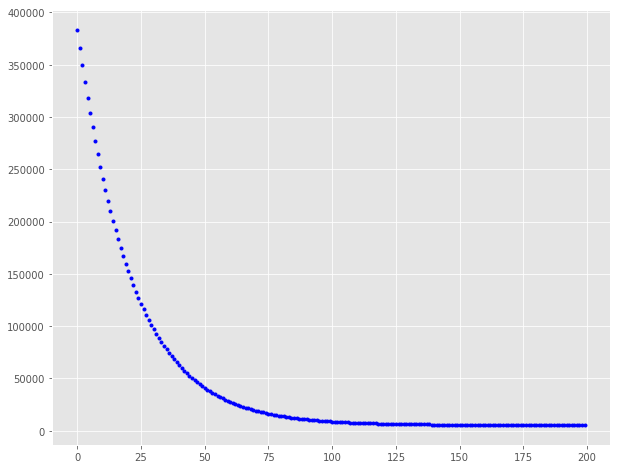
值得注意的是，最初成本下降得更快，然后成本降低的收益就不那么多了。 我们可以尝试使用不同的学习速率和迭代组合，并得到不同学习率和迭代的效果会如何。

让我们建立一个函数，它可以显示效果，也可以显示梯度下降实际上是如何工作的。

def plot_GD(n_iter, lr, ax, ax1=None):
    '''
    n_iter = no of iterations
    lr = Learning Rate
    ax = Axis to plot the Gradient Descent
    ax1 = Axis to plot cost_history vs Iterations plot
    '''
    ax.plot(X, y, 'b.')
    theta = np.random.randn(2, 1)
    tr = 0.1
    cost_history = np.zeros(n_iter)
    for i in range(n_iter):
        pred_prev = X_b.dot(theta)
        theta, h, _ = gradient_descent(X_b, y, theta, lr, 1)
        pred = X_b.dot(theta)
        cost_history[i] = h[0]
        if ((i % 25 == 0)):
            ax.plot(X, pred, 'r-', alpha=tr)
            if tr < 0.8:
                tr += 0.2
    if not ax1 == None:
        ax1.plot(range(n_iter), cost_history, 'b.')

# 绘制不同迭代和学习率组合的图
fig = plt.figure(figsize=(30,25), dpi=200)
fig.subplots_adjust(hspace=0.4, wspace=0.4)
it_lr = [(2000, 0.001), (500, 0.01), (200, 0.05), (100, 0.1)]
count = 0
for n_iter, lr in it_lr:
    count += 1
    ax = fig.add_subplot(4, 2, count)
    count += 1
    ax1 = fig.add_subplot(4, 2, count)
    ax.set_title("lr:{}" .format(lr))
    ax1.set_title("Iterations:{}" .format(n_iter))
    plot_GD(n_iter, lr, ax, ax1)

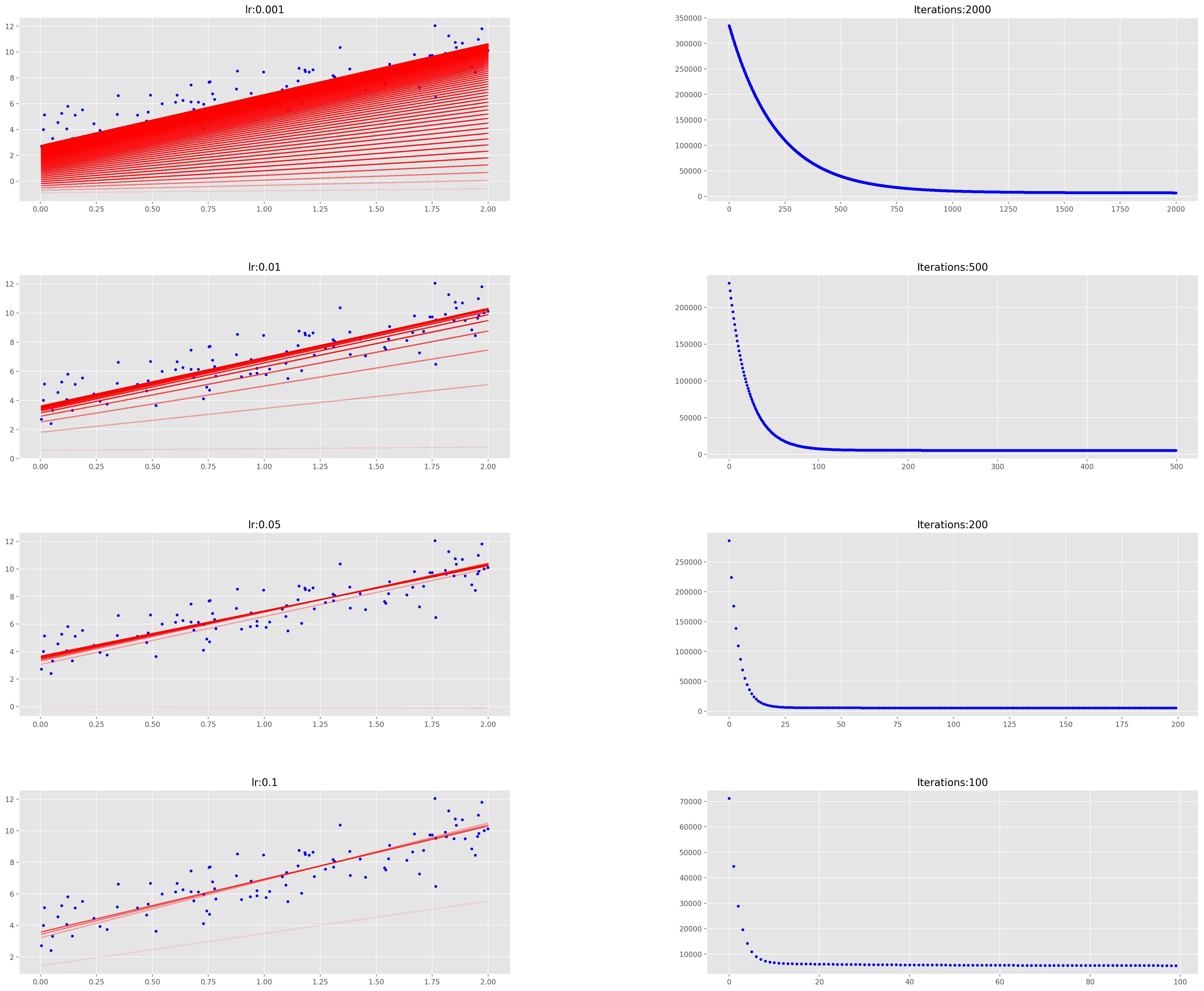
通过观察发现，以较小的学习速率收集解决方案需要很长时间，而学习速度越大，学习速度越快。

_, ax = plt.subplots(figsize=(14, 10))
plot_GD(100, 0.1, ax)

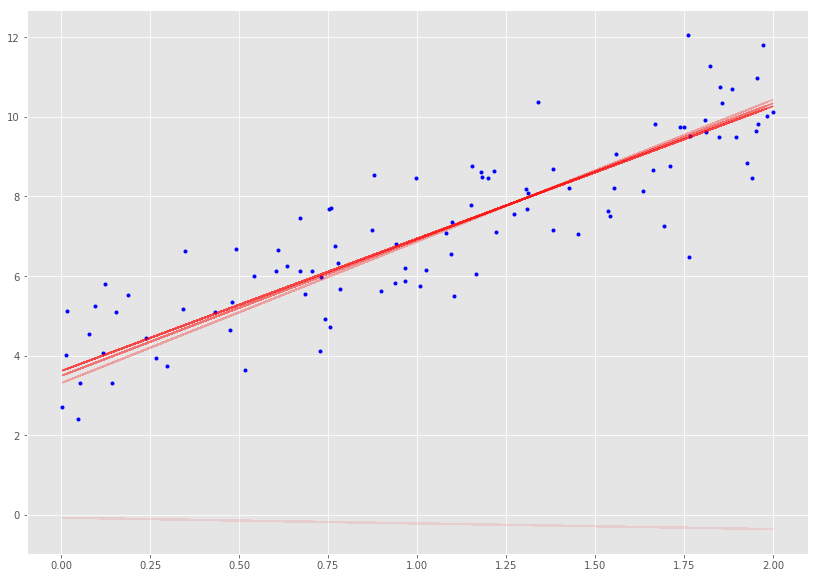
随机梯度下降法（Stochastic Gradient Descent）

随机梯度下降法，其实和批量梯度下降法原理类似，区别在与求梯度时没有用所有的

m

m

m 个样本的数据，而是仅仅选取一个样本

j

j

j 来求梯度。对应的更新公式是：

θ

i

=

θ

i

−

α

(

h

θ

(

x

0

(

j

)

,

x

1

(

j

)

,

.

.

.

x

n

(

j

)

)

−

y

j

)

x

i

(

j

)

\theta_i = \theta_i - \alpha (h_\theta(x_0^{(j)}, x_1^{(j)}, ...x_n^{(j)}) - y_j)x_i^{(j)}

θi​=θi​−α(hθ​(x0(j)​,x1(j)​,...xn(j)​)−yj​)xi(j)​

def stocashtic_gradient_descent(X, y, theta, learning_rate=0.01, iterations=10):
    '''
    X    = Matrix of X with added bias units
    y    = Vector of Y
    theta=Vector of thetas np.random.randn(j,1)
    learning_rate
    iterations = no of iterations
    Returns the final theta vector and array of cost history over no of iterations
    '''
    m = len(y)
    cost_history = np.zeros(iterations)
    for it in range(iterations):
        cost = 0.0
        for i in range(m):
            rand_ind = np.random.randint(0, m)
            X_i = X[rand_ind, :].reshape(1, X.shape[1])
            y_i = y[rand_ind, :].reshape(1, 1)
            prediction = np.dot(X_i, theta)
            theta -= (1/m) * learning_rate * (X_i.T.dot((prediction - y_i)))
            cost += cal_cost(theta, X_i, y_i)
        cost_history[it] = cost
    return theta, cost_history

lr = 0.5
n_iter = 50
theta = np.random.randn(2,1)
X_b = np.c_[np.ones((len(X),1)), X]
theta, cost_history = stocashtic_gradient_descent(X_b, y, theta, lr, n_iter)
print('Theta0:          {:0.3f},\nTheta1:          {:0.3f}' .format(theta[0][0],theta[1][0]))
print('Final cost/MSE:  {:0.3f}' .format(cost_history[-1]))

Theta0:          3.762,
Theta1:          3.159
Final cost/MSE:  46.964

fig, ax = plt.subplots(figsize=(10,8))
ax.set_ylabel('$J(\Theta)$' ,rotation=0)
ax.set_xlabel('$Iterations$')
theta = np.random.randn(2,1)
ax.plot(range(n_iter), cost_history, 'b.')

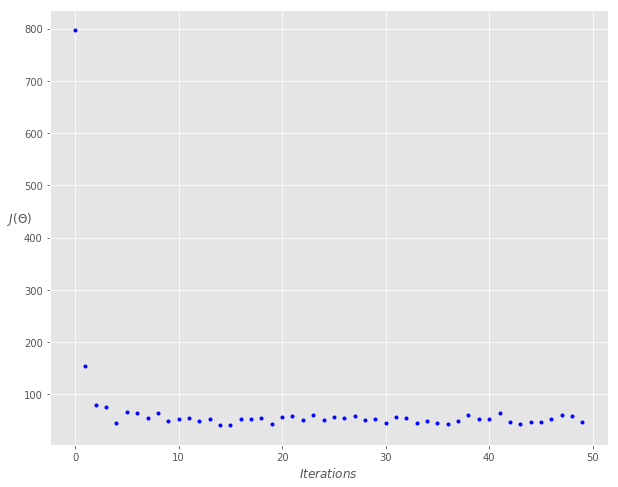
小批量梯度下降法（Mini-batch Gradient Descent）

小批量梯度下降法是批量梯度下降法和随机梯度下降法的折衷，也就是对于

m

m

m 个样本，我们采用x个样子来迭代，

1

<

x

<

m

1<x<m

1<x<m。一般可以取

x

=

10

x=10

x=10，当然根据样本的数据，可以调整这个

x

x

x 的值。对应的更新公式是：

θ

i

=

θ

i

−

α

∑

j

=

t

t

+

x

−

1

(

h

θ

(

x

0

(

j

)

,

x

1

(

j

)

,

.

.

.

x

n

(

j

)

)

−

y

j

)

x

i

(

j

)

\theta_i = \theta_i - \alpha \sum\limits_{j=t}^{t+x-1}(h_\theta(x_0^{(j)}, x_1^{(j)}, ...x_n^{(j)}) - y_j)x_i^{(j)}

θi​=θi​−αj=t∑t+x−1​(hθ​(x0(j)​,x1(j)​,...xn(j)​)−yj​)xi(j)​

def minibatch_gradient_descent(X, y, theta, learning_rate=0.01, iterations=10, batch_size=20):
    '''
    X    = Matrix of X without added bias units
    y    = Vector of Y
    theta=Vector of thetas np.random.randn(j,1)
    learning_rate
    iterations = no of iterations
    Returns the final theta vector and array of cost history over no of iterations
    '''
    m = len(y)
    cost_history = np.zeros(iterations)
    n_batches = int(m / batch_size)
    for it in range(iterations):
        cost = 0.0
        indices = np.random.permutation(m)
        X = X[indices]
        y = y[indices]
        for i in range(0, m, batch_size):
            X_i = X[i: i+batch_size]
            y_i = y[i: i+batch_size]
            X_i = np.c_[np.ones(len(X_i)), X_i]
            prediction = np.dot(X_i, theta)
            theta -= (1/m) * learning_rate * (X_i.T.dot((prediction - y_i)))
            cost += cal_cost(theta, X_i, y_i)
        cost_history[it] = cost
    return theta, cost_history

lr = 0.1
n_iter = 200
theta = np.random.randn(2, 1)
theta, cost_history = minibatch_gradient_descent(X, y, theta, lr, n_iter)
print('Theta0:          {:0.3f},\nTheta1:          {:0.3f}' .format(theta[0][0], theta[1][0]))
print('Final cost/MSE:  {:0.3f}' .format(cost_history[-1]))

Theta0:          3.842,
Theta1:          3.146
Final cost/MSE:  1090.518

fig, ax = plt.subplots(figsize=(10,8))
ax.set_ylabel('$J(\Theta)$', rotation=0)
ax.set_xlabel('$Iterations$')
theta = np.random.randn(2, 1)
ax.plot(range(n_iter), cost_history, 'b.')

参考：

• Gradient Descent in Python
• 梯度下降（Gradient Descent）小结