普里姆算法（Prim）

概览

普里姆算法（Prim算法），图论中的一种算法，可在加权连通图（带权图）里搜索最小生成树。即此算法搜索到的边（Edge）子集所构成的树中，不但包括了连通图里的所有顶点（Vertex）且其所有边的权值之和最小。（注：N个顶点的图中，其最小生成树的边为N-1条，且各边之和最小。树的每一个节点（除根节点）有且只有一个前驱，所以，只有N-1条边。）

该算法于1930年由捷克数学家沃伊捷赫·亚尔尼克（Vojtěch Jarník）发现；并在1957年由美国计算机科学家罗伯特·普里姆（Robert C. Prim）独立发现；1959年，艾兹格·迪科斯彻再次发现了该算法。因此，在某些场合，普里姆算法又被称为DJP算法、亚尔尼克算法或普里姆－亚尔尼克算法。

定义

假设G=(V, {E})是连通网，TE是N上最小生成树中边（Edge）的集合。V是图G的顶点的集合，E是图G的边的集合。算法从U={u₀} (u₀∈V)，TE={}开始。重复执行下述操作：

• 在所有u∈U，v∈V-U的边(u, v)∈E中找一条代价（权值）最小的边(u₀, v₀)并入集合TE。
• 同时v₀并入U
• 直至U=V为止。此时TE中必有n-1条边，则T=(V, {TE})为N的最小生成树。

由算法代码中的循环嵌套可得知此算法的时间复杂度为O(n²)。

过程简述

输入：带权连通图（网）G，其顶点的集合为V，边的集合为E。

初始：U={u}，u为从V中任意选取顶点，作为起始点；TE={}。

操作：重复以下操作，直到U=V，即两个集合相等。

• 在集合E中选取权值最小的边(u, v)，u∈U，v∈V且v∉U。（如果存在多条满足前述条件，即权值相同的边，则可任意选取其中之一。）
• 将v并入U，将(u, v)边加入TE。

输出：用集合U和TE来描述所得到的最小生成树

如何实现

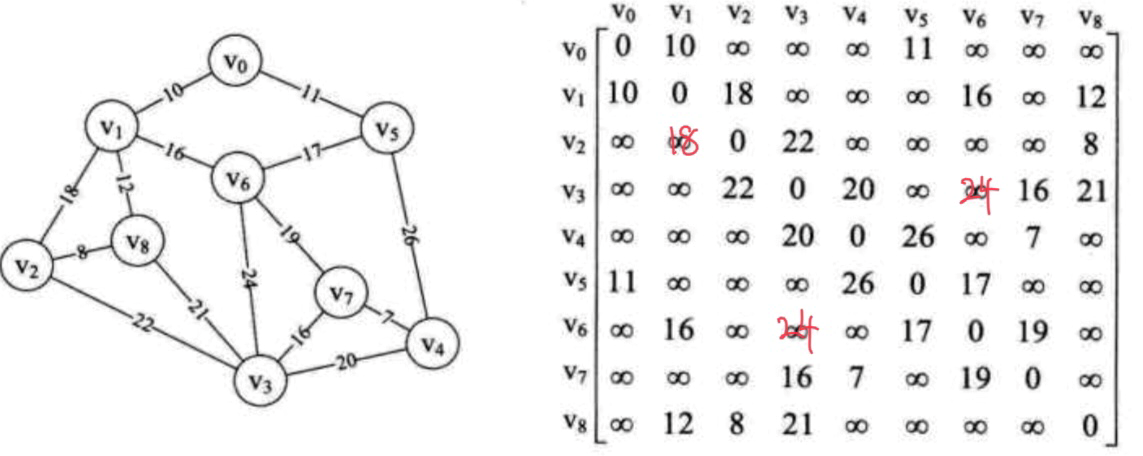
如上面的这个图G=(V, {E})，其中V={v₀, v₁, v₂, v₃, v₄, v₅, v₆, v₇, v₈}，E= {(v₀, v₁), (v₀, v₅), (v₁, v₆), (v₅, v₆), (v₁, v₈), (v₁, v₂), (v₂, v₈), (v₆, v₇), (v₃, v₆), (v₄, v₅), (v₄, v₇), (v₃, v₇), (v₃, v₄), (v₃,v₈), (v₂, v₃)}

用邻接矩阵来表示该图G，得上图右边的一个邻接矩阵。

此带权连通图G有n=9个顶点，其最小生成树则必有n-1=8条边。（注意：图G的最小生成树是一棵树，且图G中的每个顶点都在这棵树里，故必含有n个顶点；而除树根节点，每个节点有且只有一个前驱，所以图G的最小生成树有且只有n-1条边。若边数大于n-1，则必有树中某个顶点与另一个顶点存在第二条边，从而不能构成树。树中节点是一对多关系而不是多对多关系。）

①输入：带权连通图G=(V, {E})，求图G的最小生成树。

②初始：U={u}，取图G中的v₀作为u，用数组adjVex=int[9]来表示U（最终U要等于V），adjVex数组记录的是U中顶点的下标。U是最小生成树T的各边的起始顶点的集合。

adjVex初始值为[0, 0, 0, 0, 0, 0, 0, 0, 0]，表示从顶点v₀开始去寻找权值最小的边。

用数组lowCost=int[9] 表示adjVex中各点到集合V中顶点构成的边的权值。lowCost数组中元素的索引即是顶点V的下标。解释：adjVex[3]==0，表示v₀，adjVex[5]==0，表示v₀。lowCost[3]==∞且adjVex[3]==0，表示(v₀, v₃)边不存在；lowCost[5]==11且adjVex[5]==0，表示(v₀, v₅)边的权值为11。

如：邻接矩阵中的v₀行，v₀顶点与各顶点构成的边及其权值用下面这的方式表示：

示例一

索引：index  [0,  1, 2, 3, 4,  5, 6, 7, 8]

权值：lowCost[0, 10, ∞, ∞, ∞, 11, ∞, ∞, ∞]

下标：adjVex [0,  0, 0, 0, 0,  0, 0, 0, 0]

(v₀, v₀, 0), (v₀, v₃, ∞), (v₀, v₅, 11) 

0表示以该顶点为终点的边已经并入图G的最小生成树的边集合——TE集合，不需要再比较（搜索）。

∞表示以该顶点为终点的边不存在。

③操作：

1.上面示例一中，最小的权值为10，此时lowCost中下标k=1，相应地adjVex[k]即adjVex[1]==0，记录下此时的边为(v₀, v₁)。

2.将adjVex[k]即adjVex[1]设为1，表示将顶点v₁放入图G的最小生成树的顶点集合U中。

3.将lowCost[k]即lowCost[1]设为0，表示以v₁为终止点的边已搜索。

4.然后，将焦点转向顶点v₁，看看从v₁开始的边有哪些是权值小于从之前的顶点v₀开始的边的。此时k==1。则有以下过程：

索引：index  [ 0,  1, 2, 3, 4,  5, 6, 7, 8]

权值：lowCost[ 0,  0, ∞, ∞, ∞, 11, ∞, ∞, ∞]

下标：adjVex [ 0,  1, 0, 0, 0,  0, 0, 0, 0]

顶点：vex[1] [10,  0,18, ∞, ∞,  ∞,16, ∞,12]

由于lowCost[0]和lowCost[1]为0，所以从lowCost[2]开始比较权值。vex[1][2]==18 < lowCost[2]，意思是(v₀, v₂)==∞不存在这条边，(v₁, v₂)==18，存在权为18的边(v₁, v₂)，类似的还有vex[1][6]==16 < lowCost[6]和vex[1][8]==12 < lowCost[8]。

把k==1赋值给

adjVex[2]、adjVex[6]和adjVex[8]。

把权值18、16和12赋值给

lowCost[2]、lowCost[6]和lowCost[8]。

更新后的权值数组和邻接顶点数组如下：

索引：index  [ 0,1,  2, 3, 4,  5,  6, 7,  8]

权值：lowCost[ 0, 0, 18, ∞, ∞, 11, 16, ∞, 12]

下标：adjVex [ 0, 1,  1, 0, 0,  0,  1, 0,  1]

故下次循环从顶点v₁为起点去搜索lowCost中权值最小的边。如此往复循环，直到图G中的每一个顶点都被遍历到。（邻接矩阵的每一行都被遍历到）

④输出：

演示过程

Loop 1

lowCost: [ 0, 10, ∞, ∞, ∞, 11, ∞, ∞, ∞ ]

adjVex: [ 0,  0, 0, 0, 0,  0, 0, 0, 0 ]

lowCost: [ 0, 0, 18, ∞, ∞, 11, 16, ∞, 12 ]

adjVex: [ 0, 1,  1, 0, 0,  0,  1, 0,  1 ]

Loop 2

lowCost: [ 0, 0, 18, ∞, ∞, 11, 16, ∞, 12 ]

adjVex: [ 0, 1,  1, 0, 0,  0,  1, 0,  1 ]

lowCost: [ 0, 0, 18, ∞, 26, 0, 16, ∞, 12 ]

adjVex: [ 0, 1,  5, 0,  5, 0, 1, 0, 1 ]

Loop 3

lowCost: [ 0, 0, 18, ∞, 26, 0, 16, ∞, 12 ]

adjVex: [ 0, 1,  5, 0,  5, 0,  1, 0,  1 ]

lowCost: [ 0, 0, 8, 21, 26, 0, 16, ∞, 0 ]

adjVex: [ 0, 1, 8,  8,  5, 0,  1, 0, 1 ]

Loop 4

lowCost: [ 0, 0, 8, 21, 26, 0, 16, ∞, 0 ]

adjVex: [ 0, 1, 8,  8,  5, 0,  1, 0, 1 ]

lowCost: [ 0, 0, 0, 21, 26, 0, 16, ∞, 0 ]

adjVex: [ 0, 1, 8,  8,  2, 0,  1, 0, 1 ]

Loop 5

lowCost: [ 0, 0, 0, 21, 26, 0, 16, ∞, 0 ]

adjVex: [ 0, 1, 8,  8,  2, 0,  1, 0, 1 ]

lowCost: [ 0, 0, 0, 21, 26, 0, 0, 19, 0 ]

adjVex: [ 0, 1, 8,  8,  2, 6, 1,  6, 1 ]

Loop 6

lowCost: [ 0, 0, 0, 21, 26, 0, 0, 19, 0 ]

adjVex: [ 0, 1, 8,  8,  2, 6, 1,  6, 1 ]

lowCost: [ 0, 0, 0, 16, 7, 0, 0, 0, 0 ]

adjVex: [ 0, 1, 8,  7, 7, 6, 7, 6, 1 ]

Loop 7

lowCost: [ 0, 0, 0, 16, 7, 0, 0, 0, 0 ]

adjVex: [ 0, 1, 8, 7,  7, 6, 7, 6, 1 ]

lowCost: [ 0, 0, 0, 16, 0, 0, 0, 0, 0 ]

adjVex: [ 0, 1, 8,  7, 7, 6, 7, 4, 1 ]

Loop 8

lowCost: [ 0, 0, 0, 16, 0, 0, 0, 0, 0 ]

adjVex: [ 0, 1, 8,  7, 7, 6, 7, 4, 1 ]

lowCost: [ 0, 0, 0, 0, 0, 0, 0, 0, 0 ]

adjVex: [ 0, 1, 8, 7, 7, 6, 7, 4, 3 ]

运行结果

(0, 1)

(0, 5)

(1, 8)

(8, 2)

(1, 6)

(6, 7)

(7, 4)

(7, 3)

算法代码

using System;

namespace Prim

{

class Program

{

static void Main(string[] args)

{

int numberOfVertexes = 9,

infinity = int.MaxValue;

int[][] graph = new int[][] {

new int[]{0, 10, infinity, infinity, infinity, 11, infinity, infinity, infinity },

new int[]{ 10, 0, 18, infinity, infinity, infinity, 16, infinity, 12 },

new int[]{ infinity, 18, 0, 22, infinity, infinity, infinity, infinity, 8 },

new int[]{ infinity, infinity, 22, 0, 20, infinity, 24, 16, 21 },

new int[]{ infinity, infinity, infinity, 20, 0, 26, infinity, 7, infinity },

new int[]{ 11, infinity, infinity, infinity, 26, 0, 17, infinity, infinity },

new int[]{ infinity, 16, infinity, 24, infinity, 17, 0, 19, infinity },

new int[]{ infinity, infinity, infinity, 16, 7, infinity, 19, 0, infinity },

new int[]{ infinity, 12, 8, 21, infinity, infinity, infinity, infinity, 0 },

};

Prim(graph, numberOfVertexes);

//PrimSimplified(graph, numberOfVertexes);

}

static void Prim(int[][] graph, int numberOfVertexes)

{

bool debug = true;

int[] adjVex = new int[numberOfVertexes],  // 邻接顶点数组：搜索边的最小权值过程中各边的起点坐标

lowCost = new int[numberOfVertexes];   // 各边权值数组：搜索边的最小权值过程中各边的权值，数组下标为边的终点。

for (int i = 0; i < numberOfVertexes; i++) // 从图G的下标为0的顶点开始搜索。（也是图G的最小生成树的顶点集合）。

{

adjVex[0] = 0;

}

// 初始从下标为0的顶点开始到下标为i的顶点的边的权值去搜索。找lowCost中权值最小的下标i。

for (int i = 0; i < numberOfVertexes; i++)

{

lowCost[i] = graph[0][i];

}

int k = 0;                                 // 初始假定权值最小的边的终点的下标为k。

for (int i = 1; i < numberOfVertexes; i++)

{

if (debug)

{

Console.WriteLine($"Loop {i}");

Console.Write("lowCost: ");

PrintArray(lowCost);

Console.Write(" adjVex: ");

PrintArray(adjVex);

Console.WriteLine();

}

int minimumWeight = int.MaxValue;      // 搜索过程中发现到的最小的权值。初始设置为最大的整数值以示两点间无边。

for (int j = 1; j < numberOfVertexes; j++)

{

// lowCost中0表示该点已经搜索过了。lowCost[j] < minimumWeight即发现目前最小权值。

if (lowCost[j] != 0 && lowCost[j] < minimumWeight)

{

minimumWeight = lowCost[j];    // 发现目前最小权值。

k = j;                         // 目前最小权值的边的终点下标。

}

}

if (!debug)

{

Console.WriteLine($"({adjVex[k]}, {k})");  // 输出边

}

// 此时找到的k值即是权值最小的边的终点。将V[k]放入集合U。（这步可省略，因lowCost[j]已被标为“无需搜索”了）。

adjVex[i] = k;

// 0表示该点已经搜索过了，已不需要再被搜索了。

lowCost[k] = 0;

// 转到以V[k]为开始顶点的边，去与前面u为起始顶点到V[i]为终止顶点的边的权值去比较。

for (int j = 1; j < numberOfVertexes; j++)

{

// lowCost中0表示该点已经搜索过了。graph[k][j] < lowCost[j]即发现更小权值。

if (lowCost[j] != 0 && graph[k][j] < lowCost[j])

{

lowCost[j] = graph[k][j];  // 更新权值；索引j即终点下标。

adjVex[j] = k;             // 下次寻找权值小的边时，从k为下标的顶点为起点。

}

}

if (debug)

{

Console.Write("lowCost: ");

PrintArray(lowCost);

Console.Write(" adjVex: ");

PrintArray(adjVex);

Console.WriteLine();

}

}

}

static void PrimSimplified(int[][] graph, int numberOfVertexes)

{

int[] adjVex = new int[numberOfVertexes],  // 邻接顶点数组：搜索边的最小权值过程中各边的起点坐标

lowCost = new int[numberOfVertexes];   // 各边权值数组：搜索边的最小权值过程中各边的权值，数组下标为边的终点。

for (int i = 0; i < numberOfVertexes; i++)

{

adjVex[i] = 0;                         // 从图G的下标为0的顶点开始搜索。（也是图G的最小生成树的顶点集合）。

lowCost[i] = graph[0][i];              // 从下标为0的顶点开始到下标为i的顶点结束构成的边去搜索。找最小权值。

}

int k = 0;                                 // 初始假定权值最小的边的终点的下标为k。

for (int i = 1; i < numberOfVertexes; i++)

{

int minimumWeight = int.MaxValue;      // 搜索过程中发现到的最小的权值。初始设置为最大的整数值以示两点间无边。

for (int j = 1; j < numberOfVertexes; j++)

{

// lowCost中0表示该点已经搜索过了。lowCost[j] < minimumWeight即发现目前最小权值。

if (lowCost[j] != 0 && lowCost[j] < minimumWeight)

{

minimumWeight = lowCost[j];    // 发现目前最小权值。

k = j;                         // 目前最小权值的边的终点下标。

}

}

Console.WriteLine($"({adjVex[k]}, {k})");  // 输出边

lowCost[k] = 0;                        // 0表示该点已经搜索过了，已不需要再被搜索了。

// 转到以V[k]为开始顶点的边，去与前面u为起始顶点到V[i]为终止顶点的边的权值去比较。

for (int j = 1; j < numberOfVertexes; j++)

{

// lowCost中0表示该点已经搜索过了。graph[k][j] < lowCost[j]即发现更小权值。

if (lowCost[j] != 0 && graph[k][j] < lowCost[j])

{

lowCost[j] = graph[k][j];      // 更新权值；索引j即终点下标。

adjVex[j] = k;                 // 下次寻找权值小的边时，从k为下标的顶点为起点。

}

}

}

}

static void PrintArray(int[] array)

{

Console.Write("[ ");

for (int i = 0; i < array.Length - 1; i++) // 输出数组的前面n-1个

{

Console.Write($"{ToInfinity(array[i])}, ");

}

if (array.Length > 0)                      // 输出数组的最后1个

{

int n = array.Length - 1;

Console.Write($"{ToInfinity(array[n])}");

}

Console.WriteLine(" ]");

}

static string ToInfinity(int i) => i == int.MaxValue ? "∞" : i.ToString();

}

}

参考资料：

《大话数据结构》 - 程杰 著 - 清华大学出版社 第247页