Haar小波分析
一 尺度函数与小波函数
基本尺度函数定义为: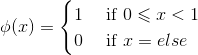 ,对其向右平移任意 k 个单位,构成函数族
,对其向右平移任意 k 个单位,构成函数族 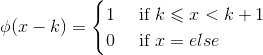 , 该函数族在
, 该函数族在 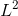 空间中正交,证明如下:
空间中正交,证明如下:
1 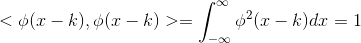 ;
;
2 当 m 不等于 k 时,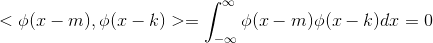
函数族 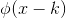 构成一组正交基,并形成
构成一组正交基,并形成 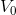 子空间。在
子空间。在 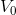 子空间中,任意函数均可表示为
子空间中,任意函数均可表示为  的线性组合,
的线性组合,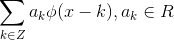 。
。
将函数族  构造宽度缩小一半,则可形成宽度为
构造宽度缩小一半,则可形成宽度为  的一组正交基,
的一组正交基,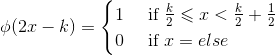 ,同样,该函数族在
,同样,该函数族在 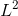 空间中正交,并形成
空间中正交,并形成 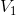 子空间。在
子空间。在 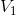 子空间中,任意函数均可表示为
子空间中,任意函数均可表示为 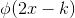 的线性组合,
的线性组合,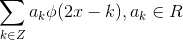 。
。
通过以上举例可得:设 j 为非负整数,j 级函数子空间可表示为 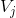 ,其对应正交基包括:
,其对应正交基包括:
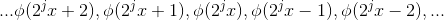 ,观察
,观察 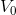 中
中 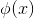 可有
可有 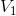 中
中  线性组合(
线性组合(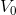 中任意函数均可用
中任意函数均可用 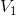 中函数线性组合表达),则
中函数线性组合表达),则 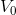 为
为 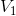 得子空间。各个子空间之间存在如下关系:
得子空间。各个子空间之间存在如下关系: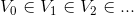 。
。
使用不同子空间 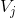 中尺度函数得线性组合,可以阶梯近似任意连续函数。在噪声滤除应用中,需要提取一些属于
中尺度函数得线性组合,可以阶梯近似任意连续函数。在噪声滤除应用中,需要提取一些属于 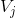 (高频信息)但不属于
(高频信息)但不属于 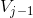 (低频信息)的方法,小波函数即描述了这部分信息,也即小波函数描述
(低频信息)的方法,小波函数即描述了这部分信息,也即小波函数描述  相对于
相对于 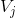 的正交补空间。根据以上描述,小波函数应该满足一些特性:
的正交补空间。根据以上描述,小波函数应该满足一些特性:
1 小波函数仍然位于 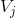 空间中,则他应该是
空间中,则他应该是 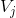 空间基函数的线性组合;
空间基函数的线性组合;
2 小波函数位于 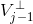 子空间中,则它应于
子空间中,则它应于 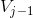 正交。
正交。
 空间的基本小波函数表示为:
空间的基本小波函数表示为: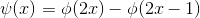 ,该函数位于
,该函数位于 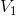 空间,且与
空间,且与 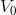 正交。同样对小波函数向右平移 k 个单位,构成函数族:
正交。同样对小波函数向右平移 k 个单位,构成函数族:
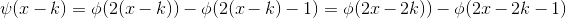 ,该函数族在
,该函数族在 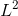 空间中正交。
空间中正交。
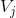 空间的基本小波函数表示为:
空间的基本小波函数表示为: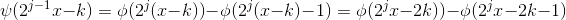 ,该函数族在
,该函数族在 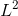 空间中正交。
空间中正交。
使用尺度函数与小波函数,可以将 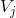 空间中函数进行分解:
空间中函数进行分解: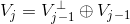 ,其中
,其中 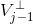 为
为 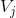 空间中的小波函数,继续以上分解,可得:
空间中的小波函数,继续以上分解,可得:
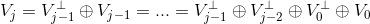
二 Haar分解
1 将函数离散化为 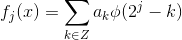 ,该函数位于
,该函数位于 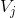 空间中;
空间中;
2 由于 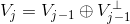 ,可以将
,可以将 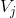 空间中该函数分解为
空间中该函数分解为 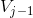 (更平滑尺度函数) 与
(更平滑尺度函数) 与 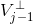 (小波函数),根据尺度函数与小波函数定义,有如下关系:
(小波函数),根据尺度函数与小波函数定义,有如下关系:
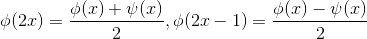 (根据图形可验证结论正确),进一步有:
(根据图形可验证结论正确),进一步有:
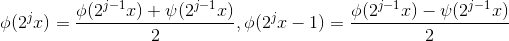 ;
;
3 观察到 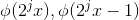 分解方式不一致,需要将原函数改写为:
分解方式不一致,需要将原函数改写为: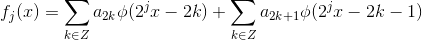 ;
;
4 对改写后的 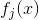 分别使用更平滑尺度函数与对应小波函数再次改写,有:
分别使用更平滑尺度函数与对应小波函数再次改写,有:
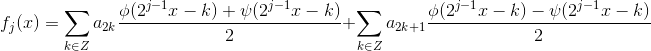 ,整理得:
,整理得:
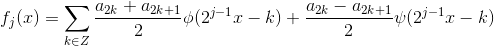 ;
;
5 令 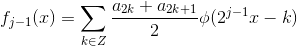 ,继续分解直到
,继续分解直到 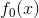 ,可得:
,可得:
 ,其中,
,其中,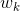 为相应的小波分量。
为相应的小波分量。
三 Haar重构
1 函数被分解为  , 其中,
, 其中,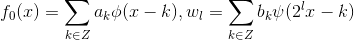 ;
;
2 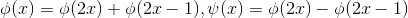 (根据图形可验证结论正确),进一步有:
(根据图形可验证结论正确),进一步有:
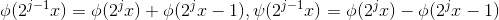
3 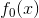 重构为
重构为 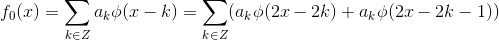 ;
;
4 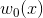 重构为
重构为 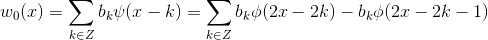 ;
;
5 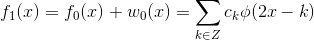 , 其中,
, 其中, 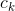 由
由 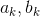 组合;
组合;
6 继续重构 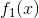 与
与  ,直到重构
,直到重构  。
。
参考资料 小波与傅里叶分析基础 Albert Boggess & Francis J. Narcowich
Haar小波分析的更多相关文章
- 图像算法五:【图像小波变换】多分辨率重构、Gabor滤波器、Haar小波
原 https://blog.csdn.net/alwaystry/article/details/52756051 图像算法五:[图像小波变换]多分辨率重构.Gabor滤波器.Haar小波 2018 ...
- Haar小波的理解
1. 首先理解L^2(R)的概念 L^2(R) 是一个内积空间的概念,表示两个无限长的向量做内积,张成的空间问题.也就是两个函数分别作为一个向量,这两个函数要是平方可积的.L^2(a,b)=<f ...
- 特征检测之Haar
Harr特征, 主要用于人脸检测,可以参考我的博文 基于MATLAB的adaboost级联形式的人脸检测实现 1 harr特征的原理 2 haar特征的计算 3 haar特征的应用
- 浅谈人脸检测之Haar分类器方法
我们要探讨的Haar分类器实际上是Boosting算法(提升算法)的一个应用,Haar分类器用到了Boosting算法中的AdaBoost算法,只是把AdaBoost算法训练出的强分类器进行了级联,并 ...
- OpenCv haar+SVM训练的xml检测人头位置
注意:opencv-2.4.10 #include "stdio.h"#include "string.h"#include "iostream&qu ...
- opencv - haar人脸特征的训练
step 1: 把正样品,负样品,opencv_createsamples,opencv_haartraining放到一个文件夹下面,利于后面的运行.step 2: 生成正负样品的描述文件 正样品描述 ...
- 图像特征提取三大法宝:HOG特征,LBP特征,Haar特征(转载)
(一)HOG特征 1.HOG特征: 方向梯度直方图(Histogram of Oriented Gradient, HOG)特征是一种在计算机视觉和图像处理中用来进行物体检测的特征描述子.它通过计算和 ...
- Haar特征
转自:http://blog.csdn.net/carson2005/article/details/8094699 Haar-like特征,即很多人常说的Haar特征,是计算机视觉领域一种常用的特征 ...
- 浅析人脸检测之Haar分类器方法
一.Haar分类器的前世今生 人脸检测属于计算机视觉的范畴,早期人们的主要研究方向是人脸识别,即根据人脸来识别人物的身份,后来在复杂背景下的人脸检测需求越来越大,人脸检测也逐渐作为一个单独的研究方向发 ...
随机推荐
- spring boot + spring security +JWT令牌 +前后端分离--- 心得
1.前言 观看这篇随笔需要有spring security基础. 心得: 1.生成token 的变化数据是用户名和权限拼接的字符串 ,其他的固定 2.生成的token是将登录通过的用户的权限拼接的字符 ...
- 还在用visio?这款画图工具才是真的绝!
最近有读者私信我,问我推文的配图是用什么工具画的,很好看,也想学习一下.今天就给大家介绍一下这款画图工具--Draw.io 概述 draw.io是一款免费的网页版画图工具(也有桌面版),支持流程图.U ...
- linux系统Kibana安装 汉化
Elasticsearch官方系列软件Kibana,在控制台管理维护Elasticsearch. 这里注意Elasticsearch和Kibana的版本一定要一致. 官网下载地址 https://ww ...
- 【pwn】DASCTF Sept 九月赛
[pwn]DASCTF Sept 月赛 1.hehepwn 先查看保护,栈可执行,想到shellcode 这题需要注意shellcode的写法 拖入ida中分析 一直以为iso scanf不能栈溢出, ...
- Qt之QFileDialog
widget.h: #ifndef WIDGET_H #define WIDGET_H #include <QWidget> #include<QString> class W ...
- 解决Post请求中文乱码问题
解决Post请求中文乱码问题 req.setChracterEncoding()要在获取请求参数前调用才有效,不然还是乱码
- 图文并茂理解iptables
原文地址:http://www.zsythink.net/archives/1199 以下是转载内容: iptables详解:图文并茂理解iptables | 朱双印博客 这篇文章会尽量以通俗易懂的方 ...
- dubbo-gateway 高性能dubbo网关
dubbo-gateway dubbo-gateway 提供了http协议到dubbo协议的转换,但[并非]使用dubbo的[泛化]调用(泛化调用性能比普通调用有10-20%的损耗,通过普通异步的调用 ...
- python 小兵面向对象
Python 面向对象 Python从设计之初就已经是一门面向对象的语言,正因为如此,在Python中创建一个类和对象是很容易的.本章节我们将详细介绍Python的面向对象编程. 如果你以前没有接触过 ...
- ApacheCN 深度学习译文集 20210112 更新
新增了六个教程: TensorFlow 2 和 Keras 高级深度学习 零.前言 一.使用 Keras 入门高级深度学习 二.深度神经网络 三.自编码器 四.生成对抗网络(GAN) 五.改进的 GA ...
