OO_Unit1_表达式求导
一、第一次作业
1.需求分析
简单多项式导函数
- 带符号整数 支持前导0的带符号整数,符号可省略,如:
+02、-16、19260817等。 - 幂函数
- 一般形式 由自变量x和指数组成,指数为一个带符号整数,如:
x ^ +2。 - 省略形式 当指数为1的时候,可以采用省略形式,如:
x。
- 一般形式 由自变量x和指数组成,指数为一个带符号整数,如:
- 项
- 变量项
- 带有系数的幂函数,如:
2 * x ^ 2、-1 * x。 - 系数为1的时候,可以省略系数或表示为正号开头的形式,如:
x ^ 2、+ x ^ 2。 - 系数为-1的时候,可以表示为负号开头的形式,如:
-x ^ 2。
- 带有系数的幂函数,如:
- 常数项 包含一个带符号整数,如:
233。
- 变量项
- 表达式 由加法和减法运算符连接若干项组成,如:
-1 + x ^ 233 - x ^ 06。此外,在第一项之前,可以带一个正号或者负号,如:- -1 + x ^ 233、+ -2 + x ^ 19260817。注意,空串不属于合法的表达式。 - 空白字符 在本次作业中,空白字符包含且仅包含
<space>和\t。
2.实现方案
输入合法判断 使用java中自带的正则表达式匹配
java.util.regex.Matcher和java.until.regx.Pattern进行输入的匹配。由于第一次作业字符串长度不限制长度,不能一次匹配完整个表达式(否则会出现正则爆栈),故使用了itemFitem分别匹配第一项和后面的项:String num = "([+-]?0*[0-9]+)";
String pow = "(\\s*x\\s*" + "(\\^\\s*" + num + ")?)";
String variableWith = "(\\s*" + num + "\\s*\\*" + pow + ")";
String variableWithout = "(\\s*[+-]?\\s*" + pow + ")";
String variable = "(" + variableWith + "|" + variableWithout + ")";
String constant = "(\\s*" + num + ")";
String itemF = "(\\s*[+-]?" + "(" + variable + "|" + constant + "))";
String item = "(\\s*[+-]" + "(" + variable + "|" + constant + "))";
String polyStyle = "^" + itemF + item + "*\\s*$";//结尾也可能有空格
此处最好将
\\s改成[\\t ]以避免\\v\\f等不合法输入出现输入预处理 只需要将空格删除即可
s = s.replaceAll("\\s", "");建立类图 第一次作业较为简单,没有多考虑,只建立了一个Item类,是(coef,exp)的二元组,在主控类Derivative中使用了一个静态数组
Item[] poly:用来存入Item(类图省略)实现思路 每匹配到一项,便将其作为Item构造器的输入,全部构造完成后,对poly进行选择排序,并且从尾到头遍历一遍,合并指数相同的项(前面的coef设为0,后面的coef等于两者之和)
3.测试及修复
- 测试思路 此次作业相对简单,测试的思路也并不复杂,只需要按照指导书对每一种不同的省略输入进行测试即可
- bug修复 本次作业由于未进行极端数据测试以及输出格式测试,出现了2个bug
- BigInteger 最开始使用的是
int,以至于一旦碰到较大的数据都会数据异常,例如:100000000*x^1111111111111 - 输出
*x在系数是+1或-1的情况下省略了1,却没考虑不输出*,表达式中出现了+*x,输出格式错误 - 没有将正项提前 由于实验希望我们输出最小长度的项,提前正项使长度减1
- BigInteger 最开始使用的是
二、第二次作业
1.需求分析
在第一次作业基础上,加入了因子以及三角函数
- 带符号整数
- 因子
- 变量因子
- 幂函数
- 一般形式
- 省略形式
- 三角函数
sin(x)或cos(x)(在本次作业中,括号内仅为x)- 一般形式 类似于幂函数,由
sin(x)和指数组成,指数为一个带符号整数,如:sin(x) ^ +2。 - 省略形式 当指数为1的时候,可以采用省略形式,省略指数部分,如:
sin(x)。
- 一般形式 类似于幂函数,由
- 幂函数
- 常数因子
- 变量因子
- 项
- 一般形式 由乘法运算符连接若干因子组成,如:
2 * x ^ 2 * 3 * x ^ -2、sin(x) * cos(x) * x。 - 特殊情况
- 第一个因子为常数因子,且值为1
- 第一个因子为常数因子,且值为-1
- 一般形式 由乘法运算符连接若干因子组成,如:
- 表达式
- 空白字符
2.实现方案
输入合法判断 类似第一次,增添了三角的形式
private static String space = "[\\t ]*";
private static String signedNum = "(" + space + "[+-]?0*[0-9]+)";
private static String power = "(" + space + "x" + space
+ "(\\^" + signedNum + ")?)";
private static String triang = "(" + space + "(sin|cos)" + space + "\\("
+ space + "x" + space + "\\)" + space + "(\\^" + signedNum + ")?)";
private static String factor = "(" + signedNum +
"|" + power + "|" + triang + ")"; //每一项前可能有+-作为 +1* -1*的缩写
private static String item = "(" + space + "[+-]?" + factor
+ "(" + space + "\\*" + factor + ")*)";
private static String itemF = "(" + space + "[+-]?" + item + ")";
private static String itemNF = "(" + space + "[+-]" + item + ")"; private static String poly = "^" + itemF + itemNF + "*" + space + "$";
空文件报错 第一次忽略一种情况,直接使用
s = sc.nextLine();会出现无输入异常,需要判断是否为空:Scanner sc = new Scanner(System.in);
if (!sc.hasNext()) {
System.out.println("WRONG FORMAT!");
sc.close();
System.exit(0);
} String s = sc.nextLine();
输入预处理 同第一次,
s = s.replaceAll(space, "");建立类图 建立了
PolyItemSubPoly类,分别用来存表达式,项,和指数相同的序列(用来化简):
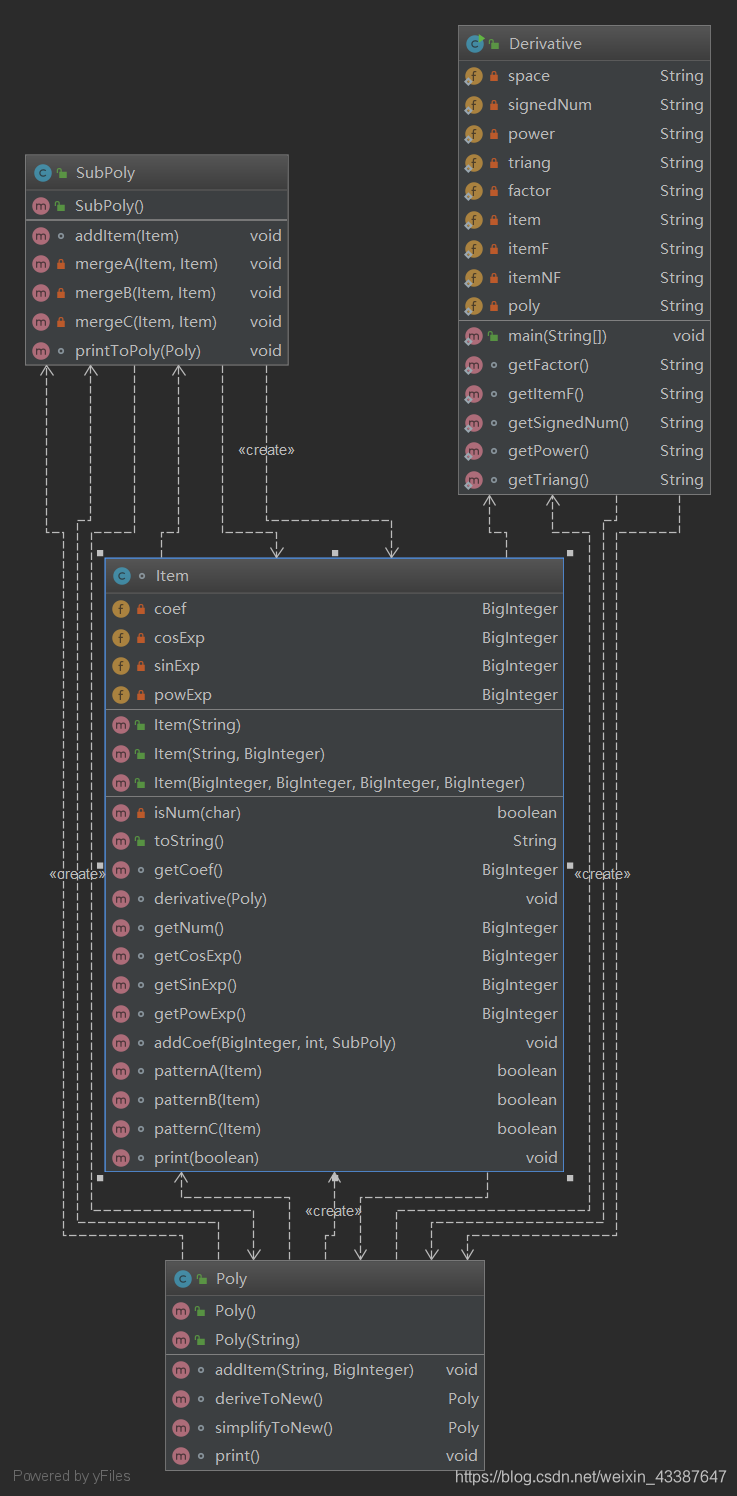
如图,Poly类是HashMap的子类,而SubPoly是ArrayList的子类。主控类
Derivative只和Poly类有依赖关系,剩下的事情交给三个类之间交互。实现思路 整个字符串作为Poly的构造器传入,将匹配到的每一项作为Item的传入,构造完成后,一次次分离出Poly的子序列SubPoly并化简,输出到一个新的Poly中,最后将新的Poly输出
Poly poly = new Poly(s);
poly = poly.simplifyToNew();
poly = poly.deriveToNew();
poly = poly.simplifyToNew();
poly.print();
3.测试及修复
- 结构分析
- 复杂度分析(只显示超标)

- 依赖关系分析
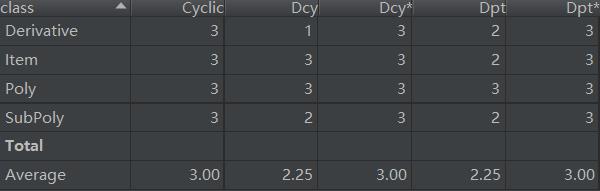
- 复杂度分析(只显示超标)
- 测试思路 本次使用了自动化测试:
打包成.jar->按正则create输入->命令行输入到.jar并输出到文件->分析比对结果(可以使用自带的symplify看结果是否为0)以下是用python语言写的自动化代码:import os
from xeger import Xeger names = ["derivative", "Assassin", "Caster", "Lancer", "Archer", "Rider", "Saber", "Alterego"] def run():
for name in names:
os.system('java -jar jar/' + name + '.jar< in.txt' + ' > ' + name + '.txt') def out():
l = []
for name in names:
f = open(name + '.txt', "r")
s = f.read()
s = s.translate(str.maketrans('', '', '\n'))
print(name + ':\t', len(s))
# print(s)
if s == "WRONG FORMAT!":
print(s)
l.append(1000000000000)
else:
l.append(len(s))
return l def create():
testStr = Xeger(limit=2).xeger(poly)
return testStr def putToIn(s):
fh = open("in.txt", 'w', encoding='utf-8')
fh.write(s)
fh.close() for i in range(20):
s = create()
print(s)
putToIn(s)
run()
l = out()
- bug修复
三、第三次作业
1.需求分析
在第二次作业的基础上,加入了嵌套,并且表达式也能作为因子
- 带符号整数
- 因子
- 变量因子
- 幂函数
- 三角函数
sin(x),cos(x)
- 常数因子
- 表达式因子 将在表达式的相关设定中进行详细介绍。不过,表达式因子不支持幂运算。
- 嵌套因子 本次作业将支持因子嵌套在三角函数因子里面,即一个因子作为另一个三角函数因子的自变量,例如
sin(x^2),cos(sin(x))以及sin(sin(cos(cos(x^2))))^2等。但是不允许出现指数为变量的情况,指数依然只能是带符号整数。也不允许幂函数的自变量为除了x之外的因子。
- 变量因子
- 项
- 一般形式
- 项内因子不仅仅是同类因子
- 特殊形式
- 一般形式
- 表达式 由加法和减法运算符等若干项组成
- 表达式因子 表达式可以作为因子,其定义为被一对小括号包裹起来的表达式,即我们允许诸如
(x * cos(x))这种式子的出现 - 空串不属于合法的表达式
- 表达式因子 表达式可以作为因子,其定义为被一对小括号包裹起来的表达式,即我们允许诸如
- 空白字符
2.实现方案
输入合法判断 这一次作业不存在一个统一的字符串去匹配整个输入。因为输入中含有嵌套,必须在一步步分解中逐渐递归拆解,然后在子的递归中继续判断表达式是否合法。因此,很容易出错。
输入预处理 同前两次相比复杂了不少。由于在递归中很难完成对符号正确性(例如
+++1+ + sin(x)- -x +++1)的判断。所以必须在构造表达式之前先把接连出现符号(指[+-])的情况处理掉。对此的处理也比较复杂://先判断字符串中是否存在:①连用四个符号②连用三个符号且第三个符号不与数字相连
//③在*后面连用两个符号④在*号后面用了一个符号且不与数字相连
if (!examsymbol(s)) {
System.out.print("WRONG FORMAT!");
System.exit(0);
} //将所有多符号的地方(两个或三个)全部替换为单一符号
s = strip(s); //将所有非常数项(不是符号紧跟数字的)中出现的-号替换为(-1)*
int i = 0;
while (s.substring(i).contains("-")) {
i = s.indexOf("-") + 1;
if (!isnum(s.charAt(i))) {
s = s.replace("-", "+(-1)*");
}
}
建立类图 本次表达式较为复杂,按照老师的提示,我自己也画出了一个大致的类图:
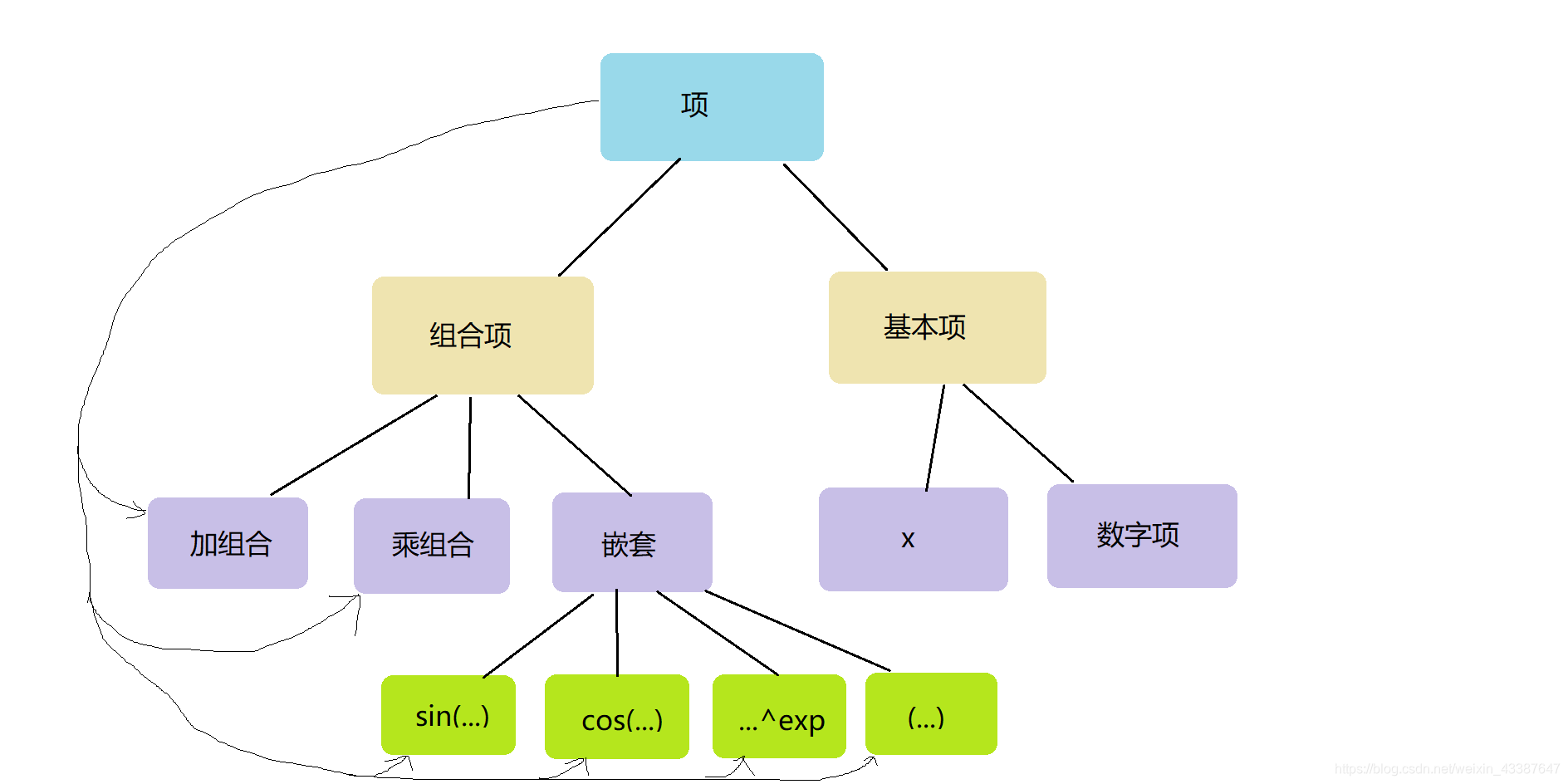
如图所示:上下级之间为泛化关系,项有是
加组合项,乘组合项,及各个嵌套项的组合关系。主控类直接与项依赖,而与其他的类都没有耦合关系,最后代码中的类图(略去除泛化以外的耦合关系)如下: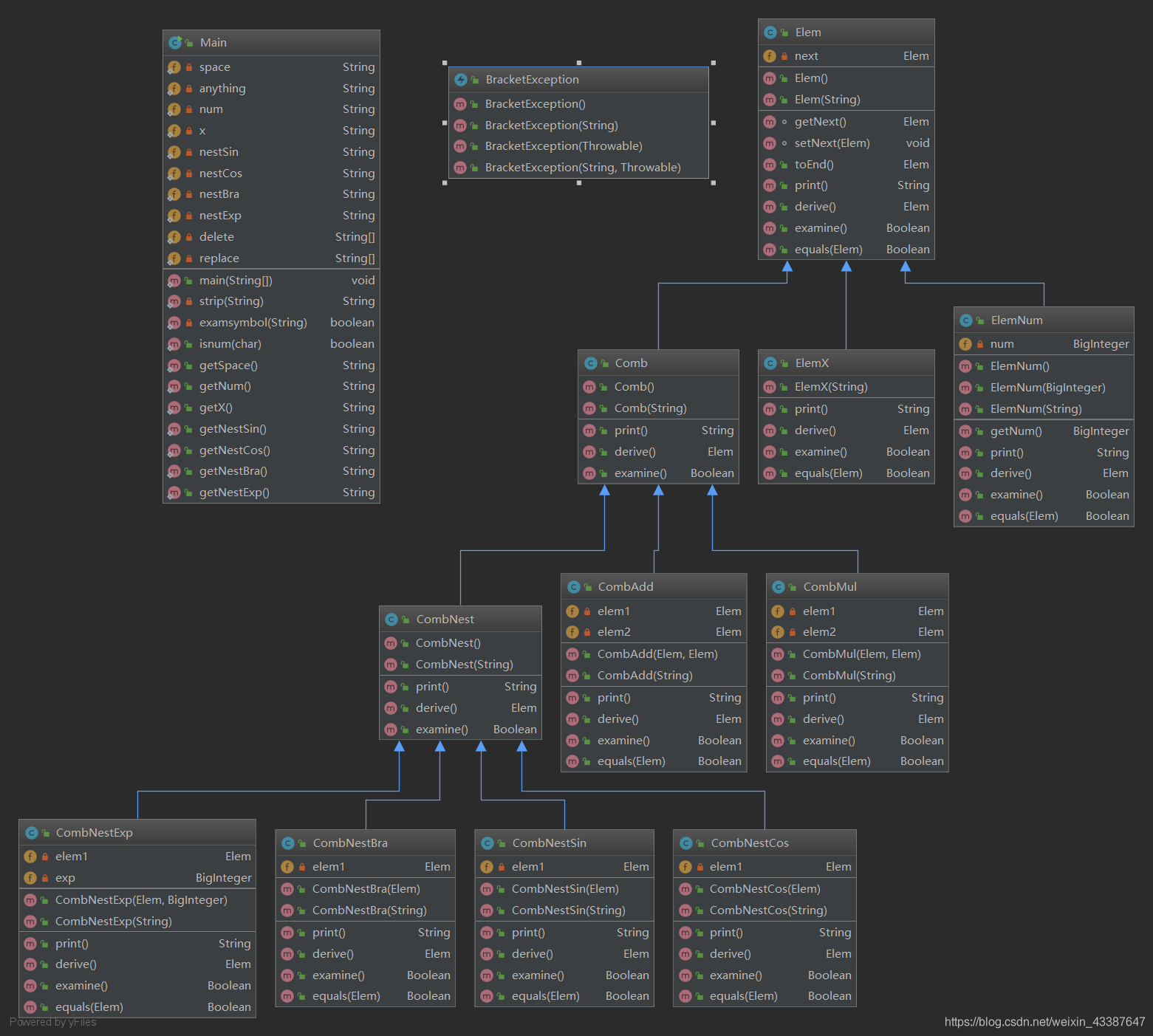
实现思路
实现的难点一 在于如何通过向构造器传递一个字符串s,而创建一个叶子类的对象(即最底层的,没有子类的类)。目前想到的办法是在非叶子类中加入一个指向根类对象的引用
next,让父类尝试各种子类的构造方法,成功了就让next指向该对象,如果都不成功则抛出异常。private Elem next; public Elem() { } public Elem(String s) {
try {
next = new Comb(s).toEnd();
} catch (IllegalArgumentException e1) {
try {
next = new ElemNum(s);
} catch (IllegalArgumentException e2) {
try {
next = new ElemX(s);
} catch (IllegalArgumentException e3) {
throw new IllegalArgumentException("Not Elem");
}
}
}
}
例如在Elem类中:除了默认的构造方法外,依次尝试所有子类的构造方法,并将
next指向他,对于非叶节点的对象,总在其后加上toEnd()方法:public Elem toEnd() {
Elem elem = this;
while (elem.next != null) {
elem = elem.next;
}
return elem;
}
实现的难点二 在于如何判断格式是否正确,格式的问题在构造时已经由相应的构造方法解决。但幂函数的底数不能是加组合和乘组合需要自己新定义一个方法去检查是否自己是表达式因子,在不同子类中重写不同。
其中:括号嵌套,加组合,乘组合,返回的是true,而密函数嵌套类只要他的底数的examine返回值是true则抛出异常。
public Boolean examine() throws BracketException {
elem1.examine();
return true;
}
3.测试及修复
- 结构分析
复杂度分析(只显示超标的)
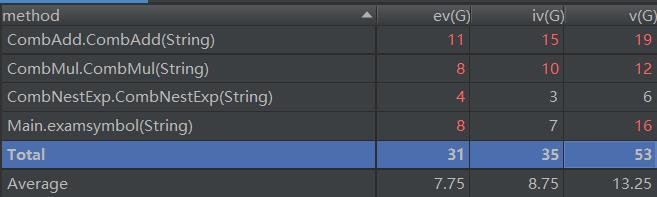
可以看出,不少类(加组合、乘组合、幂函数嵌套)的构造方法基本复杂度很高。这也是因为我传入构造器中的是字符串,分析处理字符串对于构造器来说任务量太大。按照助教的方法,应该写以下几个类:
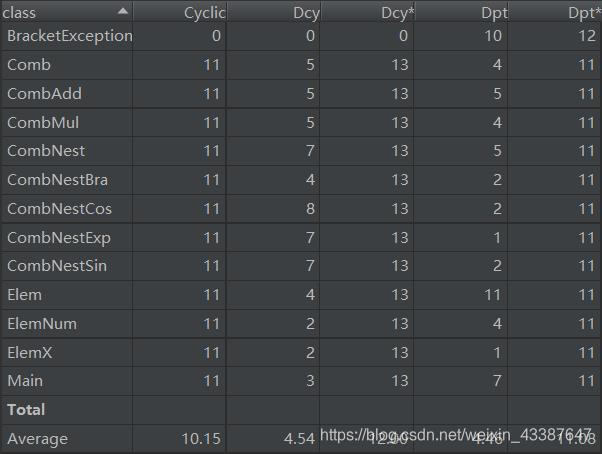
FactorParserPolyParserItemParser,分析完字符串后直接传入这些类的构造器。依赖关系分析
- 测试思路 本次作业几乎要兼容第二次作业里的绝大部分,只需要将exp这一字符串所表示的正则表达式的指数改为
(0,10000)的整数即可。 - bug修复 本次作业bug也相当多,大多是关于格式的错误,还有嵌套层数过深,出现了
StackOverFlowError以及CPU_TIME_LIMIT_EXCEED错误,列举如下:bug1:
sin(-9)因为最开始将所有-替换为+(-1)*,使得在sin()嵌套中的-9被误诊断为乘组合项,而输出WF.修正 ①将替换算法修改非常数项,②在判断加组合项中取消只要碰到括号外的符号即生成,如
+9不再判断为0+9。bug2: 没有识别出
*+x的WF错误.修正 在预处理时判断是否读到*号,在此后如果出现了不带数字的符号即判断为WF
bug3: 判断
sin((x+1))^2为WF,以为幂函数的底数只要出现了因子即判断为WF修正 仅当幂底为加组合、乘组合、括号嵌套时判断为WF
bug4: 如
8* -008- - 017 * 07* x +- 091 * sin ( x ) * cos( x)当嵌套层数比较深时,出现StackOverFlowError修正 减少嵌套层数,加组合和乘组合不再定义为二叉树,而是多叉树
bug5: 如
sin((x+cos((sin((x^2-cos(x)^3+sin(x)^4))+cos((sin(x)-x)))))),当嵌套层数比较深时,出现CPU_TIME_LIMIT_EXCEED修正 减少嵌套层数,加组合和乘组合不再定义为二叉树,而是多叉树
四、三次作业总结
三次作业由浅入深,无论是难度、思考量、代码量、还是花在题目上的时间都呈几何倍数递增。但是在做题的过程中收获得更多,思想境界从原本的面向过程逐渐深入了解面向对象的精髓。
为了准备研讨课,在网上查阅了大量资料,对面向对象是什么有了深入了解,最后附上研讨课上讨论使用的ppt:

OO_Unit1_表达式求导的更多相关文章
- OO_Unit1_表达式求导总结
OO_Unit1_表达式求导总结 OO的第一单元主要是围绕表达式求导这一问题布置了3个子任务,并在程序的鲁棒性与模型的复杂度上逐渐升级,从而帮助我们更好地提升面向对象的编程能力.事实也证明,通过这 ...
- OO Unit 1 表达式求导
OO Unit 1 表达式求导 面向对象学习小结 前言 本博主要内容目录: 基于度量来分析⾃己的程序结构 缺点反思 重构想法 关于BUG 自己程序出现过的BUG 分析⾃己发现别人程序bug所采⽤的策略 ...
- BUAA-OO-第一单元表达式求导作业总结
figure:first-child { margin-top: -20px; } #write ol, #write ul { position: relative; } img { max-wid ...
- 2019年北航OO第1单元(表达式求导)总结
2019年北航OO第1单元(表达式求导)总结 1 基于度量的程序结构分析 量化指标及分析 以下是三次作业的量化指标统计: 关于图中指标在这里简要介绍一下: ev(G):基本复杂度,用来衡量程序非结构化 ...
- 2020 OO 第一单元总结 表达式求导
title: BUAA-OO 第一单元总结 date: 2020-03-19 20:53:41 tags: OO categories: 学习 OO第一单元通过三次递进式的作业让我们实现表达式求导,在 ...
- 面向对象第一单元总结:Java实现表达式求导
面向对象第一单元总结:Java实现表达式求导 题目要求 输入一个表达式:包含x,x**2,sin(),cos(),等形式,对x求导并输出结果 例:\(x+x**2+-2*x**2*(sin(x**2+ ...
- oo第一次博客-三次表达式求导的总结与反思
一.问题回顾与基本设计思路 三次作业依次是多项式表达式求导,多项式.三角函数混合求导,基于三角函数和多项式的嵌套表达式求导. 第一次作业想法很简单,根据指导书,我们可以发现表达式是由各个项与项之间的运 ...
- OO_JAVA_表达式求导_单元总结
OO_JAVA_表达式求导_单元总结 这里引用个链接,是我写的另一份博客,讲的是设计层面的问题,下面主要是对自己代码的单元总结. 程序分析 (1)基于度量来分析自己的程序结构 第一次作业 程序结构大致 ...
- OO_JAVA_表达式求导
OO_JAVA_表达式求导_第一弹 ---------------------------------------------------表达式提取部分 词法分析 首先,每一个表达式内部都存在不可 ...
随机推荐
- IDA报错fatal error before kernel init
编写了一个IDA64插件,结果再打开IDA后报错fatal error before kernel init,然后闪退. 检查了一遍代码没发现有问题,后来发现是环境有一处配置错误, IDA64.exe ...
- 使用C# (.NET Core) 实现模板方法模式 (Template Method Pattern)
本文的概念内容来自深入浅出设计模式一书. 项目需求 有一家咖啡店, 供应咖啡和茶, 它们的工序如下: 咖啡: 茶: 可以看到咖啡和茶的制作工序是差不多的, 都是有4步, 其中有两步它们两个是一样的, ...
- 【odoo14】第二十三章、管理邮件
邮件集成是odoo最重要的特性.我们可以通过odoo收发邮件.我们甚至可以管理业务文档上的电子邮件,如潜在客户.销售订单和项目.本章,我们将探讨在odoo中处理邮件的方式. 配置邮件服务器 管理文档中 ...
- python中zip函数的使用
zip(*iterables) zip可以将多个可迭代对象组合成一个迭代器对象,通过迭代取值,可以得到n个长度为m的元组.其中n为长度最短可迭代对象的元素个数,m为可迭代对象的个数.并且每个元组的第i ...
- ON DUPLICATE KEY UPDATE作用
ON DUPLICATE KEY UPDATE作用 先声明一点,ON DUPLICATE KEY UPDATE为Mysql特有语法,这是个坑 语句的作用,当insert已经存在的记录时,执行Updat ...
- 201871010130-周学铭 实验二 个人项目—D{0-1}问题项目报告
项目 内容 课程班级博客链接 18级卓越班 这个作业要求链接 实验二 软件工程个人项目 我的课程学习目标 掌握软件项目个人开发流程.掌握Github发布软件项目的操作方法. 这个作业在哪些方面帮助我实 ...
- Semaphore自白:限流器用我就对了!
大家好,我是 Semaphore,我的中文名字叫"信号量",我来自 JUC(java.util.concurrent)家族. 我们家族有很多优秀的成员,比如:CountDownLa ...
- 解决SQLPLUS无法使用上下箭头
1 问题描述 SQLPLUS中使用上下箭头无法获取历史命令,如下图所示: 按上下箭头会显示^[[A/^[[B. 2 解决方案 需要安装rlwrap,可以的话可以用包管理器安装,笔者环境CentOS,这 ...
- redhat7.6 更换 centos7 YUM
使用yum 遇到如下错误. This system is not registered to Red Hat Subscription Management. You can use subscrip ...
- poi 操作 PPT,针对 PPTX--图表篇
poi 操作 PPT,针对 PPTX--图表篇 目录 poi 操作 PPT,针对 PPTX--图表篇 1.读取 PPT 模板 2.替换标题 4.替换图表数据 接下来对 ppt 内的图表进行操作,替换图 ...
