机器学习--支持向量机 （SVM）算法的原理及优缺点

一、支持向量机 （SVM）算法的原理

　　支持向量机（Support Vector Machine，常简称为SVM）是一种监督式学习的方法，可广泛地应用于统计分类以及回归分析。它是将向量映射到一个更高维的空间里，在这个空间里建立有一个最大间隔超平面。在分开数据的超平面的两边建有两个互相平行的超平面，分隔超平面使两个平行超平面的距离最大化。假定平行超平面间的距离或差距越大，分类器的总误差越小。

　　1.支持向量机的基本思想

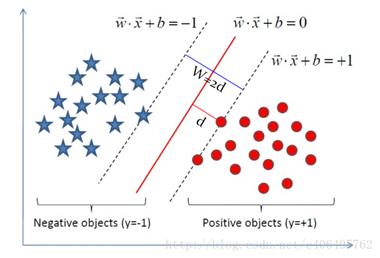
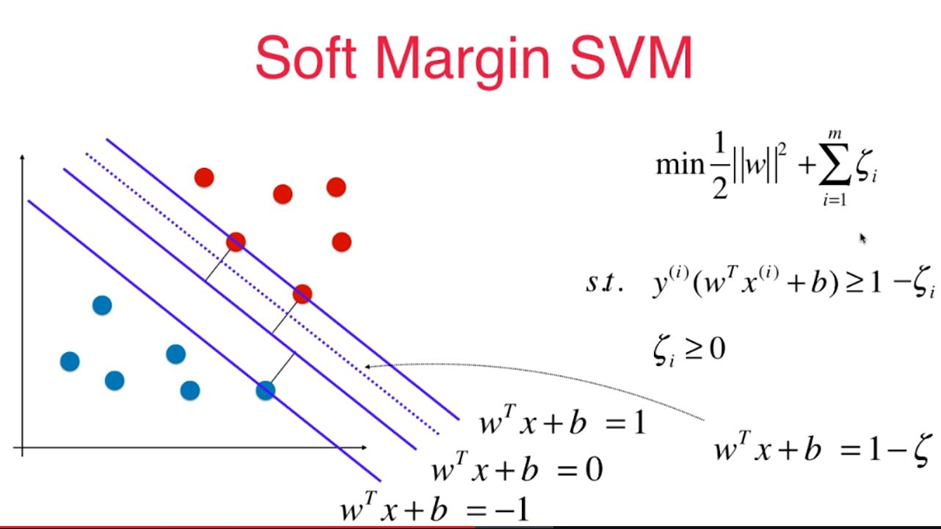
　　对于线性可分的任务，找到一个具有最大间隔超平面，如图所示，

　　                            

　　（1）支持向量机的基本型为：

                                 

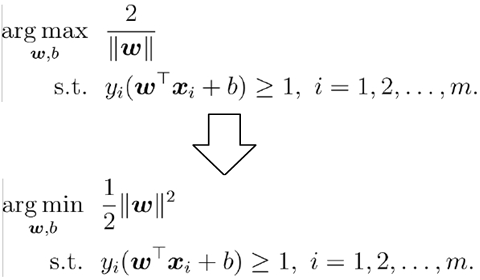
　　（2）软间隔的优化目标：

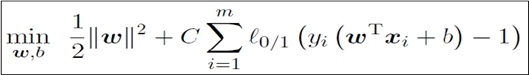
　　　　　　其中，0-1函数为错分样本的个数。

　　（3）核方法：

　　　　                 

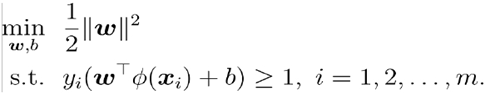
　　　　　　其中为特征映射函数。

　　2、实验一般步骤：

　　 （1）导入数据；

　　（2）数据归一化；

　　（3）执行svm寻找最优的超平面；

　　（4）绘制分类超平面核支持向量；

　　（5）利用多项式特征在高维空间中执行线性svm

　　（6）选择合适的核函数，执行非线性svm；

　　3、算法优缺点：

　　　　算法优点：　　

　　　　（1）使用核函数可以向高维空间进行映射

　　　　（2）使用核函数可以解决非线性的分类

　　　　（3）分类思想很简单，就是将样本与决策面的间隔最大化

　　　　（4）分类效果较好

　　　　算法缺点：

　　　　（1）SVM算法对大规模训练样本难以实施

　　　　（2）用SVM解决多分类问题存在困难

　　　　（3）对缺失数据敏感，对参数和核函数的选择敏感　　

二、数学推导过程

　　

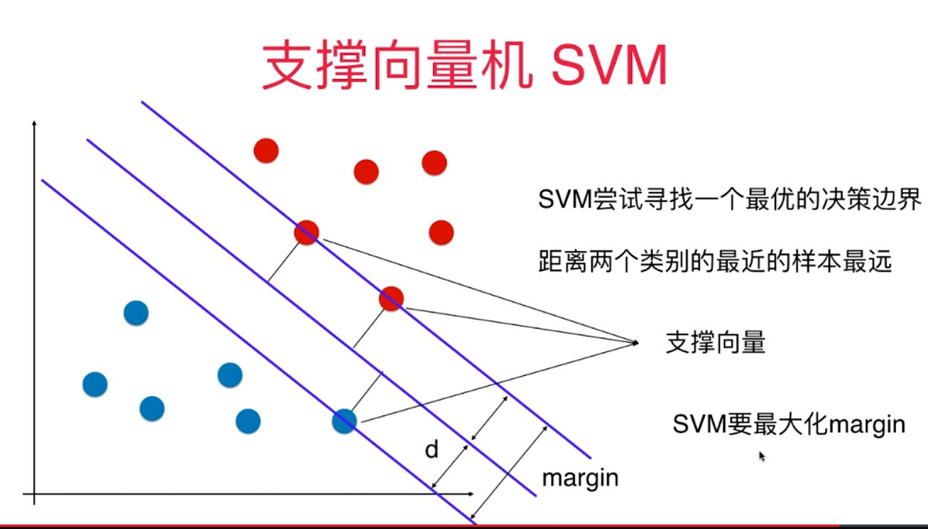
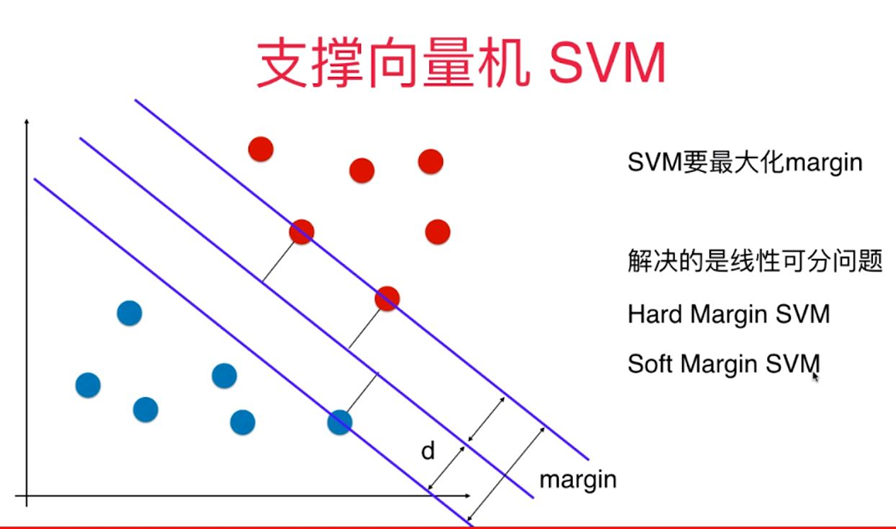
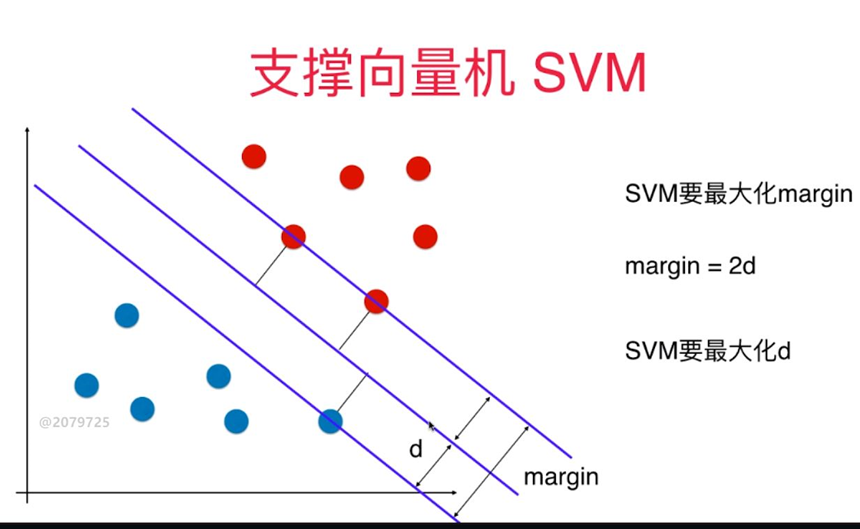
　　对于线性可分的支持向量机求解问题实际上可转化为一个带约束条件的最优化求解问题：

　　　　推理过程：

　　　　　　    

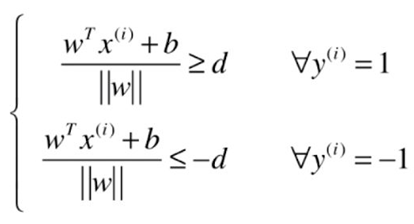
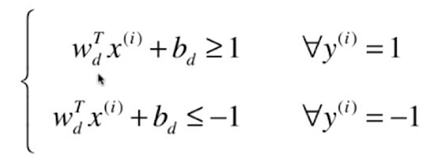
　　　　　　　　　　　　　　　　　结果：

　　　　                                                   

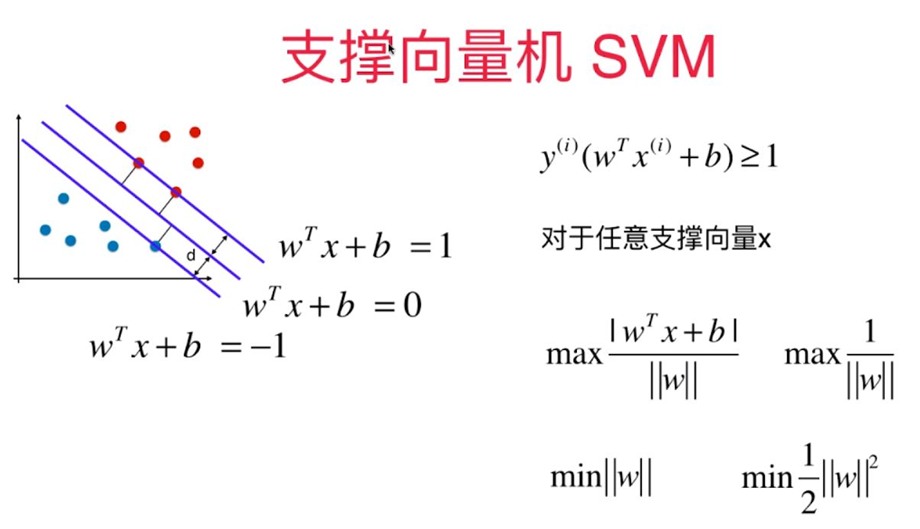
　　对于线性不可分的支持向量机求解问题实际上可转化为一个带约束条件的soft-margin最优化求解问题：

　　　　                         

　　

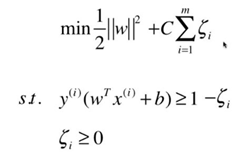
三、代码实现

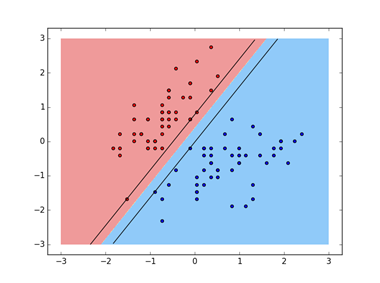
1、线性svm

import numpy as np
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
from matplotlib.colors import ListedColormap
import warnings

def plot_decision_boundary(model,axis):
    x0,x1=np.meshgrid(
        np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)).reshape(-1,1),
        np.linspace(axis[2],axis[3],int((axis[3]-axis[2])*100)).reshape(-1,1)
    )
    x_new=np.c_[x0.ravel(),x1.ravel()]
    y_predict=model.predict(x_new)
    zz=y_predict.reshape(x0.shape)
    custom_cmap=ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    plt.contourf(x0,x1,zz,linewidth=5,cmap=custom_cmap)

    w = model.coef_[0]
    b = model.intercept_[0]
    plot_x = np.linspace(axis[0],axis[1],200)
    up_y = -w[0]/w[1]*plot_x - b/w[1] + 1/w[1]
    down_y = -w[0]/w[1]*plot_x - b/w[1] - 1/w[1]
    up_index = (up_y>=axis[2]) & (up_y<=axis[3])
    down_index = (down_y>=axis[2]) & (down_y<=axis[3])
    plt.plot(plot_x[up_index],up_y[up_index],c='black')
    plt.plot(plot_x[down_index],down_y[down_index],c='black')
warnings.filterwarnings("ignore")
data = load_iris()
x = data.data
y = data.target
x = x[y<2,:2]
y = y[y<2]

scaler = StandardScaler()
scaler.fit(x)
x = scaler.transform(x)
svc = LinearSVC(C=1e9)
svc.fit(x,y)

plot_decision_boundary(svc,axis=[-3,3,-3,3])
plt.scatter(x[y==0,0],x[y==0,1],c='r')
plt.scatter(x[y==1,0],x[y==1,1],c='b')
plt.show()

输出结果：

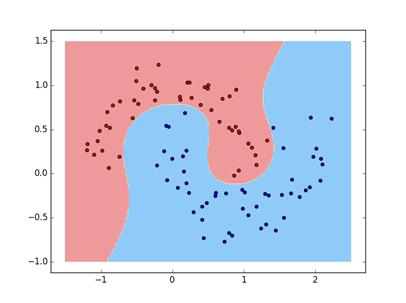
 2、非线性-多项式特征

import numpy as np
from sklearn import datasets
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures,StandardScaler
from sklearn.svm import LinearSVC
from sklearn.pipeline import Pipeline
from matplotlib.colors import ListedColormap
import warnings

def plot_decision_boundary(model,axis):
    x0,x1=np.meshgrid(
        np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)).reshape(-1,1),
        np.linspace(axis[2],axis[3],int((axis[3]-axis[2])*100)).reshape(-1,1)
    )
    x_new=np.c_[x0.ravel(),x1.ravel()]
    y_predict=model.predict(x_new)
    zz=y_predict.reshape(x0.shape)
    custom_cmap=ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    plt.contourf(x0,x1,zz,linewidth=5,cmap=custom_cmap)

def PolynomialSVC(degree,C=1.0):
    return Pipeline([
        ('poly',PolynomialFeatures(degree=degree)),
        ('std_scaler',StandardScaler()),
        ('linearSVC',LinearSVC(C=1e9))
    ])

warnings.filterwarnings("ignore")
poly_svc = PolynomialSVC(degree=3)
X,y = datasets.make_moons(noise=0.15,random_state=666)
poly_svc.fit(X,y)
plot_decision_boundary(poly_svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1],c='red')
plt.scatter(X[y==1,0],X[y==1,1],c='blue')
plt.show()

输出结果：

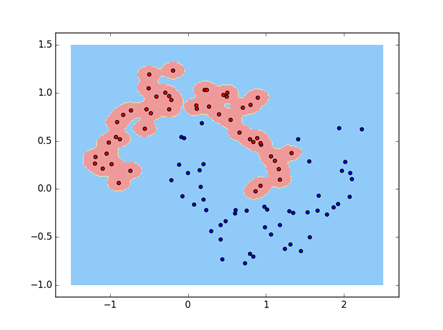
3、非线性-核方法

from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.pipeline import Pipeline
from sklearn import datasets
from matplotlib.colors import ListedColormap
import numpy as np
import matplotlib.pyplot as plt
import warnings
def plot_decision_boundary(model,axis):
    x0,x1=np.meshgrid(
        np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)).reshape(-1,1),
        np.linspace(axis[2],axis[3],int((axis[3]-axis[2])*100)).reshape(-1,1)
    )
    x_new=np.c_[x0.ravel(),x1.ravel()]
    y_predict=model.predict(x_new)
    zz=y_predict.reshape(x0.shape)
    custom_cmap=ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    plt.contourf(x0,x1,zz,linewidth=5,cmap=custom_cmap)
def RBFKernelSVC(gamma=1.0):
    return Pipeline([
        ('std_scaler',StandardScaler()),
        ('svc',SVC(kernel='rbf',gamma=gamma))
    ])
warnings.filterwarnings("ignore")
X,y = datasets.make_moons(noise=0.15,random_state=666)
svc = RBFKernelSVC(gamma=100)
svc.fit(X,y)
plot_decision_boundary(svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1],c='red')
plt.scatter(X[y==1,0],X[y==1,1],c='blue')
plt.show()

输出结果：