三维动画形变算法（Gradient-Based Deformation）

　　将三角网格上的顶点坐标（x，y，z）看作3个独立的标量场，那么网格上每个三角片都存在3个独立的梯度场。该梯度场是网格的微分属性，相当于网格的特征，在形变过程中随控制点集的移动而变化。那么当用户拖拽网格上的控制点集时，网格形变问题即变为求解以下式子：

　　根据变分法，上式最小化即求解泊松方程：

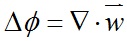
其中Φ为待求的网格形变后坐标，w为网格形变后的梯度场。

　　上式可以进一步表示为求解稀疏线性方程组：

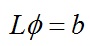
其中L为网格的拉普拉斯算子，b为梯度场w在网格顶点处的散度值。

　　问题的关键是如何得到网格形变后的梯度场w，文章[Yu et al. 2004]提到其是通过由控制点集变换的加权运算得到，并且提出了几种不同的加权方式（线性加权，高斯加权等）。另外文章[Zayer et al. 2005]中提到可以在网格内构建一个调和场作为加权系数。

1.离散梯度算子定义：

      假设f是一个分片线性函数，在网格的每个三角片{x_i，x_j，x_k}的顶点处有f(x_i)=f_i，f(x_j)=f_j，f(x_k)=f_k，通过线性插值可以知道f在三角片上每一点处的值为：

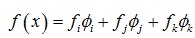
　　这样f的梯度如下：

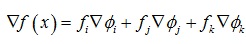
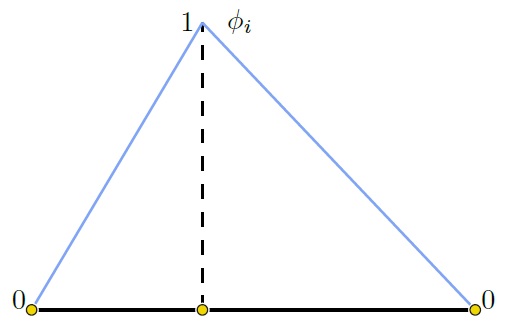
其中基函数Φ_i，Φ_j，Φ_k满足Φ_i+Φ_j+Φ_k=1，那么它们梯度之和▽Φ_i+▽Φ_j+▽Φ_k=0。所以f的梯度可以写成如下形式：

　　经简单计算可以求得▽Φ_i的表达式是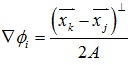，同样也可以写出▽Φ_j、▽Φ_k的表达式，其中⊥表示将向量逆时针旋转90度，A表示三角片的面积。

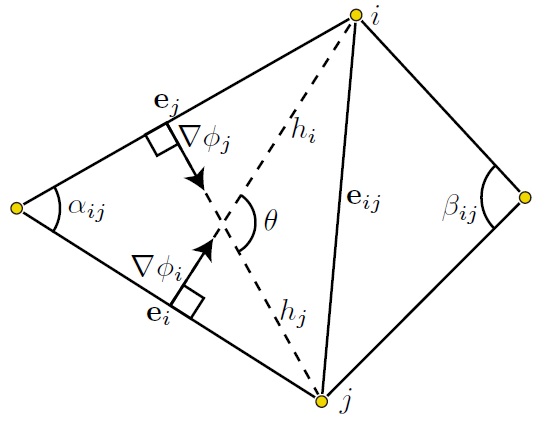
2.离散散度算子定义：

       设向量值函数w：S→R³，S表示网格，w表示在每个三角片上的向量，那么w在顶点x_i处的散度可以定义为：

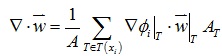
其中T(x_i)表示顶点x_i的1环邻域三角片，A_T表示三角片T的面积。

3.离散Laplace算子定义：

       将梯度算子表达式代入散度算子表达式可以得到顶点x_i处的Laplace算子如下形式：

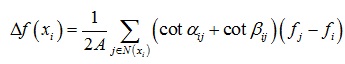
其中N(x_i)表示顶点x_i的1环邻域点。

效果：

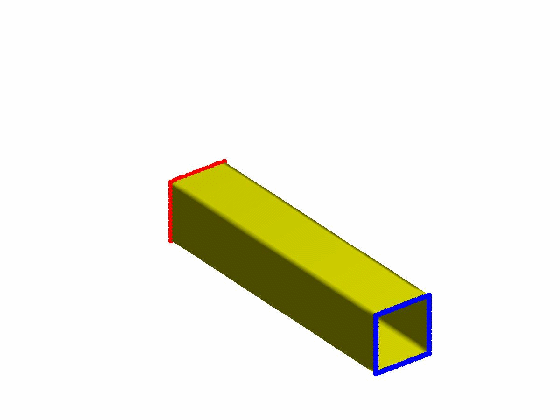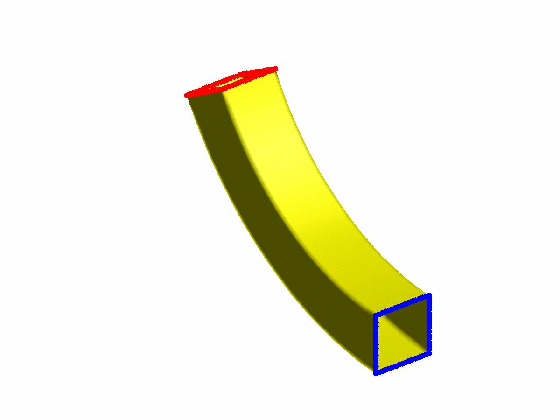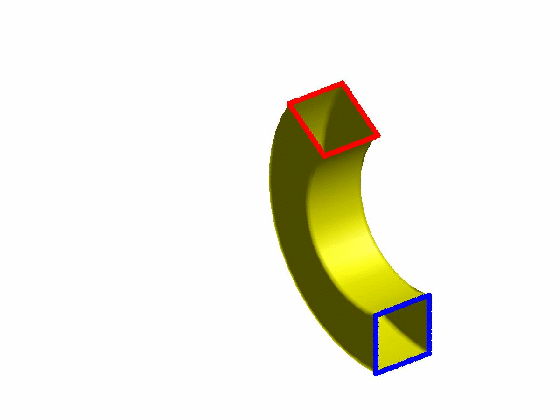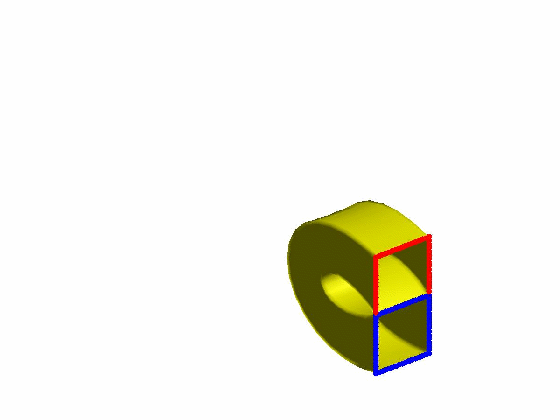
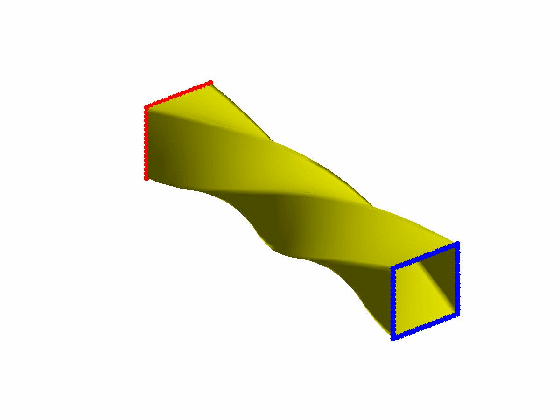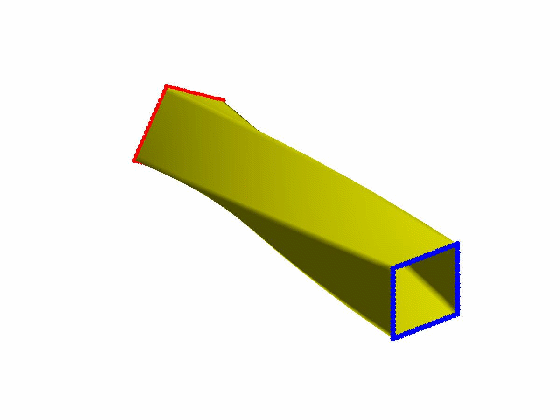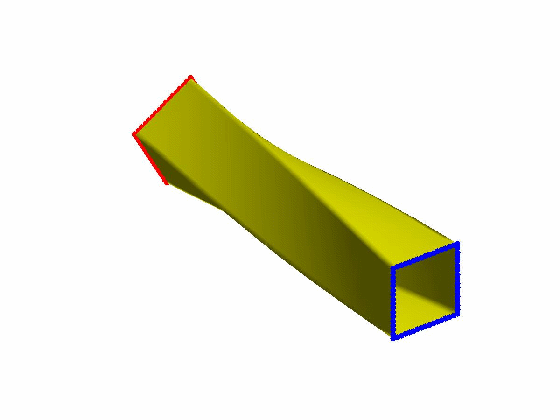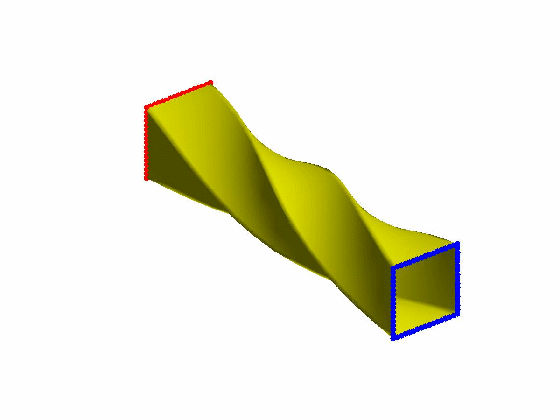
本文为原创，转载请注明出处：http://www.cnblogs.com/shushen。

参考文献：

[1] Y. Yu, K. Zhou, D. Xu, X. Shi, H. Bao, B. Guo, and H.-Y. Shum. "Mesh Editing with Poisson-Based Gradient Field Manipulation." ACM Transactions on Graphics (Proc. SIGGRAPH) 23:3 (2004), 644-51.

[2] R. Zayer, C. Rossl, Z. Karni, and H.-P. Seidel. "Harmonic Guidance for Surface Deformation." Computer Graphics Forum (Proc. Eurographics) 24:3 (2005), 601-10.

[3] 许栋. 微分网格处理技术[D]. 浙江大学, 2006.

[4] 刘昌森. 三角网格曲面上的laplace算子及其应用[D]. 中国科学技术大学, 2012.