数竞大佬jhc的三角函数复习题

班主任让数竞大佬jhc整理的三角函数复习题，我参与编辑完成。个别题目来自参考书。度盘pdf格式下载：复习题提取码419d，答案提取码5a12

---

“单纯”的运算

本文由蒋浩川原创，由\(MiserWeyte\)使用\(\LaTeX\)编辑，采用CC BY-SA 4.0协议发布。

一、公式

1、三角比

\(\sin\alpha=\dfrac{y}{r}\)
\(\cos\alpha=\dfrac{x}{r}\)
\(\tan\alpha=\dfrac{y}{x}\)

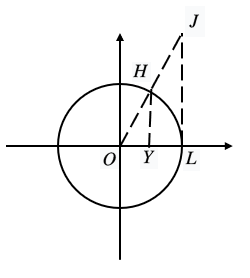
2、三角函数线

单位圆中：

\(\sin\alpha=|HY|\)
\(\cos\alpha=|OY|\)
\(\tan\alpha=|\ JL|\)

3.诱导公式xN

\(\sin(-\alpha)=-\sin\alpha\ \ \ \ \ \ \ \ \ \ \cos(-\alpha)=\cos\alpha\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \tan(-\alpha)=-\tan\alpha\)
\(\sin(\pi-\alpha)=\sin\alpha\ \ \ \ \ \ \ \ \ \cos(\pi-\alpha)=-\cos\alpha\ \ \ \ \ \ \ \ \ \tan(\pi-\alpha)=-\tan\alpha\)
\(\sin(\pi+\alpha)=-\sin\alpha\ \ \ \ \ \ \cos(\pi+\alpha)=-\cos\alpha\ \ \ \ \ \ \ \ \tan(\pi+\alpha)=\tan\alpha\)
\(\sin(\frac{\pi}{2}+\alpha)=\cos\alpha\ \ \ \ \ \ \ \ \cos(\frac{\pi}{2}+\alpha)=-\sin\alpha\ \ \ \ \ \ \ \ \tan(\frac{\pi}{2}+\alpha)=-\frac{1}{\tan\alpha}\)
\(\sin(\frac{\pi}{2}-\alpha)=\cos\alpha\ \ \ \ \ \ \ \ \cos(\frac{\pi}{2}-\alpha)=\sin\alpha\ \ \ \ \ \ \ \ \ \ \ \tan(\frac{\pi}{2}-\alpha)=\frac{1}{\tan\alpha}\)

4.和差倍半

\(\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta\)
\(\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta\)
\(\tan(\alpha+\beta)=\frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}\)

\(\sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta\)
\(\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta\)
\(\tan(\alpha-\beta)=\frac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta}\)

\(\sin2\alpha=2\sin\alpha\cos\alpha\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \sin^2\frac{\alpha}{2}=\frac{1-\cos\alpha}{2}\)
\(\cos2\alpha=\cos^2\alpha-\sin^2\alpha\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \cos^2\frac{\alpha}{2}=\frac{1+\cos\alpha}{2}\)
\(\tan2\alpha=\frac{2\tan\alpha}{1-\tan^2\alpha}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \tan^2\frac{\alpha}{2}=\frac{1-\cos\alpha}{1+\cos\alpha}\)

5.辅助角公式

\(a\sin\alpha+b\cos\alpha=\sqrt{a^2+b^2}\sin(\alpha+\varphi)\)
\(\varphi=\arctan\frac{b}{a}\)

6.其他

\(1=\sin^2\alpha+\cos^2\alpha\)
\(2\cos^2\alpha=1+\cos2\alpha\)
\(2\sin^2\alpha=1-\cos2\alpha\)

二、练习

1.已知\(\angle\alpha\)终边上一点\(P(-3m,\ 4m)\)，\(m\not=0\)，求\(\alpha\)的三个三角比

2.设\(\alpha\in(2k\pi,\ 2k\pi+\frac{\pi}{2})(\pi\in Z)\)，证明\(\sin\alpha<\alpha<\tan\alpha\)以及\(\sin\alpha+\cos\alpha>1\)

1. 设：
   \[f(x)=\begin{cases}
   \sin\pi x, \ x<0\\
   f(x-1)+1, \ x\ge0
   \end{cases}\ \ \ \ \ \ \
   g(x)=\begin{cases}
   \cos\pi x, \ x<\frac{1}{2}\\
   g(x-1)+1, \ x\ge\frac{1}{2}
   \end{cases}
   \]
   求\(f(\frac{1}{3})+f(\frac{3}{4})+g(\frac{1}{4})+g(\frac{5}{6})\)

4.求\(\dfrac{\cos(2\pi-\alpha)\cdot\tan(-\alpha-\pi)\cdot\tan(3\pi-\alpha)}{\sin(\pi-\alpha)\cdot\tan(\pi-\alpha)}\ \ \ \ \ \ \ \ (\alpha\not=k\pi+\frac{\pi}{2})\)

5.设\(k\in Z\)，求证\(\cos(k\pi+\alpha)=(-1)^k\cos\alpha\)，\(\sin(k\pi+\alpha)=(-1)^k\sin\alpha\)。

6.求\(\alpha\)：\((1)\sin\alpha=\frac{1}{2} \ \ \ \ \ \ \ (2)\tan\alpha=\frac{\sqrt{3}}{3}\)

7.已知\(\tan\alpha=2\)。求：
\((1)\dfrac{\sin\alpha+3\cos\alpha}{3\sin\alpha-4\cos\alpha}\ \ \ \ (2)\dfrac{\sin^2\alpha+8\sin\alpha\cos\alpha-6\cos^2\alpha}{3\sin^2\alpha-4\cos^2\alpha}\)

\((3)sin^2\alpha-3\sin\alpha\cos\alpha+4\cos^2\alpha-2\)

8.求\(\cos(\alpha+\frac{5}{12}\pi)\cos(\alpha+\frac{\pi}{6})+\cos(\frac{\pi}{12}-\alpha)\cos(\frac{\pi}{3}-\alpha)\)

9.已知\(\sin(\alpha+\frac{\pi}{6})=\frac{3}{5}\)，\(\alpha\in(\frac{\pi}{3}, \frac{5}{6}\pi)\)，求\(\tan(\alpha+\frac{5}{12})\)

10.若方程\(2\sin x+\sqrt5\cos x=\frac{1}{k}\)有解，求\(k\)范围。

11.求\(\sin10^\circ\cdot\sin50^\circ\cdot\sin70^\circ\)

12.\(\sin\alpha+\sin\beta=\)\(\frac{\sqrt2}{2}\)，求\(\cos\alpha+\cos\beta\)范围。

三、拓展公式

\(\sin\alpha=\dfrac{2\tan\frac{\alpha}{2}}{1+\tan^2\frac{\alpha}{2}}\ \ \ \ \ \ \ \ \ \ \cos\alpha=\dfrac{1-\tan^2\frac{\alpha}{2}}{1+\tan^2\frac{\alpha}{2}}\ \ \ \ \ \ \ \ \ \ \tan\alpha=\dfrac{2\tan\frac{\alpha}{2}}{1-\tan^2\frac{\alpha}{2}}\)

和差化积与积化和差略。

\((\sin\alpha\pm\cos\alpha)^2=1\pm\sin2\alpha\)
\((1+\tan\alpha)(1+\tan\beta)=2\Longleftrightarrow\alpha+\beta=k\pi+\frac{\pi}{4},k\in Z\)
\(\sin(\alpha+\beta)\cdot\sin(\alpha-\beta)=\sin^2\alpha-\sin^2\beta=\cos^2\beta-\cos^2\alpha\)
\(\cos(\alpha+\beta)\cdot\cos(\alpha-\beta)=\cos^2\alpha-\sin^2\beta\)

四、综合与提升

1.已知\(\alpha\in(0, \frac{\pi}{4})\)，\(\beta\in(0, 1)\)，试比较：
\(x=(\sin\alpha)^{\log_\beta\sin\alpha}\)，\(y=(\cos\alpha)^{\log_\beta\cos\alpha}\)，\(z=(\sin\alpha)^{\log_\beta\cos\alpha}\)

2.设锐角\(\theta\)使关于\(x\)的方程\(x^2+4x\cos\theta+\frac{1}{\tan\theta}=0\)有重根，求\(\theta\)。

3.求证\(\dfrac{\cos\alpha}{1+\sin\alpha}-\dfrac{\sin\alpha}{1+\cos\alpha}=\dfrac{2(\cos\alpha-\sin\alpha)}{1+\cos\alpha+\sin\alpha}\)

4.已知\(\alpha\in(-\frac{\pi}{2},\frac{\pi}{2})\)且\(\alpha\not=0\)，\(\beta\in(0, \pi)\)且\(\beta\not=\frac{\pi}{2}\)，\(\sin\alpha=\sqrt2\cos\beta\)，\(\tan\alpha\tan\beta=\sqrt3\)，求\(\alpha\)，\(\beta\)

5.已知\(\dfrac{\sin^4\alpha}{\cos^2\beta}+\dfrac{\cos^4\alpha}{\sin^2\beta}=1\)且\(\alpha,\beta\in(0,\dfrac{\pi}{2})\)，求证\(\alpha+\beta=\dfrac{\pi}{2}\)

6.求\(\cos\frac{2}{5}\pi+\cos\frac{4}{5}\pi\)

---

“单纯”的运算 参考答案

练习答案

1. (1)当\(m>0\)时，\(\sin\alpha=\frac{4}{5}\)，\(\cos\alpha=-\frac{3}{5}\)，\(\sin\alpha=-\frac{4}{3}\)
   (2)当\(m<0\)时，\(\sin\alpha=-\frac{4}{5}\)，\(\cos\alpha=\frac{3}{5}\)，\(\sin\alpha=-\frac{4}{3}\)
2. 如“三角函数线“图，\(\sin\alpha=|HY|,\alpha=\overset{\frown} {HL},\tan\alpha=|JL|\)
   \(\therefore\sin\alpha<\alpha<\tan\alpha\)
   \(\therefore\sin\alpha+\cos\alpha=|OY|+|HY|>|OH|=1\)
3. \(f(\frac{1}{3})=f(-\frac{2}{3})+1=-\frac{\sqrt3}{2}+1,\ \ f(\frac{3}{4})=f(-\frac{1}{4})+1=-\frac{\sqrt2}{2}+1\)
   \(g(\frac{1}{4})=\frac{\sqrt2}{2},\ \ g(\frac{5}{6})=\frac{\sqrt3}{2}+1\)
   \(\therefore\)所求\(=3\)
4. 原式\(=\dfrac{\cos\alpha\cdot(-\tan\alpha)\cdot(-\tan\alpha)}{\sin\alpha\cdot\tan\alpha}=1\)
5. 蒋浩川说这题显而易见，略QwQ
6. (1)\(\alpha=2k\pi+\frac{\pi}{6}\)或\(2k\pi+\frac{5}{6}\pi\ (k\in Z)\) (2)\(\alpha=k\pi+\frac{\pi}{6}\ (k\in Z)\)
7. (1)原式\(=\frac{\tan\alpha+3}{3\tan\alpha-4}=\frac{5}{2}\)(2)原式\(=\frac{\tan^2\alpha+8\tan\alpha-6}{3\tan^2\alpha-4}=\frac{7}{4}\)
   (3)原式\(=\frac{\tan^2\alpha-3\tan\alpha+2}{\tan^2\alpha+1}-2=-\frac{8}{5}\)
8. 原式\(=\cos(\alpha+\frac{\pi}{6})\sin(\frac{\pi}{12}-\alpha)+\cos(\frac{\pi}{12}-\alpha)\sin(\alpha+\frac{\pi}{6})=\sin\frac{\pi}{4}=\frac{\sqrt2}{2}\)
9. \(\tan(\alpha+\frac{5}{12}\pi)=\dfrac{1+\tan(\alpha+\frac{\pi}{6})}{1-\tan(\alpha+\frac{\pi}{6})}\ \ \ \ \ \ \because\sin(\alpha+\frac{\pi}{6})=\frac{3}{5},\alpha+\frac{\pi}{6}\in(\frac{\pi}{2},\pi)\)
   \(\therefore\tan(\alpha+\frac{\pi}{6})=-\frac{3}{4}\ \ \ \ \ \ \ \ \therefore\)所求\(=\frac{1}{7}\)
10. 左式\(=3\sin(\alpha+\theta),\theta=\arctan\frac{\sqrt5}{2}\ \ \ \ \ \ \ \\)\(\therefore\)左式\(\in[-3,3]\)
    \(\therefore-3\leq\frac{1}{k}\leq3\ \ \ \ \ \ \ \ \ \ \ \ \therefore k\in[-\infty,-\frac{1}{3}]\cup[\frac{1}{3},\infty]\)
11. 所求\(=\cos80^\circ\cos40^\circ\cos20^\circ=\dfrac{\frac{1}{8}\sin160^\circ}{\sin20^\circ}=\dfrac{1}{8}\)
12. \((\sin\alpha+\sin\beta)^2+(\cos\alpha+\cos\beta)^2=2+2\cos(x-y)\in[0,4]\)
    \(\Rightarrow\cos\alpha+\cos\beta=\pm\sqrt{2+\cos(\alpha-y)-\frac{1}{2}}\in[-\frac{\sqrt{14}}{2},\frac{\sqrt{14}}{2}]\)

综合与提升答案

1. \(\because f(x)=log_bx\)为减函数\(,b\in(0,1)\ \ \ \ \ \ \ \ 0\sin\alpha<\cos\alpha<1,\alpha\in(0,\frac{\pi}{4})\)
   \(\Rightarrow\log_b\sin\alpha>\log_b\cos\alpha>0\)
   \(\Rightarrow x<z,z<y \ \ \ \ \ \ \ \ \ \ \therefore x<z<y\)
2. 依题意\(\Delta=16\cos^2\theta-4\cot\theta=0\)且\(\cot\theta\not=0\)
   \(\therefore\Delta=4\cot\theta(2\sin2\theta-1)=0\)
   \(\Rightarrow\sin2\theta=\frac{1}{2}\Rightarrow\theta=\frac{\pi}{12}\)或\(\frac{5}{12}\pi\)
3. \(\dfrac{\cos\alpha}{1+\sin\alpha}=\dfrac{1-\sin\alpha}{\cos\alpha}=\dfrac{\cos\alpha+1-\sin\alpha}{1+\sin\alpha+\cos\alpha}\)

\(\dfrac{\sin\alpha}{1+\cos\alpha}=\dfrac{1-\cos\alpha}{\sin\alpha}=\dfrac{\sin\alpha+1-\cos\alpha}{1+\cos\alpha+\sin\alpha}\)

\(\Rightarrow\)所求证成立

1. 两式平方并作商，\(\Rightarrow\cos^2\alpha=\frac{2}{3}\sin^2\beta\)
   又\(\because\sin^2\alpha=2\cos^2\beta\)
   两式相加\(\Rightarrow2\cos^2\beta+\frac{2}{3}\sin^2\beta=1\Rightarrow\sin^2\beta=\frac{3}{4}\)
   \(\because\beta\in(0, \pi),\beta\not=\frac{\pi}{2}\ \ \ \ \ \ \ \ \therefore\sin\beta=\frac{\sqrt3}{2},\beta=\frac{\pi}{3}\)或\(\frac{2}{3}\pi\)
   \[\therefore\begin{cases}
   \alpha=\frac{\pi}{4}\\
   \beta=\frac{\pi}{3}
   \end{cases}\ \ \ 或
   \begin{cases}
   \alpha=-\frac{\pi}{4}\\
   \beta=\frac{2}{3}\pi
   \end{cases}
   \]
2. 令\(\dfrac{\sin^2\alpha}{\cos\beta}=\sin\theta\ \ \ \ \ \ \dfrac{\cos^2\alpha}{\sin\beta}=\cos\theta\ \ \ \ \ \ \theta\in(0, \dfrac{\pi}{2})\)
   \(\therefore\sin\theta\cos\beta+\sin\beta\cos\theta=\sin^2\alpha+\cos^2\alpha=1\)
   \(\Rightarrow\sin(\theta+\beta)=1\Rightarrow\sin\theta=\cos\beta\ \ \ \ \therefore\dfrac{\sin^2\alpha}{\cos\beta}=\sin\theta=\cos\beta\)
   \(\therefore\sin\alpha=\cos\beta\ \ \ \ \ \ \ \ \ \ \ \ Q.E.D.\)
3. 令\(x=\cos\frac{2}{5}\pi+\cos\frac{4}{5}\pi,y=\cos\frac{2}{5}\pi-\cos\frac{4}{5}\pi\)
   \(x\cdot y=\cos^2\frac{2}{5}\pi-\cos^2\frac{4}{5}\pi=\frac{1}{2}(1+\cos\frac{4}{5}\pi)-\frac{1}{2}(1+\cos\frac{5}{8}\pi)\)
   \(=\frac{1}{2}(\cos\frac{4}{5}\pi-\cos\frac{8}{5}\pi)=-\frac{1}{2}y\)
   \(\Rightarrow x=-\frac{1}{2}\)