poj3708：函数式化简+高精度进制转换+同余方程组

题目大意

给定一个函数

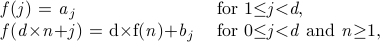
找出满足条件

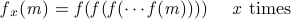  等于 k

的最小的x

m,k,d已知 其中 m，k 很大需要使用高精度存储

思路：

对 函数f(m)进行化简 ，令t=ceil( log(d,m) )

可以得到 f(m)=d ^ t * ( a [ m / (d^t) ] ) + d ^ (t-1) * ( b[ m/( d^(t-1) ) ] )......+b [m%d] ；

我们一看，每一项都是 跟 d 的次方有关，所以考虑使用 d 进制进行计算

设     m=a1b1b2b3b4（d进制）

那么  f(m)=a[a1]b[b2]b[b3]b[b4]（d进制）

以此类推

fx（m）=k，即 m通过 x次上述变换后得到了k （这里的 m 和 k 均为 d 进制）

于是 我们可以找到 m 每一位第一次等于k的情况以及这一位的循环节 分别存在数组中

那么问题就转化为了解同余方程

这个题还有很多无解的情况，需要注意特判

代码：

#include <iostream>
#include <stdio.h>
#include<string.h>
#include<algorithm>
#include<string>
#include<ctype.h>
using namespace std;
#define MAXN     100000
char m[];
char k[];
long long p[];
long long q[];
long long start[];
long long ans[];
long long res[];
long long mm[];
long long kk[];
long long a[];
long long b[];
long long d;
long long vi[];
long long getnum(char c)
{
    return c-'';
}
void trans(char* str,long long base0,long long base1)
{
    memset(res,,sizeof(res));
    long long y,i,j;
    start[]=strlen(str);
    for(i=;i<=start[];i++)
    {
        start[i]=getnum(str[i-]);
    }
    while(start[]>=)
    {
        y=; //余数
        ans[]=start[];
        for(i=;i<=start[];i++)
        {
            y=y*base0+start[i];
            ans[i]=y/base1;
            y%=base1;
        }
        res[++res[]]=y;  //这一轮的余数
        i=;
        while(i<=ans[]&&ans[i]==)
            i++;
        memset(start,,sizeof(start));
        for(j=i;j<=ans[];j++)
            start[++start[]]=ans[j];
        memset(ans,,sizeof(ans));
    }
    return;
}
long long save(long long *dis)
{
    for(long long i=res[];i;i--)
    {
        dis[res[]-i]=res[i];
    }
    return res[];
}
long long exgcd(long long a,long long b,long long &x,long long &y)
{
    if(!b)
    {
        x=;
        y=;
        return a;
    }
    long long tt=exgcd(b,a%b,x,y);
    long long t;
    t=x;
    x=y;
    y=(t-a/b*y);
    return tt;
}
long long solve(long long r)
{
    long long a1,a2,b1,b2,x,y,A,B,C,d,t;
    a1=a[];
    b1=b[];
    for(long long i=;i<r;i++)
    {
        a2=a[i];
        b2=b[i];
        A=a1;
        B=a2;
        C=b2-b1;
        d=exgcd(A,B,x,y);
        if(C%d)
        {
            return -;
        }
        t=B/d;
        x=(x*(C/d)%t+t)%t;
        b1=a1*x+b1;
        a1=a1/d*a2;
    }
    return b1;
}
int main()
{
    while(scanf("%lld",&d),d!=-)
    {
        for(long long i=;i<d;i++)
            scanf("%lld",p+i);
        for(long long i=;i<d;i++)
            scanf("%lld",q+i);
        scanf("%s%s",m,k);
        trans(m,,d);
        long long nm=save(mm);
        trans(k,,d);
        long long nk=save(kk);
        if(nm!=nk)
        {
            puts("NO");
            continue;
        }
        memset(a,-,sizeof(a));
        memset(b,-,sizeof(b));
        bool have=;
        for(long long i=;i<nm;i++)
        {
            bool ok=;
            long long tmp=;
            memset(vi,,sizeof(vi));
            for(long long j=mm[i];;)
            {
                if(j==kk[i])
                {
                    if(ok==)
                    {
                        b[i]=tmp;
                        ok=;
                    }
                    else
                    {
                        a[i]=tmp-b[i];
                        break;
                    }
                }
                tmp++;
                if(i==)
                    j=p[j];
                else
                    j=q[j];
                if(tmp>=)
                {
                    ok=;
                    break;
                }
            }
            if(!ok)
            {
                have=;
                break;
            }
        }
        if(!have)
        {
            puts("NO");
            continue;
        }
        long long ans=solve(nm);
        if(ans==-)
        {
            puts("NO");
            continue;
        }
        printf("%lld\n",ans);
    }
    return ;
}