SG函数的理解集应用

转载自知乎牛客竞赛——博弈论入门（函数讲解+真题模板）

SG函数

作用

对于一个状态i为先手必胜态当且仅当SG(i)!=0。

转移

那怎么得到SG函数尼。

SG(i)=mex(SG(j))（状态i可以通过一步转移到j）

首先说一下mex。一个集合的mex是最小的没有出现在这个集合里的非负整数。

其实想一下这个也是挺明显的。状态i是先手必败态当前仅当i转移到的状态都是先手必胜态。同样，只要当前状态可以转移到一个先手必败态，那么当前就是先手必胜态。

小定理

对于两个独立的游戏A，B，他们的SG函数=SG(A) ^ SG(B)（其实这个也是有SG函数的定义保证的）

这个比较难描述，看一下后面的题就明白了。

Nim游戏

level 1

传送门

有N堆石子。A B两个人轮流拿，A先拿。每次只能从一堆中取若干个，可将一堆全取走，但不可不取，拿到最后1颗石子的人获胜。假设A B都非常聪明，拿石子的过程中不会出现失误。给出N及每堆石子的数量，问最后谁能赢得比赛。

分析：

这就是上面那个小定理的应用了。考虑只有一堆石子的情况，肯定是先手必胜态。

SG函数肯定是石子个数(由SG的定义，显然)。

那么整个游戏的SG函数就是每个子游戏(只有一堆石子的情况)SG函数的异或之和。

所以这个题只要判断所有石子个数异或和是不是0即可。

level 2

有一堆共n个石子，Alice和Bob轮流从这堆石子里面取1到k个，不能取者输。问是否存在先手必胜策略

分析：

状态i可以转移到的状态就是i-j(1<=j<=k)

所以SG(i)=mex(SG(i-j)) (1<=j<=k)

假设k=3

则SG(0)=0,SG(1)=1,SG(2)=2,SG(3)=3,SG(4)=0,SG(5)=1...

可见，当 i%k==1时，SG(i)=0.

仔细想一下就能发现为啥了。这就相当于拿个长度为k的窗口在这个序列里面滑动。新进来的数的SG函数就是刚好从窗口的出去的那个。即先手拿x颗时，后手拿 (k+1-x) 颗。

level 3

有一堆n个石子，Alice和Bob轮流这堆石子里面取石子，每次可以取l-r个，问是否存在先手必胜态。

分析：

介绍一个通法：找规律！！

假设l=3，r=7

SG=[0,0,0,1,1,1,2,2,2,3,0,0.....]

即前 l 个为0，接着 l+r 个非0。

当然可以写个程序找

#include<bits/stdc++.h>
using namespace std;

const int maxn =  + ;
int sg[maxn], n;
int L, R;

void init_sg()
{
    for(int i = ;i < L;i++)  sg[i] = ;
    for(int i = L;i <= n;i++)
    {
        set<int>s;
        for(int j = L;j <= R;j++)
            if(i >= j)  s.insert(sg[i-j]);
        int t = ;
        while(s.count(t)) t++;
        sg[i] = t;
    }
}

int main()
{
    L = , R = ;
    n = ;
    init_sg();
    for(int i = ;i < n;i++)
    {
        printf("%d ", sg[i]);
        if(i % (L+R) == (L+R-))  printf("\n");
    }
}

可写成SG(i)=i%(l + r) / l，但是要怎么证明呢？

一般可以用数学归纳法证明！

level 4

有n堆石子，第i堆石子有a[i]个，Alice和Bob轮流操作，每次可以从一堆石子里面取任意多个，也可以把一堆石子分成两堆。不能操作者输。问是否存在先手必胜态。

分析

继续找规律！

SG(i)=mex(SG(i - j),SG(i-j) ^ SG(j))

SG(i-j)是从石子里面取j个，SG(i-j)^SG(j)是将石子分成j和i-j两堆。

level 5

有1堆石子,Alice和Bob轮流操作，每次可以从一堆里面取当前个数的因数个(不能是本身)，不能操作者(剩下一个)输。问是否存在先手必胜态。

分析：

SG(i) = mex(SG(i-k)) (k|i)

打表如下：

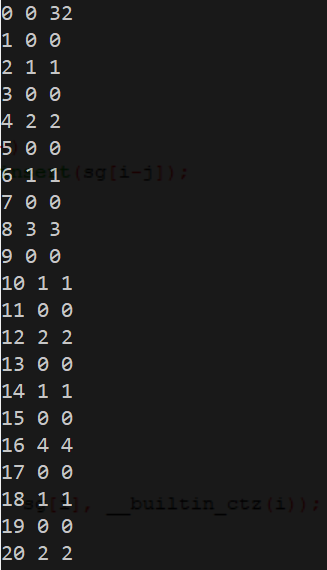
找规律可以发现

SG(i) = __builtin_ctz(i)

也就是i的末尾0的个数

level 6

有1堆石子，Alice和Bob轮流操作，每次可以从一堆里面取与当前个数互质的数字个石子，不能操作者输，问是否存在先手必胜态

分析：

SG(i)=mex(SG(i-j)) (gcd(i,j)=1)

打表如下：

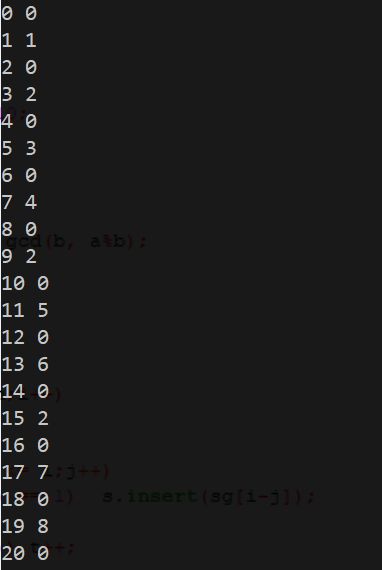
发现，对于偶数，SG为0.

对于奇数，SG为最小质因子的编号(就是最小质因子是第几个质数)