迭代硬阈值类（IHT）算法总结

斜风细雨作小寒，淡烟疏柳媚晴滩。入淮清洛渐漫漫。

雪沫乳花浮午盏，蓼茸蒿笋试春盘。人间有味是清欢。

---- 苏轼

更多精彩内容请关注微信公众号 “优化与算法”

迭代硬阈值（Iterative Hard Thresholding）算法是求解基于 ${\ell _0}$ 范数非凸优化问题的重要方法之一，在稀疏估计和压缩感知重构等领域应用较多。IHT最初由Blumensath, Thomas等人提出，后来许多学者在IHT算法的基础上不断发展出一些改进算法，如正规化迭代硬阈值算法（Normalized Iterative Hard Thresholding, NIHT)、共轭梯度硬阈值迭代算法（Conjugate Gradient Iterative Hard Thresholding, CGIHT）、基于回溯的硬阈值迭代算法（Backtracking based Iterative Hard Thresholding）等，以及后来与贪婪算法结合产生的一些算法，如硬阈值追踪算法（Hard Thresholding Pursuit, HTP）就是结合子空间追踪算法（SP）和IHT算法的优势得到的。

笔者在此将上述这些算法原理做简要分析，并附上算法和测试代码供参考。

1. 迭代硬阈值算法

1.1 IHT算法描述

以稀疏近似问题为例，介绍IHT算法。对于以下优化问题：

\[\mathop {\min }\limits_{\bf{x}} \left\| {{\bf{y}} - {\bf{Ax}}} \right\|_2^2{\rm{ }} ~~~~~~s.t.~~~~~{\rm{ }}{\left\| {\bf{x}} \right\|_0} \le S~~~~~~~~~~~~(1)
\]

其中 ${\bf{y}} \in {{\bf{R}}^M}$, ${\bf{A}} \in {{\bf{R}}^{M \times N}}$，且 $M < N$， ${\left\| {\bf{x}} \right\|_0}$ 为 $\bf{x}$ 的 ${\ell _0}$ 范数，表示 $\bf{x}$ 中非零元素的个数。由于 $M < N$，显然（1）式是一个欠定问题，加上 ${\ell _0}$ 约束，式（1）同时是个组合优化问题，无法在多项式时间复杂度内求解。

为了求解优化问题（1），Blumensath 等人提出了著名的 IHT 算法，其迭代格式为：

\[{{\bf{x}}_{k + 1}} = {H_k}({{\bf{x}}_k} + {{\bf{A}}^{\mathop{\rm T}\nolimits} }({\bf{y}} - {\bf{A}}{{\bf{x}}_k}))~~~~~~~~~~~~~~~~(2)
\]

其中 ${H_S}( \cdot )$ 表示取 $\cdot$ 中最大的 $S$ 个非零元素。

式(2)看起来并不复杂，直观上来看就是对（1）式用常数步长的梯度下降法来求解，其中在每次迭代中对更新的结果进行一次硬阈值操作。为什么硬阈值操作+梯度下降可以求解(1)式的 ${\ell _0}$ 范数优化问题呢？文献[1]中作者利用Majorization-Minimization优化框架推导出了（2）式所示迭代公式，并证明了IHT算法在 ${\left\| {\bf{A}} \right\|_2} < 1$ 时，算法能收敛到局部最小值。以下对IHT算法的原理做简要分析。

1.2 Majorization-Minimization优化框架

首先简单介绍一下MM优化框架，实际上MM优化框架是处理非凸优化问题中常见的一种方法，其形式简单，思想优雅。后期关于MM思想再以专题形式进行详细的总结和讨论。

(1) 式的目标函数为

\[{F}({\bf{x}}) = \left\| {{\bf{y}} - {\bf{Ax}}} \right\|_2^2 ~~~~~~~~~~~~~~~~~~~~~~~~~~~(3)
\]

(1) 无法得到一个闭式解，只能用迭代方法来求得一个近似解。

MM优化思想：当目标函数 $F({\bf{x}})$ 比较难优化时，通常可以选择更容易优化的替代目标函数 $G({\bf{x}})$，当 $G({\bf{x}})$ 满足一定的条件时，$G({\bf{x}})$ 的最优解能够无限逼近原目标函数 $F({\bf{x}})$ 的最优解。这样的 $G({\bf{x}})$ 需要满足3个条件：

容易优化
对所有 $\bf{x}$，$G({\bf{x}}) \ge F({\bf{x_{k}}})$
${G_k}({{\bf{x}}_k}) = F({{\bf{x}}_k})$

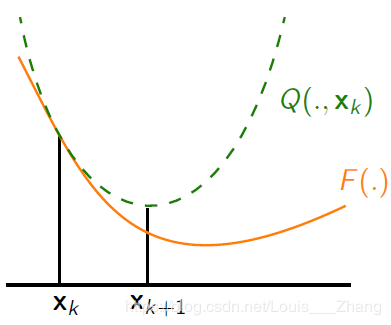
在满足 ${\left\| {\bf{A}} \right\|_2} < 1$ 条件时，目标函数 (4) 可用如下替代目标函数来代替：

\[G({\bf{x}},{\bf{z}}) = \left\| {{\bf{y}} - {\bf{Ax}}} \right\|_2^2 - \left\| {{\bf{Ax}} - {\bf{Az}}} \right\|_2^2 + \left\| {{\bf{x}} - {\bf{z}}} \right\|_2^2~~~~~~~(4)
\]

从 (4) 式可以看出，替代目标函数 $G({\bf{x}},{\bf{z}})$ 是满足MM优化框架中所列条件的。

对式 (4) 展开并化简：

\[\eqalign{
& G({\bf{x}},{\bf{z}}) = \left\| {{\bf{y}} - {\bf{Ax}}} \right\|_2^2 - \left\| {{\bf{Ax}} - {\bf{Az}}} \right\|_2^2 + \left\| {{\bf{x}} - {\bf{z}}} \right\|_2^2 \cr
& = \left( {\left\| {\bf{y}} \right\|_2^2 - 2{{\bf{x}}^{\mathop{\rm T}\nolimits} }{{\bf{A}}^{\mathop{\rm T}\nolimits} }{\bf{y}} + \left\| {{\bf{Ax}}} \right\|_2^2} \right) - \left( {\left\| {{\bf{Ax}}} \right\|_2^2 - 2{{\bf{x}}^{\mathop{\rm T}\nolimits} }{{\bf{A}}^{\mathop{\rm T}\nolimits} }{\bf{Az}} + \left\| {{\bf{Az}}} \right\|_2^2} \right) + \left( {\left\| {\bf{x}} \right\|_2^2 - 2{{\bf{x}}^T}{\bf{z}} + \left\| {\bf{z}} \right\|_2^2} \right) \cr
& = \left[ {\left\| {\bf{x}} \right\|_2^2 - \left( {2{{\bf{x}}^T}{\bf{z}} + 2{{\bf{x}}^T}{{\bf{A}}^{\mathop{\rm T}\nolimits} }{\bf{y}} - 2{{\bf{x}}^T}{{\bf{A}}^{\mathop{\rm T}\nolimits} }{\bf{Az}}} \right)} \right] + \left\| {\bf{y}} \right\|_2^2 + \left\| {\bf{z}} \right\|_2^2 + \left\| {{\bf{Az}}} \right\|_2^2 \cr
& = \left[ {\left\| {\bf{x}} \right\|_2^2 - 2{{\bf{x}}^T}\left( {{\bf{z}} + {{\bf{A}}^{\mathop{\rm T}\nolimits} }{\bf{y}} - {{\bf{A}}^{\mathop{\rm T}\nolimits} }{\bf{Az}}} \right)} \right] + \left\| {\bf{y}} \right\|_2^2 + \left\| {\bf{z}} \right\|_2^2 + \left\| {{\bf{Az}}} \right\|_2^2 \cr
& = \sum\limits_i {\left[ {{\bf{x}}_i^2 - 2{{\bf{x}}_i}\left( {{{\bf{z}}_i} + {\bf{A}}_i^{\mathop{\rm T}\nolimits} {\bf{y}} - {\bf{A}}_i^{\mathop{\rm T}\nolimits} {\bf{Az}}} \right)} \right]} + \left\| {\bf{y}} \right\|_2^2 + \left\| {\bf{z}} \right\|_2^2 + \left\| {{\bf{Az}}} \right\|_2^2 \cr} \]

上式的最后三项是与 $\bf{x}$ 无关的项，对优化结果没有影响，那么使 (5) 式最小化等价于下式最小化：

\[G'({\bf{x}},{\bf{z}}) = \sum\limits_i {\left[ {{\bf{x}}_i^2 - 2{{\bf{x}}_i}\left( {{{\bf{z}}_i} + {\bf{A}}_i^{\mathop{\rm T}\nolimits} {\bf{y}} - {\bf{A}}_i^{\mathop{\rm T}\nolimits} {\bf{Az}}} \right)} \right]} ~~~~~~~~~~~~~~~~~~~~(5)
\]

对 (5) 式进行配方，可以得到：

\[\eqalign{
& G'({\bf{x}},{\bf{z}}) = \sum\limits_i {\left[ {{\bf{x}}_i^2 - 2{{\bf{x}}_i}\left( {{{\bf{z}}_i} + {\bf{A}}_i^{\mathop{\rm T}\nolimits} {\bf{y}} - {\bf{A}}_i^{\mathop{\rm T}\nolimits} {\bf{Az}}} \right)} \right]} \cr
& = \sum\limits_i {\left[ {{\bf{x}}_i^2 - 2{{\bf{x}}_i}\left( {{{\bf{z}}_i} + {\bf{A}}_i^{\mathop{\rm T}\nolimits} {\bf{y}} - {\bf{A}}_i^{\mathop{\rm T}\nolimits} {\bf{Az}}} \right) + \left( {{{\bf{z}}_i} + {\bf{A}}_i^{\mathop{\rm T}\nolimits} {\bf{y}} - {\bf{A}}_i^{\mathop{\rm T}\nolimits} {\bf{Az}}} \right) - \left( {{{\bf{z}}_i} + {\bf{A}}_i^{\mathop{\rm T}\nolimits} {\bf{y}} - {\bf{A}}_i^{\mathop{\rm T}\nolimits} {\bf{Az}}} \right)} \right]} \cr
& = \sum\limits_i {\left\{ {{{\left[ {{\bf{x}}_i^2 - \left( {{{\bf{z}}_i} + {\bf{A}}_i^{\mathop{\rm T}\nolimits} {\bf{y}} - {\bf{A}}_i^{\mathop{\rm T}\nolimits} {\bf{Az}}} \right)} \right]}^2} - {{\left( {{{\bf{z}}_i} + {\bf{A}}_i^{\mathop{\rm T}\nolimits} {\bf{y}} - {\bf{A}}_i^{\mathop{\rm T}\nolimits} {\bf{Az}}} \right)}^2}} \right\}} \cr} \]

令 ${{\bf{x}}^*} = {{\bf{z}}_i} + {\bf{A}}_i^{\mathop{\rm T}\nolimits} \left( {{\bf{y}} - {\bf{Az}}} \right)$，得：

\[\sum\limits_i {\left[ {{\bf{x}}_i^2 - \left( {{{\bf{z}}_i} + {\bf{A}}_i^{\mathop{\rm T}\nolimits} {\bf{y}} - {\bf{A}}_i^{\mathop{\rm T}\nolimits} {\bf{Az}}} \right)} \right]} = \sum\limits_i {\left\{ {{{\left[ {{{\bf{x}}_i} - {{\bf{x}}^*}} \right]}^2} - {{\left( {{{\bf{x}}^*}} \right)}^2}} \right\}}
\]

即当 ${{{\bf{x}}_i} = {{\bf{x}}^*}}$ 时， $G'({\bf{x}},{\bf{z}})$ 取得最小值，且最小值等于 $\sum\limits_i - {\left( {{{\bf{x}}^*}} \right)^2}$ 。

结合式 (1) 中的 ${\ell _0}$ 范数约束项，最小化 $G'({\bf{x}},{\bf{z}})$ 变成如何使得在 $\bf{x}$ 中非零元素个数小于 $S$ 的情况下，最小化 $\sum\limits_i - {\left( {{{\bf{x}}^*}} \right)^2}$。很容易想到，只需要保留 $\bf{x}$ 中前 $S$ 个最大项即可，这可以通过硬阈值函数来进行操作。

1.3 硬阈值函数

硬阈值函数如下所示：

\[{H_S}({{\bf{x}}_i}) = \left\{ {\matrix{
{0{\rm{~~~~~if~~~}}\left| {{{\bf{x}}_i}} \right| < T} \cr
{{{\bf{x}}_i}{\rm{~~~if~~~}}\left| {{{\bf{x}}_i}} \right| \ge T} \cr
} } \right.\]

其中 $T$ 为 $abs\left[ {{{\bf{x}}_k} + {{\bf{A}}^{\mathop{\rm T}\nolimits} }({\bf{y}} - {\bf{A}}{{\bf{x}}_k})} \right]$ 按从大到小排列第 $S$ 个值的大小。

硬阈值函数如下图所示，这跟前面介绍的软阈值函数类似。

1.4 IHT算法程序

function [hat_x] = cs_iht(y,A,K,itermax,error)
% Email: zhangyanfeng527@gmail.com
% Reference: Blumensath T, Davies M E. Iterative hard thresholding for compressed sensing[J].
% Applied & Computational Harmonic Analysis, 2009, 27(3):265-274.
% y: measurement (observe) vector
% A: measurement (sensing) matrix
% k: sparsity level
% 注意，IHT算法需要norm(A)<1,否则结果很不稳定，甚至不收敛。
u = 1 ; % 默认步长等于1，也可以自己选择
x0 = zeros(size(A,2),1) ;         % initialization with the size of original
for times = 1 : itermax
    x_increase = A' * (y - A * x0);
    hat_x = x0 + u * x_increase ;
    [~,pos] = sort(abs(hat_x),'descend');
    hat_x(pos(K + 1 : end)) = 0 ;   % thresholding, keeping the larges s elements
    if norm(y - A * hat_x) < error || norm(x0-hat_x)/norm(hat_x) < error
        break ;
    else
        x0 = hat_x ;          % update
    end
end

2. NIHT算法

由于IHT算法需要满足 ${\left\| {\bf{A}} \right\|_2} < 1$，因此算法对 ${\left| {\bf{A}} \right|_2} $ 的缩放很敏感，当不满足此条件时，迭代过程会严重动荡甚至不收敛。此外，IHT算法固定步长为1，无法更好的利用自适应步长加速算法的收敛，而通过调节步长来实现算法收敛加速显然不现实。

基于以上原因，Blumensath, Thomas 等人接下来又提出了正规化硬阈值迭代算法，NIHT算法的优势是利用李普希兹连续条件来规范化步长，使算法不受矩阵 $\bf{A}$ 缩放的影响。同时采用一维线搜索，推导出自适应步长公式，使迭代次数大幅减少。这种方式以少量可不计的计算量增加换来了算法收敛速度的大幅提升。

NIHT算法具体的原理在此不细述，感兴趣的朋友可以参考文献[2]，此处供上原文中的算法伪代码：

NIHT算法程序如下：

function [x_p] = cs_niht(y,A,K，itermax,error,par_c)
% Email: zhangyanfeng527@gmail.com
% Reference: Blumensath T, Davies M E. Normalized Iterative Hard Thresholding: Guaranteed Stability and Performance[J].
% IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2):298-309.
% y: measurement (observe) vector
% A: measurement (sensing) matrix
% k: sparsity level
% itermax: max iteration
% error: error threshold
% par_c: 0 < par_c < 1
% NIHT算法的好处是使用自适应的步长，不再像IHT那样要求norm(A)<1了
x0 = zeros(size(A,2),1);         % initialization with the size of original
g0 = A' * y ;
u = norm(g0) / norm(A * g0) ;
x1 = x0 + u * g0 ;
[~,pos1] = sort(abs(x1),'descend') ;
x1(pos1(K + 1:end)) = 0 ;
gamma0 = find(x1) ;
for times = 1 : itermax
    g1 = A' * (y - A * x1) ; % calculate gradient
    u = norm(g1(gamma0)) / norm(A(:,gamma0) * g1(gamma0)) ;  % calculate step size
    x_p = x1 + u * g1 ;
    [~,pos1] = sort(abs(x_p),'descend') ;
    x_p(pos1(K + 1 : end)) = 0 ;
    gamma1 = find(x_p) ;   % support set
    W = ( norm ( x_p - x1 ) )^2 / ( norm(A * (x_p - x1)) )^2 ;
    if isequal(gamma0,gamma1) == 1
    elseif isequal(gamma0,gamma1) == 0
    % normalized step size
        if u <= 1 * W
        elseif u > 1 * W
            while(u > 1 * W )
                u = par_c * u ;
            end
            x_p = x1 + u * g1 ;
            [~,pos1] = sort(abs(x_p),'descend') ;
            x_p(pos1(K + 1 : end)) = 0 ;
            gamma1 = find(x_p) ;
        end
    end
    if  norm(y - A * x_p) < error
        break;
    else
        x1 = x_p ;          % update
        gamma0 = gamma1 ;
    end
end

3. CGIHT算法

尽管NIHT算法在IHT算法的基础上改进了不少地方，但是总的来说，IHT算法和NIHT算法都是基于梯度的算法，只利用了梯度域的信息，而梯度下降法本身收敛速度受限。为了进一步提高IHT算法的收敛速度，Blanchard, Jeffrey D等人提出使用共轭梯度来代替IHT算法中的梯度，并证明了CGIHT算法的收敛速度比IHT算法快。具体可以描述为，IHT算法和NIHT算法是基于梯度的算法，其收敛速度与

\[{{K - 1} \over {K + 1}}
\]

有关，而CGIHT算法使用共轭梯度，其收敛速度与

\[{{\sqrt K - 1} \over {\sqrt K + 1}}
\]

有关。其中 $K$ 是矩阵 ${{{\bf{A}}^{\mathop{\rm T}\nolimits} }{\bf{A}}}$ 的条件数。很显然后者小于前者，因此其收敛速度更快。

CGIHT算法的原理比较简单，这里不再详细介绍，下面是原文中CGIHT算法的伪代码：

CGIHT算法程序如下：

function [x_p] = cs_cgiht(y,A,s,itermax,error)
% Emial: zhangyanfeng527@gmail.com
% Reference: Blanchard J D, Tanner J, Wei K. CGIHT: conjugate gradient iterative hard thresholding
% for compressed sensing and matrix completion[J].
% Information & Inference A Journal of the Ima, 2015(4).
% y: measurement (observe) vector
% A: measurement (sensing) matrix
% s: sparsity level
% itermax: max iteration
% error: error threshold
x_0 = .2 * ones(size(A,2),1);         % initialization with the size of original
g0 = A' * ( y - A * x_0) ;
[~,pos0] = sort(abs(g0),'descend') ;
g0(pos0(s+1:end)) = 0 ;
d0 = g0 ;
u = (norm(g0) / norm(A * d0))^2 ;
x_1 = x_0 + u * d0 ;
[~,pos1] = sort(abs(x_1),'descend');
x_1(pos1(s + 1 : end)) = 0 ;
gamma1 = find(x_1) ;
%% restart CGIHT algorithm
% tao = gamma1 ;
% for times = 1 : itermax
%     g1 =  A' * ( y - A * x_1) ;
%     if isequal(gamma0,tao) == 1
%         u = (g1(gamma1)' * g1(gamma1)) / (g1(gamma1)' * A(:,gamma1)' * A(:,gamma1) * g1(gamma1)) ;
%         x_p = x_1 + u * g1 ;
%     else
%         belta = (norm(g1) / (norm(g0)))^2;
%     d1 = g1 + belta * d0 ;
%     u = (d1(gamma1)' * g1(gamma1)) / (d1(gamma1)' * A(:,gamma1)' * A(:,gamma1) * d1(gamma1)) ;
%     x_p = x_1 + u * d1 ;
%     end
%     [~,index] = sort(abs(x_p),'descend');
%     x_p(index(s + 1 : end)) = 0 ;
%     if norm(x_p - x_1)/norm(x_p)< error || norm(y - A * x_p)<error
%         break;
%     else
%         gamma0 = gamma1 ;
%         gamma1 = index ;
%         x_1 = x_p ;
%     end
% end
%% CGIHT algorithm
for times = 1 : itermax
    g1 =  A' * ( y - A * x_1) ;
    belta = (norm(g1) / (norm(g0)))^2 ;
    d1 = g1 + belta * d0 ;
    u = (d1(gamma1)' * g1(gamma1)) / (d1(gamma1)' * A(:,gamma1)' * A(:,gamma1) * d1(gamma1)) ;
    x_p = x_1 + u * d1 ;
    [~,index] = sort(abs(x_p),'descend') ;
    x_p(index(s + 1 : end)) = 0 ;
    if norm(x_p - x_1)/norm(x_p)< error || norm(y - A * x_p)<error
        break;
    else
        x_1 = x_p ;
        g0 = g1 ;
        d0 = d1 ;
    end
end
end

4. HTP 算法

硬阈值追踪算法（Hard Thresholding Pursuit HTP）是由SIMON FOUCART提出来的，该算法结合了子空间追踪算法（Subspace Pursuit SP）算法和IHT算法的优势，一方面具备更强的理论保证，另一方面也表现出良好的实证效果。

与IHT算法不同的是，HTP算法在每次迭代中采用了SP算法中用最小二乘更新稀疏系数的方法，最小二乘是一种无偏估计方法，这使得更新结果更加精确，从而可以减少迭代次数。

与SP算法不同的是，SP算法在每次迭代中是采用测量矩阵与残差的内积（即${{{\bf{A}}^T}({\bf{y}} - {\bf{Ax}})}$）的大小来挑选最大的 $S$ 个支撑位置，而HTP算法则是像IHT算法一样采用 ${{\bf{x}}{\rm{ + }}{{\bf{A}}^T}({\bf{y}} - {\bf{Ax}})}$ 来挑选支撑，后者无疑比前者包含更多的信息，因此相对于SP算法，HTP算法能更快的找到支撑位置，从而减少迭代次数。

总的说来，HTP算法是结合了IHT算法和SP算法的优势，因此其表现也更好。HTP算法原理较为简单，在此不详细介绍，对SP算法的介绍在后续贪婪类算法中一并总结。

下面是HTP算法的伪代码：

HTP算法的程序如下：

function [hat_x] = cs_htp(y,A,K,itermax,error)
% Emial: zhangyanfeng527@gmail.com
% Reference: Foucart S. HARD THRESHOLDING PURSUIT: AN ALGORITHM FOR COMPRESSIVE SENSING[J].
% Siam Journal on Numerical Analysis, 2011, 49(6):2543-2563.
% y: measurement (observe) vector
% A: measurement (sensing) matrix
% k: sparsity level
x0 = .2 * ones(size(A,2),1) ;         % initialization with the size of original
u = 1 ; % stpesize=1
for times = 1 : itermax
    x_increase = A' * (y - A * x0);
    hat_x = x0 + u * x_increase ;
    [~,pos] = sort(abs(hat_x),'descend');
    gamma = pos(1:K) ;
    z = A(:,gamma) \ y ;
    hat_x = zeros(size(A,2),1) ;
    hat_x(gamma) = z ;
    if norm(y - A * hat_x) < error || norm(hat_x-x0)/norm(hat_x) < error
        break;
    else
        x0 = hat_x ;
    end
end
end

5. 仿真

以下对上述四种算法进行重构效果比较，测试程序如下：

%% CS reconstruction test
% Emial: zhangyanfeng527@gmail.com
clear
clc
close all
M = 64 ; %观测值个数
N = 256 ; %信号x的长度
K = 10 ; %信号x的稀疏度
Index_K = randperm(N) ;
x = zeros(N,1) ;
x(Index_K(1:K)) = 5 * randn(K,1); % x为K稀疏的，且位置是随机的
Psi = eye(N); % x本身是稀疏的，定义稀疏矩阵为单位阵x=Psi*theta
Phi = randn(M,N); %测量矩阵为高斯矩阵
Phi = orth(Phi')';
A = Phi * Psi; %传感矩阵
% sigma = 0.005;
% e = sigma*randn(M,1);
% y = Phi * x + e;%得到观测向量y
y = Phi * x ; %得到观测向量y
%% 恢复重构信号x
tic
theta = cs_iht(y,A,K);
x_r = Psi * theta;% x=Psi * theta
toc
%% 绘图
figure;
plot(x_r,'k.-');%绘出x的恢复信号
hold on;
plot(x,'r');%绘出原信号x
hold off;
legend('Recovery','Original')
fprintf('\n恢复残差：');
norm(x_r-x)%恢复残差

上述测试脚本只提供了简单的实验设置，对算法重构成功率、算法迭代次数与误差的关系（收敛速度）、重构时间、鲁棒性等测试可以自由发挥。

参考文献

[1] Blumensath, Thomas, and Mike E. Davies. "Iterative hard thresholding for compressed sensing." Applied and computational harmonic analysis 27.3 (2009): 265-274.

[2] Blumensath, Thomas, and Mike E. Davies. "Normalized iterative hard thresholding: Guaranteed stability and performance." IEEE Journal of selected topics in signal processing 4.2 (2010): 298-309.

[3] Blanchard, Jeffrey D., Jared Tanner, and Ke Wei. "CGIHT: conjugate gradient iterative hard thresholding for compressed sensing and matrix completion." Information and Inference: A Journal of the IMA 4.4 (2015): 289-327.

[4] Foucart, Simon. "Hard thresholding pursuit: an algorithm for compressive sensing." SIAM Journal on Numerical Analysis 49.6 (2011): 2543-2563.