CMU Database Systems - Sorting，Aggregation，Join

Sorting

排序如果可在内存里面排，用经典的排序算法就ok，比如快排

问题在于，数据表中的的数据是很多的，没法一下都放到内存里面进行排序

所以就需要用到，外排，多路并归排序

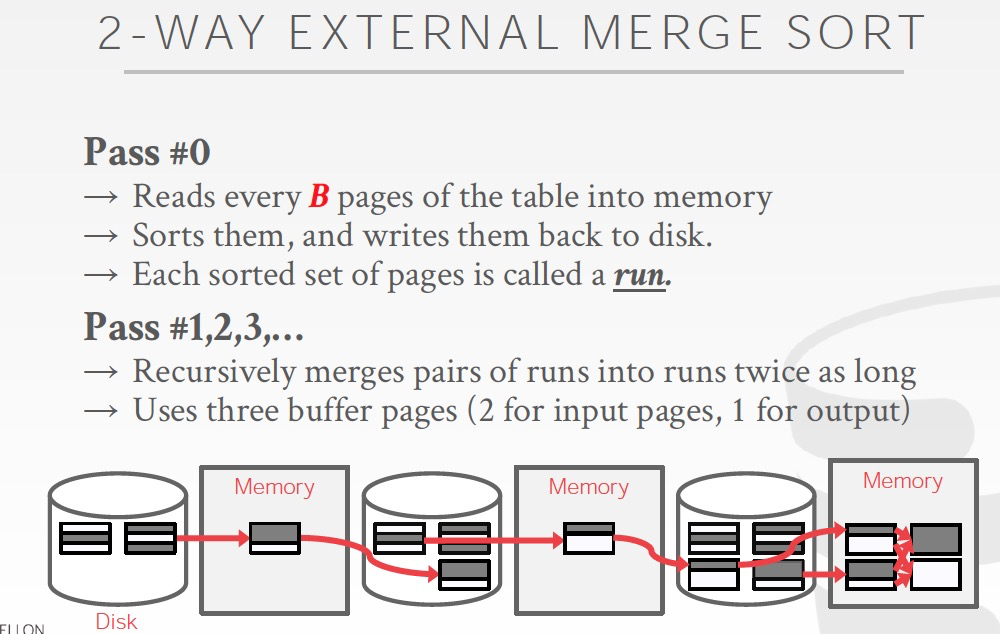
看下最简单的，2路并归排序，

设文件分为N个page，memory中一次最多可以放入B个pages

所以在sort过程，一次性可以载入B个page，在内存中page内排序，写回disk，称为一轮，run
那么如果一共N个page，需要N/B+1个run

在merge过程，如果双路并归排序，只需要用到3个page的buffer，多了也没用

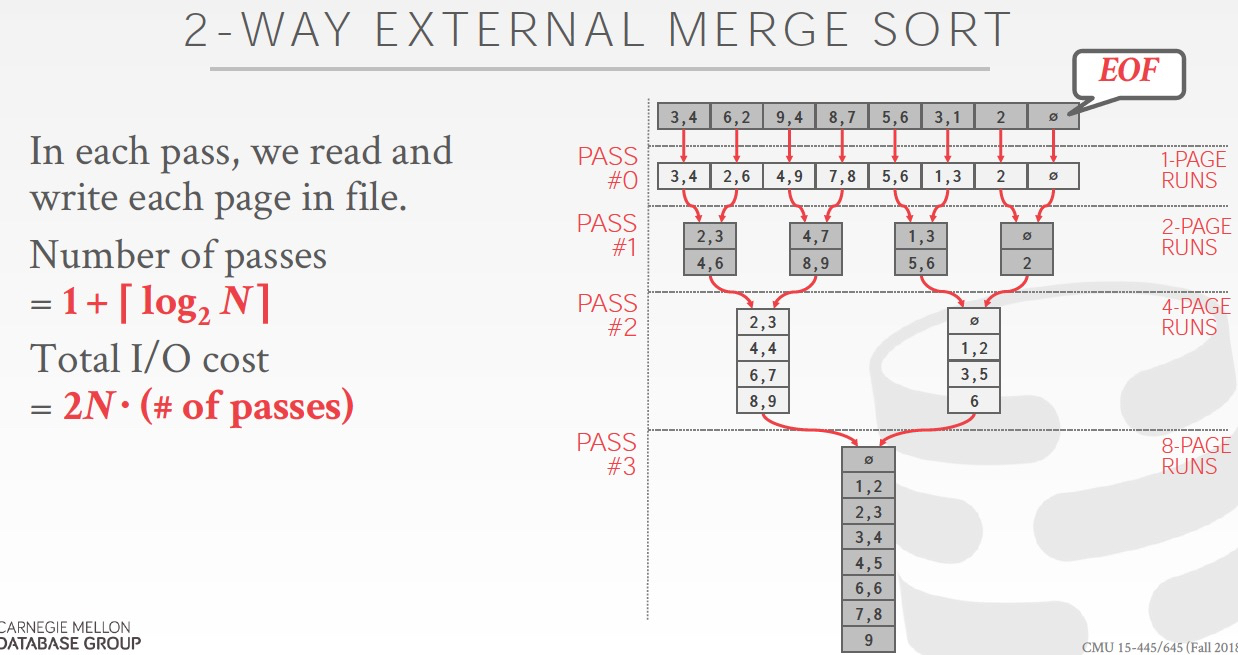
Merge过程的cost

每个pass都需要读写一遍所有的数据，cost为2N
2 way，所以一共有1 + logN个pass

多路并归排序的通用公式如下，

其他都比较容易理解，为什么way数是B-1？

因为memory一共B个buffer，需要留一个output，剩下的用于merge，所以最多是B-1路并归排序

如果我们有B+ index的情况下，

分两种情况，要排序的字段有Clustered B+索引，那么直接从左到右遍历叶子节点就好

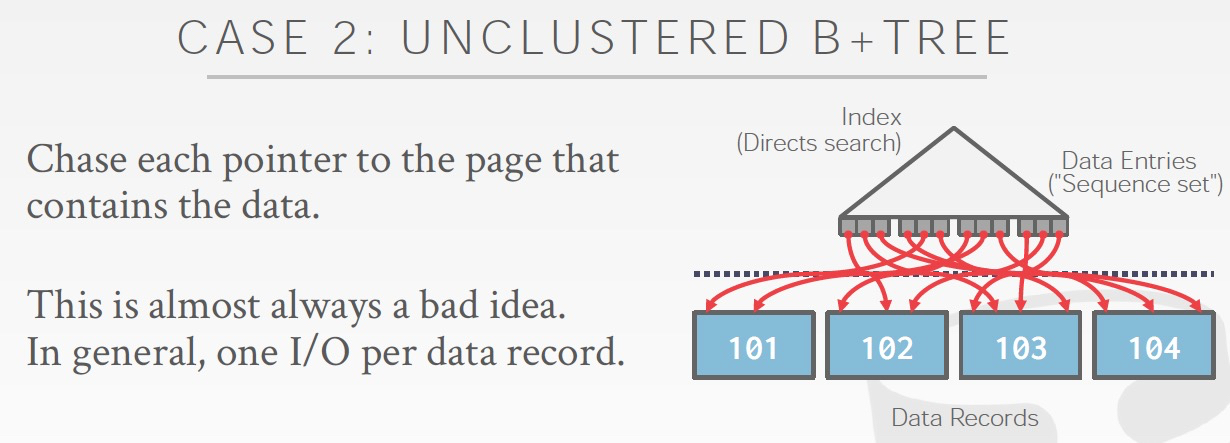
排序的字段不是Clustered B+索引，比如是secondary 索引

那么从索引里面只能获取到排好序的id，然后要通过id去Clustered B+索引中取真正的value，效率也很低，每个record都需要一次io

Aggregation

Aggregation有两种思路，

一种先排序sorting，然后再按顺序做aggregate

这个方法明显的问题，就是比较费，有些场景不需要sort，比如group by，distinct

所以第二种思路是Hashing，

在memory里面临时维护一个hash table，去重或聚合都在hash table上完成

问题就是，如果hash table太大，内存放不下怎么办？

所以解法的思路，放不下，就切开，切成能放下的一个个partition，并且要保证一个key的数据都在一个partition里面，这样只要保证内存能够放下一个partition就可以aggregate，不需要去读其他的partition

第一次partition划分成几个partition，如果内存B个buffer，划分成B-1个partition；如果划分完了某个partition还是放不下怎么办，那就继续划分，直到所有partition都可以放到内存中

这里有几个问题，

首先，一个partition应该不止一个key，如果只有一个，第二步里面的h2感觉没用
第二，假设数据是均匀分布的，不会出现太大的倾斜，不会有partition overflow

Join

为什么需要join？

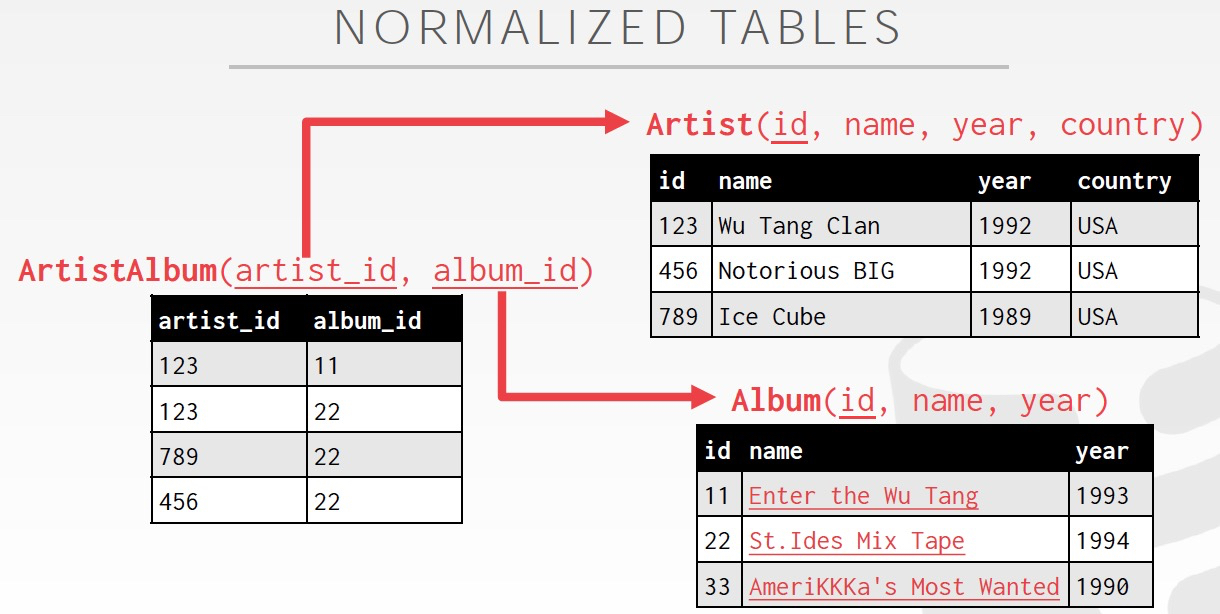
因为不同的数据存在不同的表里面，所以要查询就需要关联
那么为什么不能放在一张表里面，关系表的设计有范式的要求，避免大量的数据重复

Join Operator Output

直接输出data，这样好处是，后续operator不用回到数据表再去读数据
这个方法比较实用于TP需求，结果数据较少的情况

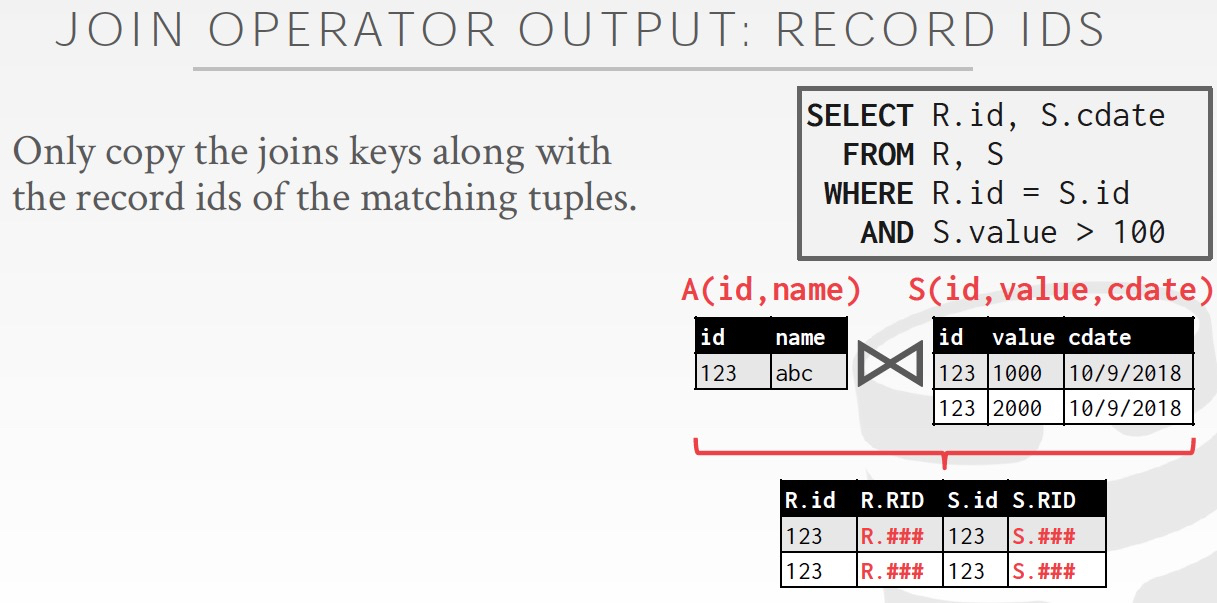
仅仅输出ids，适合AP需求，join结果集非常大的情况

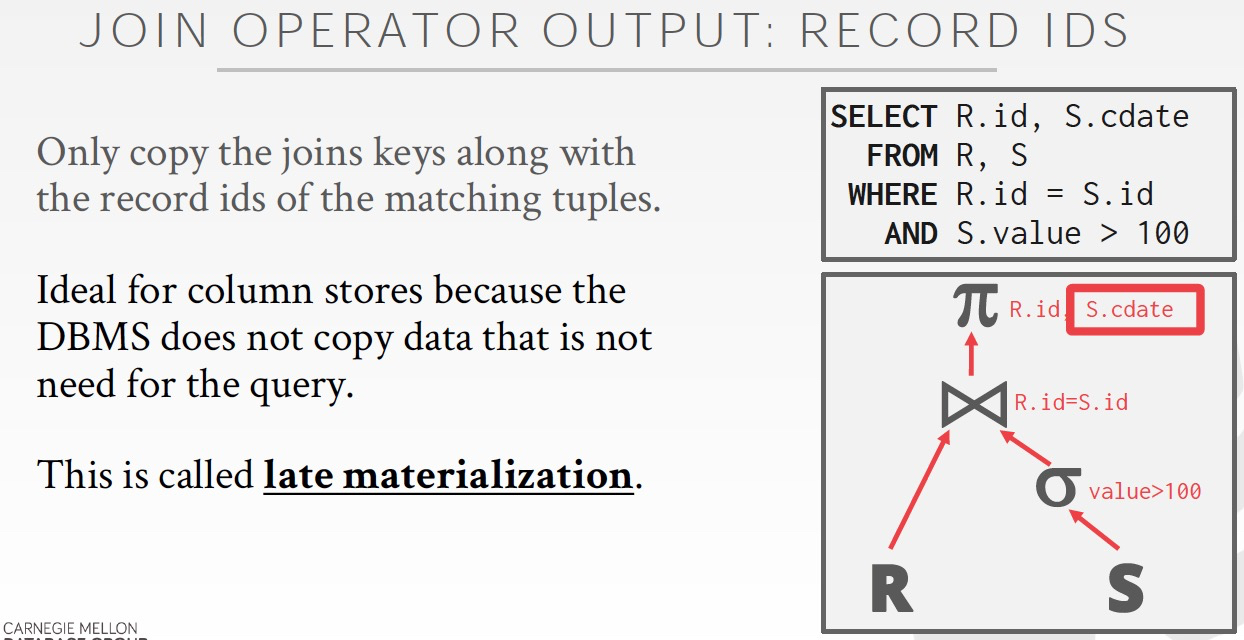
尤其适用于列存，因为这样你只需要读出join id列，也不浪费

然后在最后要显示的时候，才去把需要的数据从表里面查出来，这叫做late materialization

这样的好处，过程中可能还有其他的join，过滤等，所以开始读可能浪费，到最后真正需要的时候再读

Join Cost

如何去评价join算法的好坏，就是要评价cost

传统的数据库的瓶颈在disk IO，所以这里就以磁盘IO的次数来评价join算法的好坏，这个和为何使用B+tree作为index的理由一样
所以就是读写page的个数

Join算法

Nested Loop Join

Simple，直觉的方式就是遍历两个表
这里的概念，分为Outer和Inner表
从Cost上看，最要取决于Outer的tuples数，所以如果把较小的表N作为Outer会效率高些　　

比较明显的问题是，没有必要读那么多遍的inner表

如果我能把outer表直接放在内存中，那么只需要读一遍inner就可以了，如果不行就用如下的block的方式

如果内存大小是B，那么要用两块来放inner和output，所以可以用B-2来放outer

Cost，outer表M需要读一次，inner表需要读M/(B-2)次

这里也写了，如果memory比较大，那么cost就是M+N，只需要读一遍inner

如果有index，是否可以加快join的效率？应该可以，但是效果要看是什么index，如果hash，C=O(1)，B+tree，C=O(logn)

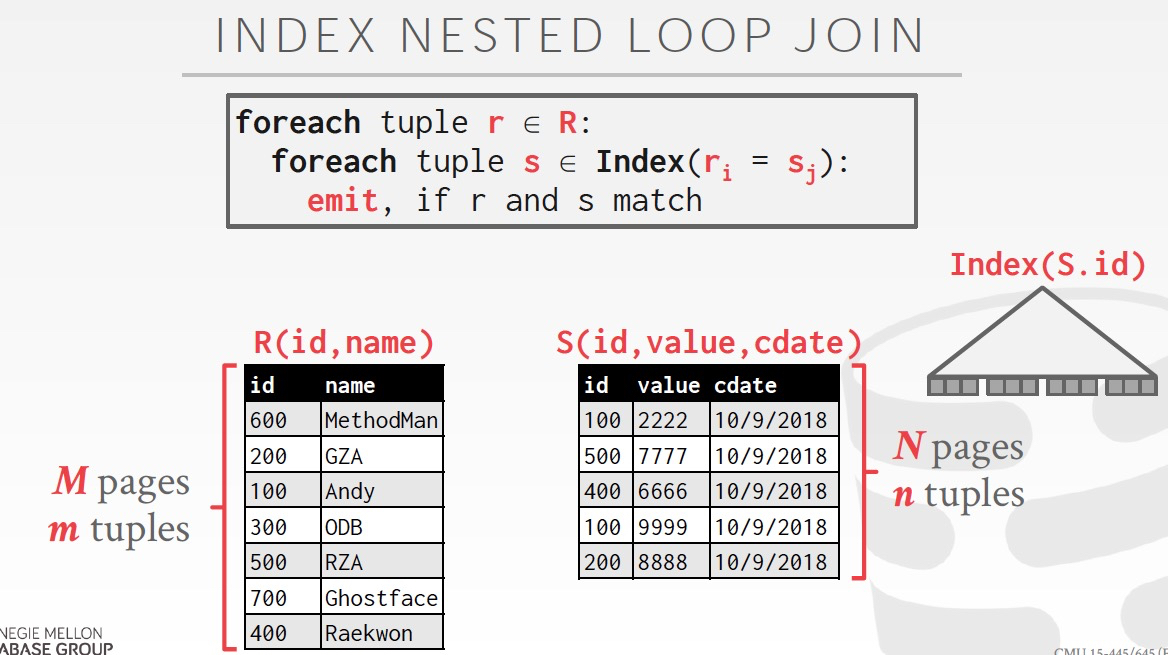
Sort-Merge Join 

这个方法要求，两个表先排序，然后做一轮幷归就可以完成join
所以这个方法适用于，两个表本身就有序，或是在join key上有index
这个方法附带的好处是结果有序

这个算法的Cost，主要是两个表排序的cost，幷归的cost就是M+N

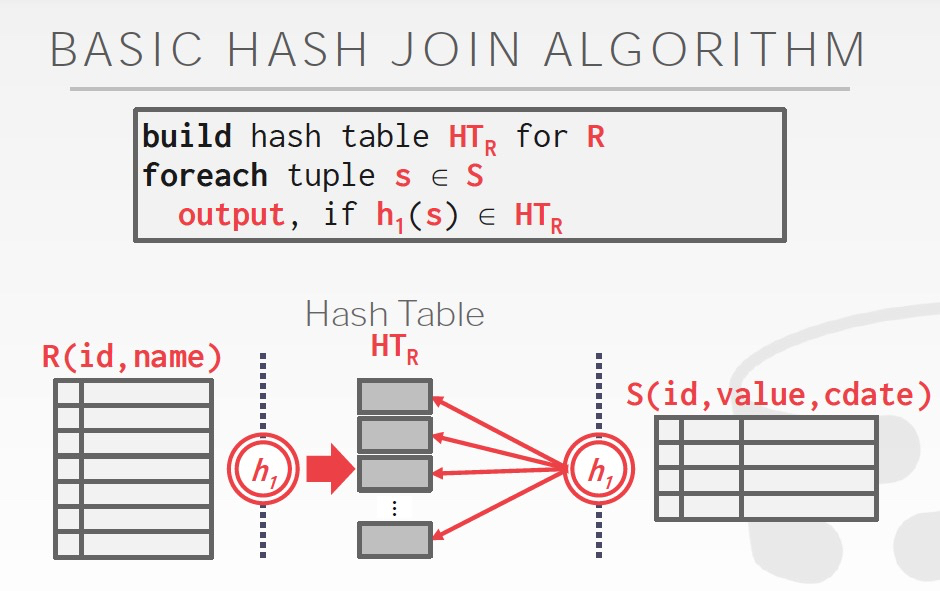
Hash Join

HashJoin分为两步，两步的hash函数用同一个

Build，对较小的表建临时的hash table

Probe，读取另一张表，进行join

这有个类似的问题，Hash Table里面存什么？

当然可以直接存join的结果，也可以存tuple id，这个选择就取决于场景

自然有个疑问，如果内存放不下这个hash table怎么办？

既然放不下，就需要分而治之，两个表用相同的hash函数，hash到相同数目的buckets里面去

在内存中，一次只读一组bucket来进行join，是不是很ok

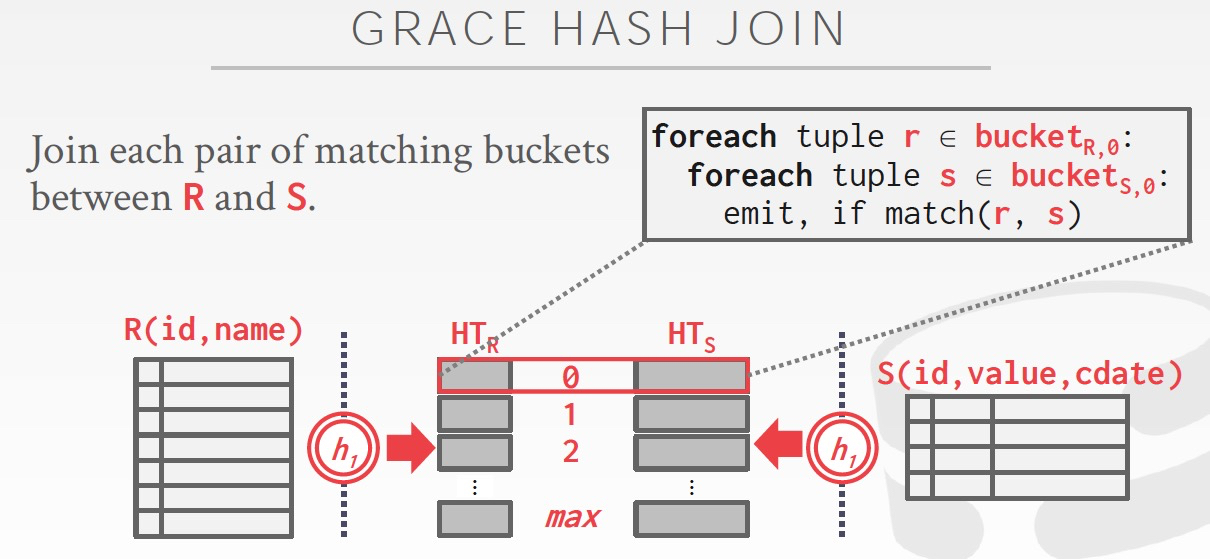
那么如果hash成bucket的时候，不均衡，一个bucket也overflow，怎么办？答案是继续分

Grace Hash Join的cost

所有join算法的Cost对比，