【CSP-S 2019】【洛谷P5665】划分【单调队列dp】

前言

\(csp\)时发现自己做过类似这道题的题目 ： P4954 [USACO09Open] Tower of Hay 干草塔

然后回忆了差不多\(15min\)才想出来。。。

然后就敲了\(88pts\)的部分分。当时的内存是\(950MB\)左右，写一个高精就炸内存了。

题目

2048 年，第三十届 CSP 认证的考场上，作为选手的小明打开了第一题。这个题的样例有 \(n\) 组数据，数据从 \(1 \sim n\) 编号，\(i\) 号数据的规模为 \(a_i\)。

小明对该题设计出了一个暴力程序，对于一组规模为 \(u\) 的数据，该程序的运行时间为 \(u^2\)。然而这个程序运行完一组规模为 \(u\) 的数据之后，它将在任何一组规模小于 \(u\) 的数据上运行错误。样例中的 \(a_i\) 不一定递增，但小明又想在不修改程序的情况下正确运行样例，于是小明决定使用一种非常原始的解决方案：将所有数据划分成若干个数据段，段内数据编号连续，接着将同一段内的数据合并成新数据，其规模等于段内原数据的规模之和，小明将让新数据的规模能够递增。

也就是说，小明需要找到一些分界点 \(1 \leq k_1 \lt k_2 \lt \cdots \lt k_p \lt n\)，使得

\[\sum_{i=1}^{k_1} a_i \leq \sum_{i=k_1+1}^{k_2} a_i \leq \cdots \leq \sum_{i=k_p+1}^{n} a_i
\]

注意 \(p\) 可以为 \(0\) 且此时 \(k_0 = 0\)，也就是小明可以将所有数据合并在一起运行。

小明希望他的程序在正确运行样例情况下，运行时间也能尽量小，也就是最小化

\[(\sum_{i=1}^{k_1} a_i)^2 + (\sum_{i=k_1+1}^{k_2} a_i)^2 + \cdots + (\sum_{i=k_p+1}^{n} a_i)^2
\]

小明觉得这个问题非常有趣，并向你请教：给定 \(n\) 和 \(a_i\)，请你求出最优划分方案下，小明的程序的最小运行时间。

思路：

假设我们现在已经划分为三个部分\(x,y,z\)满足\(x\leq y\leq z\)，那么显然是有

\[x^2+y^2+z^2<x^2+(y+z)^2
\]

所以我们肯定要做到能分就分。

但是贪心选取肯定是错误的。样例一明显就指出了错误。

考虑\(dp\)。设\(f[i]\)表示我们划分\(1\sim i\)的所有数，以\(i\)为最后一个区块的情况下，最后一个区块的最小长度。

那么枚举一个\(j\)，明显有

\[f[i]=min(\sum^{i}_{k=j}a_k)\ \ \ (\sum^{i}_{k=j}a_k\geq f[j])
\]

由于\(\sum^{i}_{k=j}a_k\)满足单调性，所以肯定选择尽量大的\(j\)来转移。

如果\(j\)可以转移到\(i\)，那么转移的同时可以求出划分的费用

\[ans[i]=ans[j-1]+(\sum^{i}_{k=j}a_k)^2
\]

这样我们就得到了一个\(O(n^2)\)的算法，可以得到\(64pts\)的高分。

我们发现，转移的条件\(\sum^{i}_{k=j}a_k\geq f[j]\)其实就是\(\sum^i_{k=1}a_k-\sum^i_{k=j}a_k\geq f[j]\)，移项就得到了\(\sum^i_{k=1}a_k\geq f[j]+\sum^i_{k=j}a_k\)

我们发现，在做了前缀和之后，上式等号左边只与\(i\)有关，等号右边只与\(j\)有关。同时我们又要满足选择尽量大的\(j\)来转移，所以就可以维护一个单调队列装\(f[j]+\sum^i_{k=j}a_k\)进行转移。

但是我们每次要选择的是满足\(\sum^i_{k=1}a_k\geq f[j]+\sum^i_{k=j}a_k\)的尽量大\(j\)进行转移，而不是单纯的最小的\(\sum^i_{k=1}a_k\geq f[j]+\sum^i_{k=j}a_k\)转移。所以我们每次要不断弹出队头，知道队头不再满足\(\sum^i_{k=1}a_k\geq f[j]+\sum^i_{k=j}a_k\)。此时将最后一次弹出的元素再从头部插入进行转移。这样就保证了每次选择\(j\)最大的满足条件的元素进行转移。容易证明，弹出的元素不会对后面的转移产生影响。

这样每个元素最多进入队列1次，时间复杂度\(O(n)\)。

这样我们就得到了\(88pts\)的高分。

对于\(type=1\)的数据点需要使用高精，但是由于\(O(n)\)的算法我们的内存已经使用了\(950MB\)，所以几乎没有空间来敲高精。

所以此时就只能用csp不允许使用的__int128了

我们将\(ans\)改为\(\_\_int128\)类型，是可以存下最终答案的。

然后我就愉快的T了。



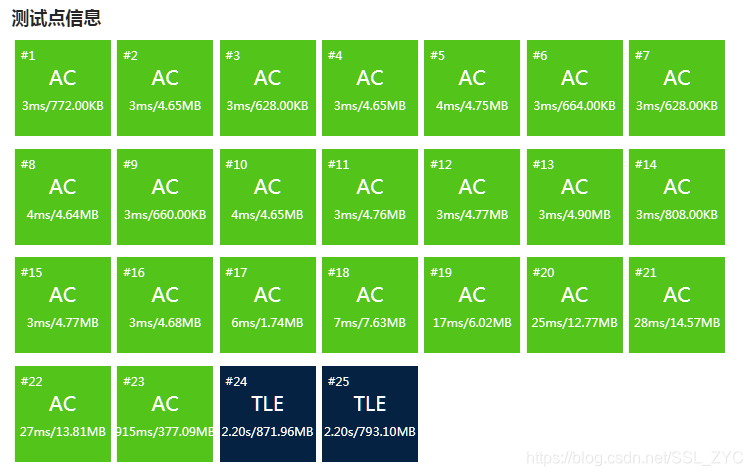
在尝试过所有我知道的化学性卡常后，样例三依然需要\(2.4s+\)才可以跑过。

所以此时就只能用csp不允许使用的Ofast了

物理性卡常\(nb\)！样例最终可以在\(0.85s\)左右跑过。

然后我就愉快的MLE了。



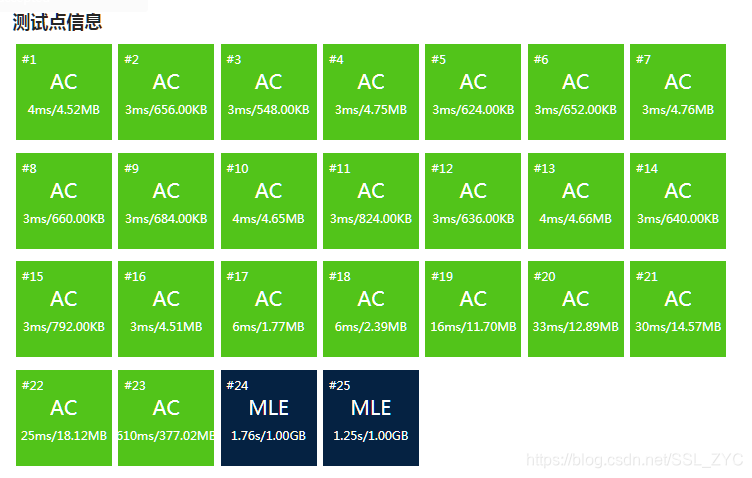
经过输出后，\(ans,f,sum\)三个数组加起来是\(1200+MB\)。将近\(200MB\)的差距，只能考虑删除一个数组了。

\(ans\)和\(sum\)是肯定无法删除的，而\(f\)我们发现，在转移时是等于\(sum[i]-sum[last]\)的，其中\(last\)直可以转移的最大的\(j\)。

所以我们考虑直接用\(sum\)数组来表示出\(f\)数组。这样我们往单调队列插入时就要插入\(i,f_i+sum_i\)两维，因为后者在去掉\(f\)数组后是没办法算出来的。

最终还是以\(1.38s,804.98MB\)过了这道题。但是在\(csp\)时是不允许用\(\_\_int128\)和\(Ofast\)的，所以其实这份代码无论是时间还是空间都是过不去的

代码：

#pragma GCC optimize("Ofast")
#pragma GCC optimize("inline")
#include <queue>
#include <cstdio>
#include <string>
#include <cstring>
#include <algorithm>
#define mp make_pair
using namespace std;
typedef long long ll;

const int N=40000010,MOD=(1<<30),M=100010;
int n,x,type,cnt,id;
ll d,xx,yy,zz,m,sum[N],b[4],p[M],l[M],r[M];
__int128 ans[N];
pair<int,ll> last;
char ch;
deque<pair<int,ll> > q;

inline ll read()
{
	d=0; ch=getchar();
	while (!isdigit(ch)) ch=getchar();
	while (isdigit(ch))
		d=(d<<3)+(d<<1)+ch-48,ch=getchar();
	return d;
}

inline void write(__int128 x)
{
	if (x>9) write(x/10);
	putchar(x%10+48);
}

inline ll Get(int i)
{
	int id=(i-1)%3+1;
	if (i>2 && id==1) b[1]=(xx*b[3]+yy*b[2]+zz)%MOD;
	if (i>2 && id==2) b[2]=(xx*b[1]+yy*b[3]+zz)%MOD;
	if (i>2 && id==3) b[3]=(xx*b[2]+yy*b[1]+zz)%MOD;  //减少模运算次数
	if (i>p[cnt]) cnt++;
	return (b[id]%(r[cnt]-l[cnt]+1))+l[cnt];
}

int main()
{
	scanf("%d%d",&n,&type);
	if (type)
	{
		xx=read(); yy=read(); zz=read(); b[1]=read(); b[2]=read(); m=read();
		for (int i=1;i<=m;i++)
			p[i]=read(),l[i]=read(),r[i]=read();
	}
	q.push_back(mp(0,0));
	for (register int i=1;i<=n;i++)
	{
		sum[i]=sum[i-1]+(type?Get(i):read());
		while (q.size() && sum[i]>=q.front().second)
		{
			last=q.front();
			q.pop_front();
		}
		q.push_front(last);
		int pos=last.first;
		ans[i]=ans[pos]+(__int128)(sum[i]-sum[pos])*(sum[i]-sum[pos]);
		while (q.size() && q.back().second>=sum[i]-sum[pos]+sum[i]) q.pop_back();
		q.push_back(mp(i,sum[i]-sum[pos]+sum[i]));
	}
	write(ans[n]);
	return 0;
}