AtCoder-arc059 (题解)

A - いっしょ / Be Together (结论/暴力)

题目大意：

有 $n$ 个数字，要将它们变成相等，对每一个数字最多操作一次，如将 $a \to b$ 的代价为 $(a-b)^2$ ，求出最小的代价。

大致思路：

根据不等式的知识可以知道，假设最后数字变为 $x$，那么 $x$ 为 $\sum{a_i}$ 平均数的代价最小，由于要为整数，就取最接近 $x$ 两个整数做为结果，取其中最小的代价就行了。

代码：

#include<bits/stdc++.h>

using namespace std;

int n;

int a[200];

int main()

{

	//freopen("H:\\c++1\\in.txt","r",stdin);

	//freopen("H:\\c++1\\out.txt","w",stdout);

	scanf("%d",&n);

	int ans1=0,ans2=0,sum=0;

	for(int i=1;i<=n;i++){

		scanf("%d",&a[i]);

		sum+=a[i];

	}

	int t1=sum/n,t2=(sum+n-1)/n;

	for(int i=1;i<=n;i++){

		ans1+=(t1-a[i])*(t1-a[i]);

		ans2+=(t2-a[i])*(t2-a[i]);

	}

	printf("%d\n",min(ans1,ans2));

	return 0;

}

B - アンバランス / Unbalanced (思维)

题目链接

题目大意：

给定一个字符串 $s$ ，问其中是否存在“不平衡”的连续子串，“不平衡”的字符串被定义为长度大于等于 $2$ ，且其中一个字母出现次数过半。有的话任意输出一个。

大致思路：

一开始，想到要大于半数，那么必须存在两个相邻的字母相同，交上去 $wa$ 了，后来发现其实还有一种可能就是 $3$ 个字母，头尾相同，如 $aba$ ，把两种情况都枚举一下，就行了。

代码：

#include<bits/stdc++.h>

using namespace std;

const int N=1e5+10;

char s[N];

int main()

{

	//freopen("H:\\c++1\\in.txt","r",stdin);

	//freopen("H:\\c++1\\out.txt","w",stdout);

	scanf("%s",s+1);

	int len=strlen(s+1);

	if(len==2&&s[1]==s[2]){ // 特判

		printf("1 2\n");

		return 0;

	}

	int l=-1,r=-1;

	for(int i=1;i<len-1;i++){

		if(s[i]==s[i+1]||s[i]==s[i+2]||s[i+1]==s[i+2]){

			l=i,r=i+2;

			break;

		}

	}

	printf("%d %d\n",l,r);

	return 0;

}

C - キャンディーとN人の子供 / Children and Candie (dp+计算贡献)

题目链接

题目大意：

有 $n$ 个人， $C$ 个糖果，将 $C$ 个糖果分配给 $n$ 个人,每一个人有 $c_i$ 个，可以为 $0$ 个，每一个人有一个活跃度 $x_i$ ，那么这次分配的价值为 $\prod{x_i^{c_i}}$ ，将所有可能的分配的价值和用 $f(x_1,x_2,...,x_n)$ 表示，现在给你两个数字 $A[n],B[n]$ ,要求求出下式。

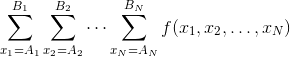
大致思路：

虽然这题过了，但是还是有很多细节的部分没用弄懂，一开始根本没有想到 $dp$ 来解，后来看了题解才知道，当 $A_i=B_i$ 的情形比较好想，设 $dp[i] [j]$ 表示分给前i个人，使用 $j$ 个糖果的价值数，那么可以写出方程，$dp[i][j]+=dp[i-1][j-k]*(A_i^k)$ ， $k$ 其实就是枚举分给第 $i$ 个人的糖果，但是当 $A_i != B_i$ 的时候，我对于为什么可以将求和号提出来有些疑惑，就是为什么可以单独计算某一个对总体的贡献。具体的解法就是，将上述方程改成 $dp[i] [j] += dp[i-1] [j-k] * (\sum_{t=A[i]}^{B[i]}{t^k})$，然后通过预处理就可以 $O(n^3)$ 的过了。

(之后还得在思考思考)

代码:

#include<bits/stdc++.h>

#define ll long long

using namespace std;

const int N=500;

const int mod=1e9+7;

ll ksm(ll a,ll b){ // 快速幂

	ll res=1,t=a;

	while(b){

		if(b&1)res=(res*t)%mod;

		t=(t*t)%mod;

		b>>=1;

	}

	return res;

}

ll dp[N][N];

ll n,c;

ll a[N],b[N];

ll p[N][N];

ll sum[N][N];

void init(){ // 预处理

	for(int i=1;i<N;i++)

	for(int j=0;j<N;j++)p[i][j]=ksm(i,j);

	for(int k=0;k<N;k++){

		for(int i=1;i<N;i++)sum[i][k]=(sum[i-1][k]+p[i][k])%mod;

	}

}

int main()

{

	//freopen("H:\\c++1\\in.txt","r",stdin);

	//freopen("H:\\c++1\\out.txt","w",stdout);

	init();

	scanf("%lld%lld",&n,&c);

	for(int i=1;i<=n;i++)scanf("%lld",&a[i]);

	for(int i=1;i<=n;i++)scanf("%lld",&b[i]);

	dp[0][0]=1;

	for(int i=1;i<=n;i++)

	for(int j=0;j<=c;j++){

		for(int k=0;k<=j;k++){ //枚举第i个人拿的糖果数

			dp[i][j]=(dp[i][j]+(dp[i-1][j-k]*(sum[b[i]][k]-sum[a[i]-1][k]+mod)%mod))%mod;

		}

	}

	printf("%lld\n",dp[n][c]);

	return 0;

}

D - バイナリハック / Unhappy Hacking (dp计数)

题目链接

题目大意：

有 $3$ 个按键，分别是 $，，0，1，backspace$ 键，按下 $0$ 或者 $1$ ，就会在最右边出现 $0$ 或者 $1$ ，按下 $backspace$ 键就会将最右边的数字删去，如果没有数字就无事发生。现在告诉你一串数字，并且按了 $n$ 次键，问有几种按法。

大致思路：

这题一开始想分类讨论，后来发现删除的数字若是连在一起又可以改变删除的顺序就不会做了，看了题解，原来就是我一开始写的 $dp$ ，但是当时不懂怎么转移。用 $dp[i][j]$ 表示按了 $i$ 下，数字长度为 $j$ 的方案数，我们考虑当前按下的是数字，那么必然是和给定串的对应位相同，若按下的是删除键，那么就这位删除的可以是 $0$ 也可以是 $1$ 就有两种可能，按照这个转移一下即可。

代码：

#include<bits/stdc++.h>

#define ll long long

using namespace std;

const int N=5010;

const int mod=1e9+7;

ll dp[N][N];

char s[N];

int n;

int main()

{

	//freopen("H:\\c++1\\in.txt","r",stdin);

	//freopen("H:\\c++1\\out.txt","w",stdout);

	dp[0][0]=1;

	scanf("%d",&n);

	scanf("%s",s+1);

	int len=strlen(s+1);

	for(int i=0;i<=n;i++)

	for(int j=0;j<=n;j++){

		if(j==0)dp[i+1][j]=(dp[i][j]+dp[i+1][j])%mod;//特判

		else{

			dp[i+1][j-1]=(dp[i][j]*2+dp[i+1][j-1])%mod;//按backspace

		}

		dp[i+1][j+1]=(dp[i+1][j+1]+dp[i][j])%mod;//按数字键

	}

	printf("%lld\n",dp[n][len]);

	return 0;

}