[清华集训2015]灯泡(浙江大学ZOJ 3203 Light Bulb）

Time Limit: 1 Second      Memory Limit: 32768 KB

Compared to wildleopard's wealthiness, his brother mildleopard is rather poor. His house is narrow and he has only one light bulb in his house. Every night, he is wandering in his incommodious house, thinking of how to earn more money. One day, he found that the length of his shadow was changing from time to time while walking between the light bulb and the wall of his house. A sudden thought ran through his mind and he wanted to know the maximum length of his shadow.

Input

The first line of the input contains an integer T (T <= 100), indicating the number of cases.

Each test case contains three real numbers H, h and D in one line. H is the height of the light bulb while h is the height of mildleopard. D is distance between the light bulb and the wall. All numbers are in range from 10^-2 to 10³, both inclusive, and H - h >= 10^-2.

Output

For each test case, output the maximum length of mildleopard's shadow in one line, accurate up to three decimal places..

Sample Input

3
2 1 0.5
2 0.5 3
4 3 4

Sample Output

1.000
0.750
4.000

题目链接

题目大意：

他的房子狭窄，他家里只有一个灯泡。每天晚上，他都在他不知名的房子里徘徊，想着如何赚更多的钱。有一天，他发现他的影子长度在灯泡和房子的墙壁之间行走时不时变化。突然想到了他的思绪，他想知道他的影子的最大长度。

输入的第一行包含整数T（T <= 100），表示个案数。

每个测试用例在一行中 包含三个实数H，h和D. H是灯泡的高度，而h是轻度高度的高度。 D是灯泡和墙壁之间的距离。所有数字的范围均为10 ^-2至10 ³，包括两者，H - h > = 10 ^-2。

对于每个测试用例，在一行中输出mildleopard阴影的最大长度，精确到三位小数。

算法分析

参考：

https://blog.csdn.net/Mrx_Nh/article/details/52745348    分析理解应该是对的，但是代码有误，估计是没有讨论影子不落到墙上的情况。

https://blog.csdn.net/qq_38944163/article/details/80870928  代码是正确的。

这个题要分两种情况讨论：影子没有落到墙上；影子落到墙上。

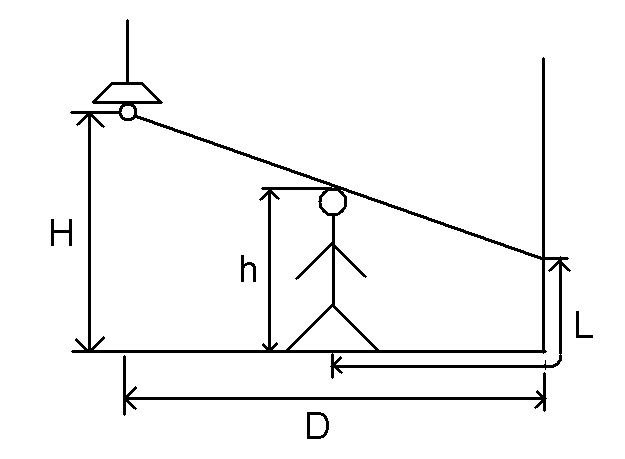
影子没有落到墙上的情况如下图所示：

影子落到墙上的情况如下图所示

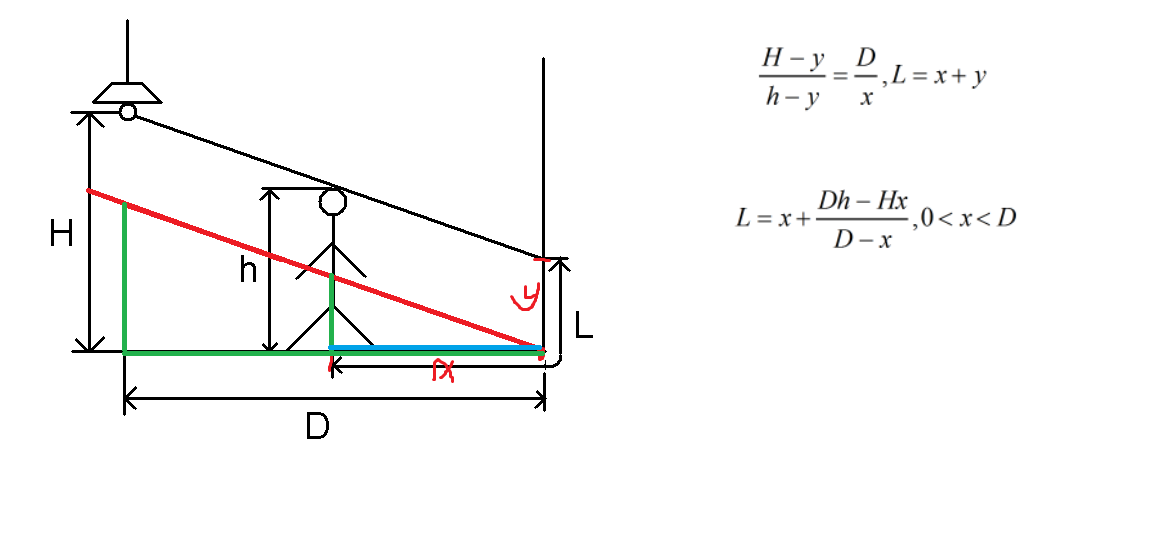
算影子的长度可以用相似三角形，相信各位上过初中的朋友都会。。

那么我们发现这是一个单峰函数，要求峰值，这里我们可以用一个很强大的东西，三分法。

具体看代码吧

 #include<stdio.h>
 double f(double x,double H,double h,double D)
 {
     double tanA,Y;
     tanA=(H-h)/x;//这里大家可以画个图帮助理解
     Y=H/tanA;//下面那条的长（在没有墙的情况下）
     if(Y<=D) return Y-x;//如果没到墙，就直接返回地上影子的长度。
     Y=Y-D;
     return D-x+Y*tanA;//D-X是地上影子的长度,Y*tanA是墙上影子的长度.
 }
 int main()
 {
     freopen("p3382.in","r",stdin);
     int i,T;
     double H,h,D;
     double L,R,m1,m2,fm1,fm2;
     scanf("%d",&T);
     for(i=;i<T;i++)
     {
         scanf("%lf%lf%lf",&H,&h,&D);
         L=;R=D;
         while(L+1e-<R)
         {
             m1=L+(R-L)/; m2=R-(R-L)/;
             fm1=f(m1,H,h,D);  fm2=f(m2,H,h,D);
             if(fm1<fm2) L=m1;
             else R=m2;
         }
         printf("%.3lf\n",f(L,H,h,D));
     }
     return ;
 }

为何是一个单峰，可以考虑看一下第一个参考的博客。

理解时参考下图：