作业:IEEE754浮点数
人工转换:
5.75转换成二进制:101.11右移2位,补0:1.0111000000000000000000000000000000000000000000000000.10000000001
161.875转换:10100001.111右移6位,补0:1.010000111100000000000000000000000000000000000000000.10000000110
-0.0234375转换:0.0000011左移6位,补0:1.100000000000000000000000000000000000000000000000000.的11位补码,即为00000000110----->01111111001为1.100000000000000000000000000000000000000000000000000.01111111001
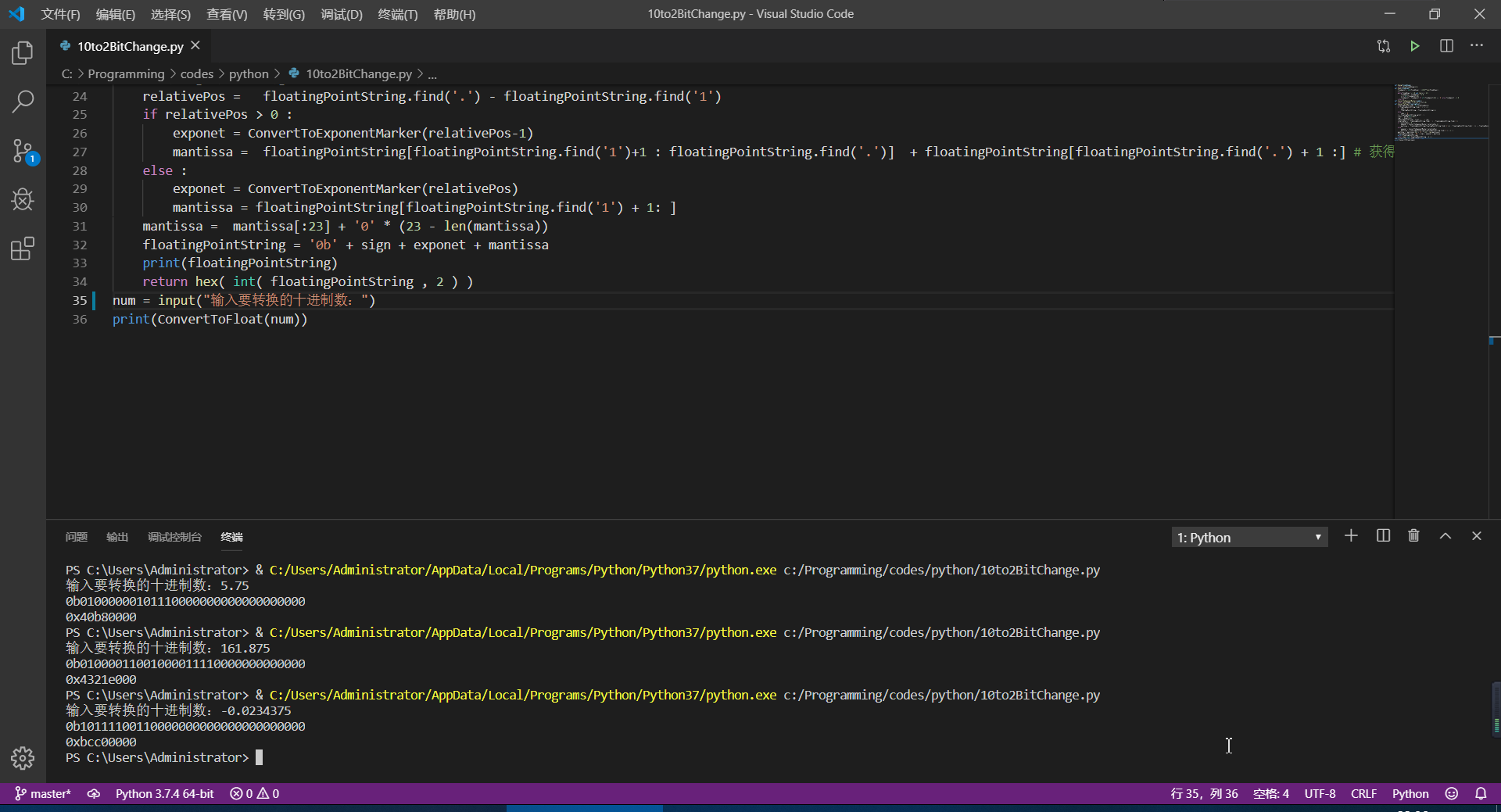
用python实现:
-参照网上的办法,虽然通过打代码实现了,但是我的python水平实在有限,未能理解一些定义的函数的意义。但是我基本上可以理解转换的原理,可以手动转换成功。
代码链接
作业:IEEE754浮点数的更多相关文章
- 震惊!计算机连0.3+0.6都算不对?浅谈IEEE754浮点数算数标准
>>> 0.3+0.6 0.8999999999999999 >>> 1-0.9 0.09999999999999998 >>> 0.1+0.1+ ...
- 把一个IEEE754浮点数转换为IBM370浮点数的C#代码
把一个IEEE754浮点数转换为IBM370浮点数的C#代码. 在这个网页上有古老的IBM370浮点格式的说明. // http://en.wikipedia.org/wiki/IBM_Floatin ...
- IEEE754 浮点数
IEEE754 浮点数 1.阅读IEEE754浮点数 A,阶码是用移码表示的,这里会有一个127的偏移量,它的127相当于0,小于127时为负,大于127时为正,比如:10000001表示指数为129 ...
- IEEE754浮点数
前言 Go语言之父Rob Pike大神曾吐槽:不能掌握正则表达式或浮点数就不配当码农! You should not be permitted to write production code if ...
- IEEE754浮点数表示法
IEEE二进制浮点数算术标准(ANSI/IEEE Std 754-1985)是一套规定如何用二进制表示浮点数的标准.就像"补码规则"建立了二进制位和正负数的一一对应关系一样,IEE ...
- IEEE Floating Point Standard (IEEE754浮点数表示法标准)
浮点数与定点数表示法是我们在计算机中常用的表示方法 所以必须要弄懂原理,特别是在FPGA里面,由于FPGA不能像在MCU一样直接用乘除法. 定点数 首先说一下简单的定点数,定点数是克服整数表示法不能表 ...
- matlab中实现 IEEE754浮点数 与 一般十进制数之间 互相转换的方法
------------恢复内容开始------------ %2020/12/2 11:42:31clcformat long % IEEE754 to deca = '40800000'a = d ...
- IEEE754浮点数的转换
将十进制数转换为单精度浮点数 如何将十进制数转换为单精度浮点数参考 首先要知道 IEEE浮点标准:V=(-1)^s * M * 2^E 1.符号(sign)s决定这个数是负数(s=1)还是正数,0(s ...
- IEEE754浮点数的表示方法
https://blog.csdn.net/K346K346/article/details/50487127
随机推荐
- MAC OS系统替换brew.npm, pip 使用阿里云的镜像源
替换brew.git:cd "$(brew --repo)"git remote set-url origin https://mirrors.aliyun.com/homebre ...
- expor和import的用法
1.Export 模块是独立的文件,该文件内部的所有的变量外部都无法获取.如果希望获取某个变量,必须通过export输出 // profile.js export var firstName = 'M ...
- Springboot生成二维码并下载图片png支持打包成zip
pom.xml <!--二维码--> <dependency> <groupId>com.google.zxing</groupId> <arti ...
- 2007英语CET6四6级资料六级大学单词
anticipation n. 预期,期望 appreciation n. 感谢,感激 array n. 陈列,一系列 assurance n. 保证 emergency n. 紧急情况 encour ...
- android studio打印
写入打印语句 System.out.println("hello furong"); 添加打印过滤 指定过滤规则 Filter Name:随便写 Log Tag:日志标志 Log ...
- LP线性规划初识
认识LP 线性规划(Linear Programming) 特指目标函数和约束条件皆为线性的最优化问题. 目标函数: 多个变量形成的函数 约束条件: 由多个等式/不等式形成的约束条件 线性规划: 在线 ...
- Golang: 读取文件并统计内容
上次我们从命令行接收用户输入,并统计了每次输入内容出现的次数,今天对程序加以改造,使其能够读取文件内容,并统计每行文本出现的次数. 首先,我们把接收输入的逻辑封装成一个函数: // scan.go p ...
- Linux服务器相关信息查询
链接:https://www.cnblogs.com/luoahong/articles/8781375.html 机器型号dmidecode | grep "Product Name&qu ...
- k8s之StatefulSet介绍(六)
复制有状态的Pod replicaSet通过一个pod模版创建多个pod副本.这些副本除了它们的名字和IP地址不同外,没有别的差异.如果pod模版里描述了一个关联到特定持久卷声明的数据卷,那么Repl ...
- Spring Cloud 手记
文档:https://www.springcloud.cc/spring-cloud-dalston.html#_features 一年了,我们都用 Spring Cloud 干了啥?:https:/ ...
