Joint Approximative Diagonalization of Eigen matrix (JADE)

特征矩阵联合相似对角化算法[1]。

Cardoso于1993年提出的盲信号分离具有代表性的一种算法。是一种基于四阶累积量特征矩阵近似联合对角化盲分离算法。该算法将目标函数最大化问题等价于一组四阶累积量矩阵的特征矩阵的联合对角化问题，不仅大大简化了算法的计算复杂度，同时还有效提高了算法的分离性能。

原理

JADE算法原理就是将白化后的混合信号的四阶累积量矩阵(或二阶相关矩阵)通过U变换，压缩为一个对角矩阵，从而求解酉矩阵U。

白化

信号模型如式x(t) = As(t)所示，源信号之间相互统计独立。由于盲分离问题中，源信号的真实幅度不可解，为方便算法研究，一般通过去均值化等数学方法将各个源信号分量转化为零均值且方差为1的随机变量。白化数据是JADE算法的第一步，通过白化可以恢复信号之间的二阶独立性。对观测信号的相关矩阵进行特征分解：

白化矩阵：

白化信号有：

显然，矩阵 V 为正交矩阵。JADE 算法的目的就是寻找一个正交矩阵U = VJP ，使源信号分离：

其中 P为置换矩阵，J 为对角矩阵。

对照函数

根据四阶累积量的平方和性质易知，对照函数式（2.8）的最大化等价于除c(U) 所包含的四阶累积量之外的所有互累积量平方和的最小化，因此可以实现信号分离。然而对照函数的计算非常复杂，难以实用化。但所幸的是 Cardoso 证明，它与一组矩阵的联合对角化等价，而且这组矩阵包含了所有四阶累积量，因而不但减少了算法的运算量，同时还提高了算法的分离性能。

JADE

给定一个矩阵集合N={Nr|1≤r≤s}，一个酉矩阵U对其联合对角化等价于下面目标函数的最大化：

一般情况下，矩阵集合N不能同时完全被酉矩阵U联合对角化，只能近似对角化，因此称之为联合近似对角化。定义矩阵集合：

Cardoso等人已证明，对于这个矩阵集存在如下等式：

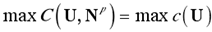
则对照函数最大化问题转化成了一组矩阵的联合近似对角化问题。为进一步简化算法，Cardoso等已证明可将四阶累积量矩阵用特征矩阵表示。对于任一给定矩阵，定义矩阵，

对于任意的K维具有四阶累积量的随机矢量z，存在K²个实数和N²个N×N阶特征矩阵Mi满足下式：

利用随机矢量z(t)的所有四阶累积量构造K²×K²矩阵Cz，对Cz作特征值分解即可得到特征值及特征矩阵（由N²维的特征向量反堆栈为N×N特征矩阵），将特征值按由大到小的顺序排列，取前K个特征值及对应的特征矩阵组成累积量特征矩阵集合，对这组矩阵进行近似联合对角化就可求得酉矩阵U，进而实现源信号的分离。

参考文献

[1] Cardoso J F, Souloumiac A. Blind Beamforming for non Gaussian Signals[J]. IEE Proc.-F, 1993, 140(6):362-370.

[2] 熊坤来. 盲分离及其在阵列信号处理中的应用研究[D]. 国防科学技术大学, 2015.