[IOI2008/BZOJ1791 岛屿]（处理基环树的小技巧&基于bfs树形DP）

IOI2008/BZOJ1791 岛屿

题目大意是在一个基环树森林里求每一棵基环树的直径①的和。

其实就是树的直径的基环树升级版。我们先把环找出来，然后从环上的每一个节点x出发，并且不经过环上其他节点，做一次树形DP，求出x的子树中到x最远的路径长d[x]和x的子树的直径dp[x]。

那么基环树的直径只有两种情况：

1.直径不经过环上的节点

　　对于每一个dp[x]取max就好了。

2.直径经过环上的节点

　　对于任意环上的两个节点x和y，都可以构成一条路径d[x]+d[y]+dist(x,y)，其中dist(x,y)为x和y在环上的距离②。

　　可以直接n^2枚举找最大的吗?当然不能，N<=1e6耶。

　　这个时候就要用一点套路。首先把环复制一遍接在原先的环后，然后对dist数组做个前缀和s，那么一条路径就成了(x>y) d[x]+d[y]+s[x]-s[y]=(d[x]+s[x])+(d[y]-s[y])，也就是说对于每个x我们需要找到在x之前的一个y满足(d[y]-s[y])最大，并且x-y<=环长。单调队列优化的套路嘛！

①基环树的直径：即基环树中最长的简单路径，这里简单路径指的是不自交（不重复经过任何点或边）的路径。

②环上的距离：有顺时针和逆时针两种，因为求的是直径，所以取两者中较长的。

这是luogu的AC代码：（温馨提示：代码太丑并且不是重点，您大可直接跳过看后面）

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+;
typedef long long LL;
struct edge{
    int v,w,last;
}e[N<<];
int tot=,tail[N];
inline void add(int x,int y,int z){
    e[++tot]=(edge){y,z,tail[x]};
    tail[x]=tot;
}
inline int read(){
    int x=,w=;char ch=;
    while(!isdigit(ch)) w|=ch=='-',ch=getchar();
    while(isdigit(ch)) x=(x<<)+(x<<)+(ch^),ch=getchar();
    return w?-x:x;
}
bool incur[N];
int n,dn,cnt,dfn[N],tp,st[N][],c[N],s[N];
void getcur(int x,int pre){
    dfn[x]=++dn;
    for(int p=tail[x];p;p=e[p].last)if(p^pre^){
        int &v=e[p].v,&w=e[p].w;
        if(dfn[v]){
            if(dfn[v]>=dfn[x]) continue;
            c[cnt=]=v,s[cnt]=w,incur[v]=true;
            for(int i=tp;st[i][]^v;--i) c[++cnt]=st[i][],s[cnt]=st[i][],incur[st[i][]]=true;
        }
        else st[++tp][]=v,st[tp][]=w,getcur(v,p);
    }
    --tp;
}

int hd,rt,tl,q[N<<];
LL ans,t,d[N],f[N],dp[N],sum[N<<];
LL dfs(int x,int pre){
    LL t=;d[x]=f[x]=;
    for(int p=tail[x];p;p=e[p].last)if(p^pre^){
        int &v=e[p].v,&w=e[p].w;
        if(incur[v]||v==pre) continue;
        t=max(t,dfs(v,x)),f[x]=max(f[x],d[x]+d[v]+w),d[x]=max(d[x],d[v]+w);
    }
    return max(f[x],t);
}
LL F(int id){
    return dp[id]-sum[id];
}
int main(){
    n=read();
    for(int i=;i<=n;++i){
        int x=read(),y=read();
        add(x,i,y),add(i,x,y);
    }
    for(int i=;i<=n;++i)if(!dfn[i]){
        memset(sum,,sizeof sum);
        st[tp=][]=i,st[tp][]=;
        cnt=;getcur(i,);
        t=;
        for(int j=;j<=cnt;++j) t=max(t,dfs(c[j],)),dp[j]=dp[j+cnt]=d[c[j]];
        int hd=tl=;
        for(int j=;j<=cnt*;++j){
            sum[j]+=sum[j-]+s[(j-)>cnt?j--cnt:j-];
            while((hd^tl)&&j-q[hd]+>cnt) ++hd;
            if(hd^tl) t=max(t,F(q[hd])+dp[j]+sum[j]) ;
            while((hd^tl)&&F(j)>F(q[tl-])) --tl;
            q[tl++]=j;
        }
       ans+=t;
    }
    cout<<ans<<endl;
    return ;
}

又是找环，又是树形DP，又是单调队列优化的，是不是很恶心？没错，虽然用的算法不算高级，但由于种种原因做此题的人各种RE&WA&MLE&TLE，因此在洛谷上都成黑题了。

并且我要告诉你更恶心的是，由于BZOJ栈的限制，上面这份dfs的代码在BZOJ上还会爆栈......

正是在这种山穷水尽的时候，我发现了一些黑科技。

首先我们要分析题目图的特性，这是一棵无向基环树（暂时不管森林），画出来应该是这个样子（没画边权，下同）：

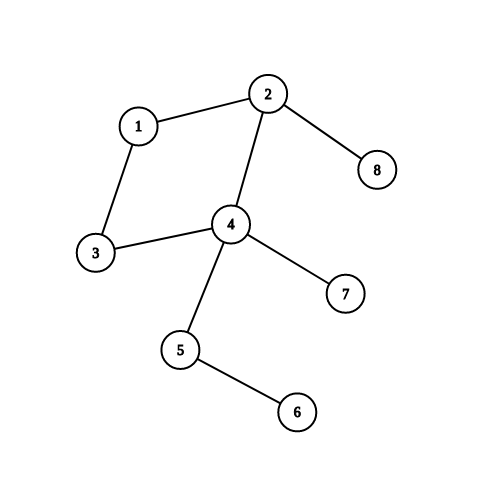
题目的输入方式有点特别，是第i+1行输入一个x和y表示i+1和x有一条长度为y的边。那么我们暂时把它当作有向边，令to[i+1]=x,w[i+1]=y，画出来就是这个样子：

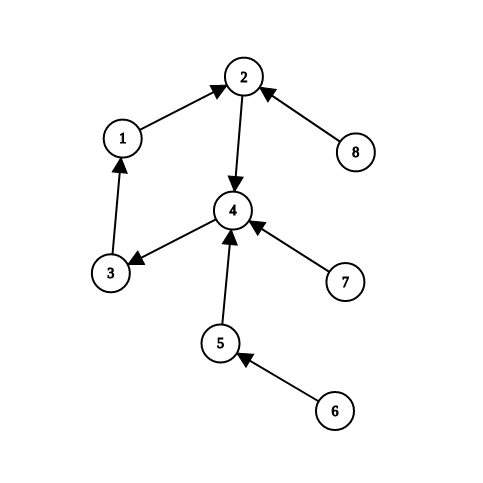
它刚好是一棵内向树③！这是巧合吗？不是的。按照这种输入方式，每个点有且仅有一条出边，连出来就一定是一棵内向树。这样一来，我们就得到了每个节点x的父亲f[x]与它到父亲的边权w[x]，当然对于环上的节点是到它相邻节点的，且一定是同一个方向（有点不太好表达，看代码就懂了）。于是我们就可以用按拓扑排序的顺序自底向上地DP了，也就是基于bfs的树形DP。代码：

③内向树：n个点，n条边，每个节点有且仅有一条出边的有向连通图就好像以”基环“为中心，有向内收缩的趋势，故称为”内向树“。

#include<bits/stdc++.h>
using namespace std;
#define rg register
const int N=1e6,M=1e6+;
typedef long long LL;
inline int read(){
    int x=,w=;char ch=;
    while(ch<''||ch>'') w|=ch=='-',ch=getchar();
    while(ch>=''&&ch<='') x=(x<<)+(x<<)+(ch^),ch=getchar();
    return w?-x:x;
}
bool v[M];
int n,cnt,dcnt,cur[M<<],to[M],w[M],in[M];
LL t,ans,s[M<<],d[M],f[M],dp[M];
struct Deque{//这个。。。手写的双端队列，不用管它
    int l,r,q[N];
    Deque(){l=r=;}
    void clear(){l=r=;}
    bool empty() {return !(l^r);}
    void push_back(int v) {q[r++]=v;r%=N;}
    void push_front(int v) {q[l=(l-+N)%N]=v;}
    void pop_front() {++l;l%=N;}
    void pop_back() {r=(r-+N)%N;}
    int front() {return q[l];}
    int back() {return q[r-];}
}q;
int main(){
    n=read();
    for(rg int i=;i<=n;++i) ++in[to[i]=read()],w[i]=read();
    for(rg int i=;i<=n;++i) if(!in[i]) q.push_back(i);//入度为0的点入队
    while(!q.empty()){
        int x=q.front(),&fa=to[x],&l=w[x];q.pop_front();
        if(!--in[fa]) q.push_back(fa);
        //下面3行是DP，也就是更新父节点的信息
        f[fa]=max(f[fa],d[fa]+d[x]+l); //f：x的子树中经过x节点的最长路径
        d[fa]=max(d[fa],d[x]+l);//d: x的子树中离x最远的节点到x的距离
        dp[fa]=max(dp[fa],max(dp[x],f[fa])); //dp：x的子树的直径，也就是对f[x]和dp[y](to[y]=x)取max
    }
    for(rg int i=;i<=n;++i)if(in[i]&&!v[i]){//基环树森林，不只一个环，用v标记
        cnt=;t=;
        for(rg int j=i;!v[j];j=to[j]){//这就是上面说的，这样一直沿着to走，一定能绕环一圈
            cur[++cnt]=j,v[j]=true;//把环抠下来
            t=max(t,dp[j]);//上面讨论的基环树直径的第一种情况
        }
        dcnt=cnt<<;
        for(int i=cnt+;i<=dcnt;++i) cur[i]=cur[i-cnt];//复制一遍环
        q.clear();//注意清空
        for(rg int j=;j<=dcnt;++j){
            s[j]=s[j-]+w[cur[j-]];//前缀和
            while(!q.empty()&&j-q.front()>=cnt) q.pop_front();//使满足j-q.front()+1<=cnt
            if(!q.empty())
                t=max(t,d[cur[q.front()]]-s[q.front()]+d[cur[j]]+s[j]);
            while(!q.empty()&&d[cur[j]]-s[j]>d[cur[q.back()]]-s[q.back()]) q.pop_back();
            q.push_back(j);
        }
        ans+=t;//累加每一棵基环树的直径
    }
    printf("%lld\n",ans);
    return ;
}

于是我们仅用这么点简洁的代码就A了一道黑题！这道题告诉我：拿到题先分析题目的特性，不要一来就按照传统方式存图，找环，dfs树形DP......

2019-06-26