Java数据结构之算法时间度

1.度量一个程序（算法）执行时间的两种方法

1）事后统计的方法

这种方法可行, 但是有两个问题：一是要想对设计的算法的运行性能进行评测，需要实际运行该程序；二是所得时间的统计量依赖于计算机的硬件、软件等环境因素, 这种方式，要在同一台计算机的相同状态下运行，才能比较那个算法速度更快。

2）事前估算的方法

通过分析某个算法的时间复杂度来判断哪个算法更优。

2.时间频度

基本介绍：一个算法花费的时间与算法中语句的执行次数成正比例，哪个算法中语句执行次数多，它花费时间就多。一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)。

举例说明：比如计算1-100所有数字之和，我们设计两种算法：

T(n) = n + 1 (加1是因为最后要多做一次i <= end判断)

T(n) = 1

3.时间频度举例说明

1）忽略常数项

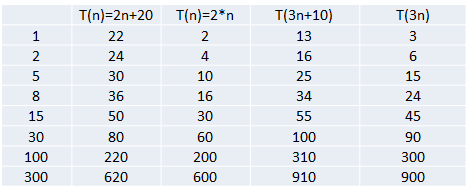
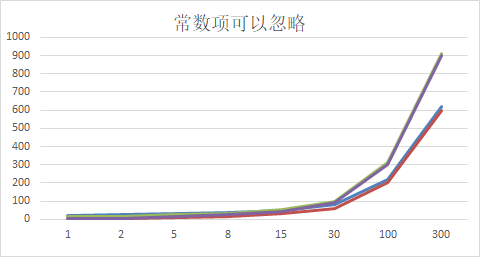
结论：

2n+20 和 2n 随着n 变大，执行曲线无限接近, 20可以忽略

3n+10 和 3n 随着n 变大，执行曲线无限接近, 10可以忽略

2）忽略低次项

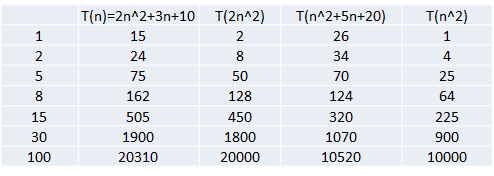
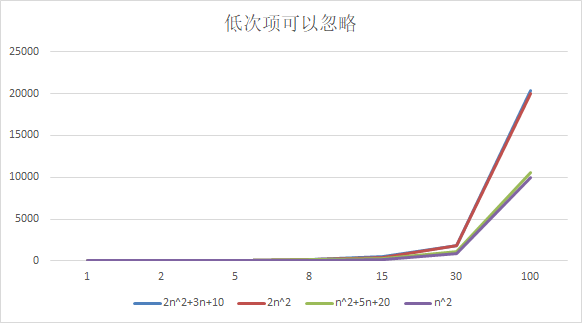
结论：

2n^2+3n+10 和 2n^2 随着n 变大, 执行曲线无限接近, 可以忽略 3n+10

n^2+5n+20 和 n^2 随着n 变大,执行曲线无限接近, 可以忽略 5n+20

3）忽略系数（2次方可忽略，3次方不可以）

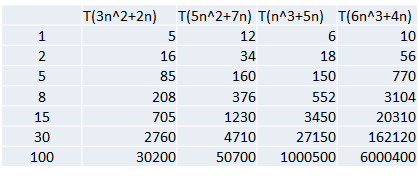
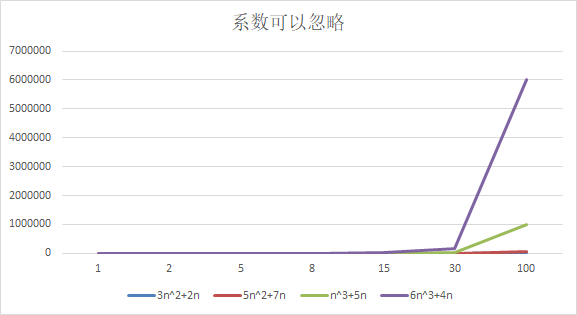
结论：

随着n值变大，5n^2+7n 和 3n^2 + 2n ，执行曲线重合, 说明 这种情况下, 5和3可以忽略。

而n^3+5n 和 6n^3+4n ，执行曲线分离，说明多少次方是关键

4. 时间复杂度

1）一般情况下，算法中的基本操作语句的重复执行次数是问题规模n的某个函数，用T(n)表示，若有某个辅助函数f(n)，使得当n趋近于无穷大时，T(n) / f(n) 的极限值为不等于零的常数，则称f(n)是T(n)的同数量级函数。记作 T(n)=Ｏ( f(n) )，称Ｏ( f(n) )  为算法的渐进时间复杂度，简称时间复杂度。

2）T(n) 不同，但时间复杂度可能相同。 如：T(n)=n²+7n+6 与 T(n)=3n²+2n+2 它们的T(n) 不同，但时间复杂度相同，都为O(n²)。（常数项、低次项、平方系数可忽略）

3）计算时间复杂度的方法：

用常数1代替运行时间中的所有加法常数  T(n)=n²+7n+6 => T(n)=n²+7n+1

修改后的运行次数函数中，只保留最高阶项  T(n)=n²+7n+1 => T(n) = n²

去除最高阶项的系数 T(n) = n² => T(n) = n² => O(n²)

5. 常见的时间复杂度

• 常数阶O(1)：只要是没有循环等，无论代码执行了多少行
• 对数阶O(log₂n)：求2的多少次方为n执行的次数（n个数二分查找log₂n次）默认情况下logN都是以2为底
• 线性阶O(n)：循环里面的代码会执行n遍
• 线性对数阶O(nlog₂n)：将对数阶复杂度的代码循环n遍
• 平方阶O(n²)：把 O(n) 的代码再嵌套循环一遍
• 立方阶O(n³)：相当于三层n循环
• k次方阶O(n^k)：相当于k层n循环
• 指数阶O(2ⁿ)

6. 最优解：先保证时间复杂度最优，再保证空间复杂度最优

说明：

常见的算法时间复杂度由小到大依次为：Ο(1)＜Ο(log₂n)＜Ο(n)＜Ο(nlog₂n)＜Ο(n²)＜Ο(n³)＜ Ο(n^k) ＜Ο(2ⁿ) < O(n!)，随着问题规模n的不断增大，上述时间复杂度不断增大，算法的执行效率越低

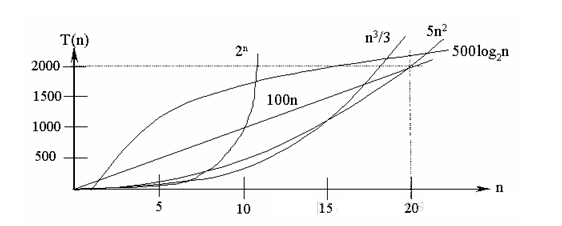
从图中可见，我们应该尽可能避免使用指数阶的算法

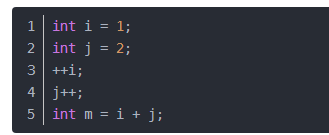
1）常数阶O(1)：

无论代码执行了多少行，只要是没有循环等复杂结构，那这个代码的时间复杂度就都是O(1)

2）对数阶O(log₂n)

说明：在while循环里面，每次都将 i 乘以 2，乘完之后，i 距离 n 就越来越近了。假设循环x次之后，i 就大于 2 了，此时这个循环就退出了，也就是说 2 的 x 次方等于 n，那么 x = log₂n也就是说当循环 log₂n 次以后，这个代码就结束了。因此这个代码的时间复杂度为：O(log₂n) 。 O(log₂n) 的这个2 时间上是根据代码变化的，i = i * 3 ，则是 O(log3n) .

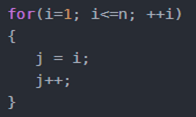
3）线性阶O(n)

说明：for循环里面的代码会执行n遍，因此它消耗的时间是随着n的变化而变化的，因此这类代码都可以用O(n)来表示它的时间复杂度

4）线性对数阶O(nlog₂n)：将对数阶复杂度的代码循环n遍

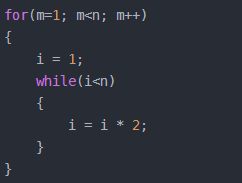
说明：线性对数阶O(nlogN) 其实非常容易理解，将时间复杂度为O(logn)的代码循环N遍的话，那么它的时间复杂度就是 n * O(logN)，也就是了O(nlogN)

5）平方阶O(n²)：把 O(n) 的代码再嵌套循环一遍

说明：这段代码其实就是嵌套了2层n循环，它的时间复杂度就是 O(n*n)，即  O(n²) 如果将其中一层循环的n改成m，那它的时间复杂度就变成了 O(m*n)

6. 平均时间复杂度和最坏时间复杂度

平均时间复杂度：所有可能的输入实例均以等概率出现的情况下，该算法的运行时间。

最坏时间复杂度：最坏情况下的时间复杂度。一般讨论的时间复杂度均是最坏情况下的时间复杂度。

（这样做的原因是：最坏情况下的时间复杂度是算法在任何输入实例上运行时间的界限，这就保证了算法的运行时间不会比最坏情况更长。）

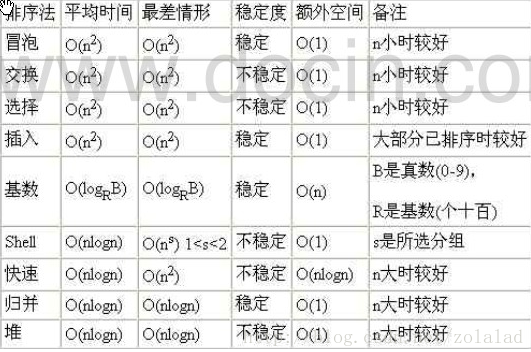
平均时间复杂度和最坏时间复杂度是否一致，和算法有关(如图:)。

各排序算法的时间复杂度对比：

7.空间复杂度

类似于时间复杂度的讨论，一个算法的空间复杂度(Space Complexity)定义为该算法所耗费的存储空间，它也是问题规模n的函数。

空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度。有的算法需要占用的临时工作单元数与解决问题的规模n有关，它随着n的增大而增大，当n较大时，将占用较多的存储单元，例如快速排序和归并排序算法就属于这种情况。

在做算法分析时，主要讨论的是时间复杂度。从用户使用体验上看，更看重的程序执行的速度。一些缓存产品（redis, memcache）和算法（基数排序）本质就是用空间换时间。