浅谈Manacher算法

Manacher

manacher是一种\(O(n)\)求最长回文子串的算法，俗称马拉车（滑稽）

直接步入正题

首先可以知道的是：每一个回文串都有自己的对称中心，相应的也有自己的最大延伸长度（可以称之为“半径”）

我们设\(rad[i]\)表示以\(i\)为中心的回文子串的半径，那么只需要知道所有的\(rad[i]\)就可以求出最长回文子串了

从\(1\)到\(n\)枚举\(i\)，求解\(rad[i]\)

设当前已经求到了\(rad[k]\)，设前\(k-1\)个数中\(rad[i]+i\)（即右端点）最大的数为\(mid\)，令\(r=mid+rad[mid]\)

那么可以证明一个点\(i\)关于\(mid\)的对称点是\(2\times mid-i\)（两点距离公式）

opt1：如果\(k\leq r\)

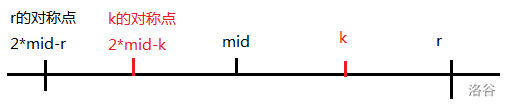
方便起见，令\(j=2\times mid-k\)

1.若\(j-rad[j]>mid-rad[mid]\)，即以\(j\)点为中心的最长回文子串的左端点在以\(mid\)为中心的最长回文子串的左端点右边，则\(rad[i]\)可以直接由\(rad[j]\)转移过来（因为\(2\times mid-r\)_{$mid$和$mid$}\(r\)是对称的，所以\(k\)的半径和\(j\)的半径是一样的），即\(rad[i]=rad[j]\)

2.若\(j-rad[j]\leq mid-rad[mid]\)，则\(rad[k]\)至少是\(r-k\)。接下来再暴力延伸，顺便更新\(mid\)和\(r\)

opt2：如果\(k>r\)

直接暴力延伸，顺便更新\(mid\)和\(r\)

可以发现每次暴力延伸的时候，暴力延伸多少，\(r\)也会变化多少，且\(r\)是递增的且不超过\(n\)的数

关于复杂度：

由于每一个字符最多只会被遍历一次，所以复杂度是\(O(n)\)的

实现细节：

1.由于长度为偶数的回文串对称中心并不能实际找到，所以在两个字符之间插入#。这样不会影响答案，并且可以解决这个问题

2.对于不同情况的相似之处可以合并到一起来降低码量，如op1.1的直接转移和opt1.2的转移等

3.不要忘了更新\(mid\)和\(r\)

4.注意下标

代码：

#include<bits/stdc++.h>
using namespace std;
char cString[22000005];
int iRad[22000005];
int iLen,iAns;

void read()
{
	char c = getchar();
	cString[0] = '|', cString[++iLen] = '#';
	while(c < 'a' || c > 'z') c = getchar();
	while(c >= 'a'&& c <= 'z') cString[++iLen] = c, cString[++iLen] = '#', c = getchar();
}

int main()
{
	read();//读入
	for(int i = 1, mid = 0, r = 0; i <= iLen; i++)
	{
		if(i <= r) iRad[i] = min(iRad[mid * 2 - i], r - i + 1);//opt1
		while(cString[i - iRad[i]] == cString[i + iRad[i]]) ++iRad[i];//opt1.2,opt2 尝试暴力延伸
		if(i + iRad[i] > r) r = i + iRad[i] - 1, mid = i;//更新mid和r
		if(iRad[i] > iAns) iAns = iRad[i];//更新答案
	}
	printf("%d", iAns-1);
}