[洛谷P1514] NOIP2010 引水入城

问题描述

在一个遥远的国度，一侧是风景秀美的湖泊，另一侧则是漫无边际的沙漠。该国的行政区划十分特殊，刚好构成一个N 行×M 列的矩形，如上图所示，其中每个格子都代表一座城市，每座城市都有一个海拔高度。

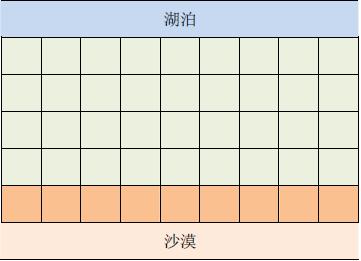
为了使居民们都尽可能饮用到清澈的湖水，现在要在某些城市建造水利设施。水利设施有两种，分别为蓄水厂和输水站。蓄水厂的功能是利用水泵将湖泊中的水抽取到所在城市的蓄水池中。

因此，只有与湖泊毗邻的第1行的城市可以建造蓄水厂。而输水站的功能则是通过输水管线利用高度落差，将湖水从高处向低处输送。故一座城市能建造输水站的前提，是存在比它海拔更高且拥有公共边的相邻城市，已经建有水利设施。由于第N行的城市靠近沙漠，是该国的干旱区，所以要求其中的每座城市都建有水利设施。那么，这个要求能否满足呢？如果能，请计算最少建造几个蓄水厂；如果不能，求干旱区中不可能建有水利设施的城市数目。

输入格式

每行两个数，之间用一个空格隔开。输入的第一行是两个正整数N,M，表示矩形的规模。接下来N行，每行M个正整数，依次代表每座城市的海拔高度。

输出格式

两行。如果能满足要求，输出的第一行是整数11，第二行是一个整数，代表最少建造几个蓄水厂；如果不能满足要求，输出的第一行是整数00，第二行是一个整数，代表有几座干旱区中的城市不可能建有水利设施。

样例输入输出

样例输入1

2 5

9 1 5 4 3

8 7 6 1 2

样例输出1

1

1

样例输入2

3 6

8 4 5 6 4 4

7 3 4 3 3 3

3 2 2 1 1 2

样例输出2

1

3

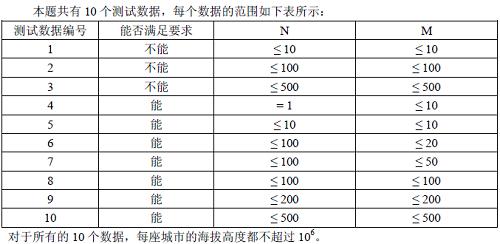
数据范围

解析

首先，我们需要发现题目的一个性质：在满足要求的情况下，一个水利设施能够覆盖到的最后一排的城市一定是连续的一段。否则中间无法被覆盖的地方也同样不能被其他水利设施覆盖。那么，我们可以用记忆化搜索的形式得到每个格子能够覆盖的区间。验证可行性时只用判断最后一行是否都访问到了即可。

然后，对于每一个第一行的格子，都有一个区间的范围。问题转化为了用最少的线段覆盖整个最后一行。将每个线段按左端点排序，每次取左端点在当前覆盖的区间中的右端点最远的线段，直到完全覆盖。

代码

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#define N 502
using namespace std;
struct node{
    int l,r;
}a[N];
int dx[4]={1,-1,0,0},dy[4]={0,0,1,-1};
int n,m,i,j,h[N][N],l[N][N],r[N][N];
bool vis[N][N];
int read()
{
    char c=getchar();
    int w=0;
    while(c<'0'||c>'9') c=getchar();
    while(c<='9'&&c>='0'){
        w=w*10+c-'0';
        c=getchar();
    }
    return w;
}
bool in(int x,int y)
{
    return x>=1&&x<=n&&y>=1&&y<=m;
}
void dfs(int x,int y)
{
    if(vis[x][y]) return;
    if(x==n) l[x][y]=r[x][y]=y;
    vis[x][y]=1;
    for(int i=0;i<4;i++){
        int tx=x+dx[i],ty=y+dy[i];
        if(in(tx,ty)&&h[tx][ty]<h[x][y]){
            dfs(tx,ty);
            l[x][y]=min(l[x][y],l[tx][ty]);
            r[x][y]=max(r[x][y],r[tx][ty]);
        }
    }
}
int my_comp(const node &x,const node &y)
{
    return x.l<y.l;
}
int main()
{
    memset(l,0x3f,sizeof(l));
    n=read();m=read();
    for(i=1;i<=n;i++){
        for(j=1;j<=m;j++) h[i][j]=read();
    }
    for(i=1;i<=m;i++) dfs(1,i);
    int cnt=0,ans=0,maxr=1,minl=0;
    for(i=1;i<=m;i++){
        if(!vis[n][i]) cnt++;
    }
    if(cnt){
        cout<<"0"<<endl<<cnt<<endl;
        return 0;
    }
    for(i=1;i<=m;i++) a[i].l=l[1][i],a[i].r=r[1][i];
    sort(a+1,a+m+1,my_comp);
    int lx=1;
    while(lx<=m){
        int rx=0;
        for(i=1;i<=m;i++){
            if(l[1][i]<=lx) rx=max(rx,r[1][i]);
        }
        ans++;
        lx=rx+1;
    }
    cout<<"1"<<endl<<ans<<endl;
    return 0;
}