dp或dfs(01背包问题)

链接：https://ac.nowcoder.com/acm/contest/993/C
来源：牛客网
题意：n头牛，给出它们的H高度，问这些牛的高度叠加起来大于等于书架高度，问叠加后的高度与书架的差值最小为多少？

1解法：01背包容量枚举从书架高度到所有牛高度总和的高度，遍历从书架高度容量开始，取可满足容量的最小值。

dp【j】表示背包容量为j时，所能装下的最大物品重量。

//#include <bits/stdc++.h>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <iostream>
#include <algorithm>
#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <stdio.h>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <string.h>
#include <vector>
#define ME(x , y) memset(x , y , sizeof(x))
#define SF(n) scanf("%d" , &n)
#define rep(i , n) for(int i = 0 ; i < n ; i ++)
#define INF  0x3f3f3f3f
#define mod 1000000007
#define PI acos(-1)
using namespace std;
typedef long long ll ;
int w[20] , dp[1000009];

int main()
{
    int n , h ;
    scanf("%d%d" , &n , &h);
    int sum = 0 ;
    for(int i = 1 ; i <= n ; i++)
    {
        scanf("%d" , &w[i]);
        sum += w[i];
    }
    memset(dp,  0 , sizeof(dp));
    for(int i = 1 ; i <= n ; i++)
    {
        for(int j = sum ; j >= w[i] ; j--)
        {
            dp[j] = max(dp[j] , dp[j-w[i]]+w[i]);
        }
    }
    int ans = INF ;
    for(int i = h ; i <= sum ; i++)
    {
        if(dp[i] >= h)
        ans = min(ans , abs(dp[i] - h));
    }
    cout << ans << endl ;

    return 0;
}

2解法：因为牛数量较少，可以dfs搜索所有可能的牛叠加的高度情况

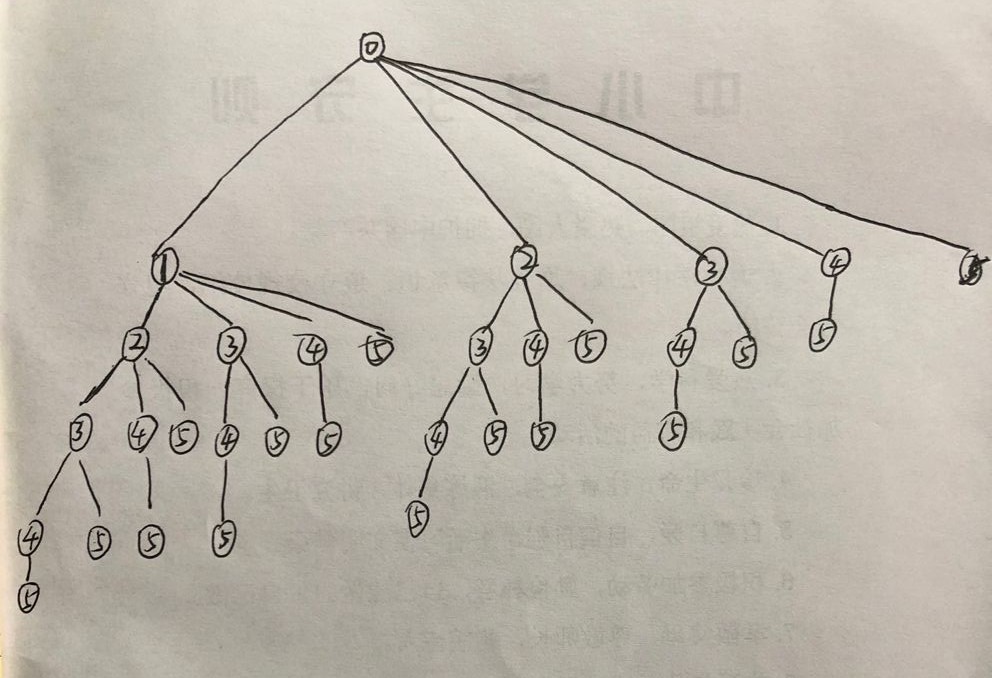
//#include <bits/stdc++.h>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <iostream>
#include <algorithm>
#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <stdio.h>
#include <queue>
#include <stack>;
#include <map>
#include <set>
#include <ctype.h>
#include <string.h>
#include <vector>
#define ME(x , y) memset(x , y , sizeof(x))
#define SF(n) scanf("%d" , &n)
#define rep(i , n) for(int i = 0 ; i < n ; i ++)
#define INF  0x3f3f3f3f
#define mod 10
#define PI acos(-1)
using namespace std;
typedef long long ll ;
int n , m , ans ;
int a[];
void dfs(int s , int l)
{
    if(s >= m)
    {
        ans = min(ans , s - m);
        return ;
    }
    for(int i = l ; i < n ; i++)
    {
        dfs(s+a[i] , i+);
    }
}

int main()
{

    scanf("%d%d" , &n , &m);
    for(int i =  ; i < n ; i++)
    {
        scanf("%d" , &a[i]);
    }
    ans = INF ;
    dfs( , );
    cout << ans << endl ;

    return ;
}