HDU 2065 “红色病毒”问题 --指数型母函数

这种有限制的类棋盘着色问题一般可以用指数型母函数来解决，设Hn表示这样的着色数，首先H0=1,则Hn等于四个字母的（A,B,C,D）的多重集合的n排列数，其中每个字母的重数是无穷，且要求A,C出现的次数是偶数，因此，H0,H1,...Hn,...的指数生成函数是A,B,C,D因子的乘积：

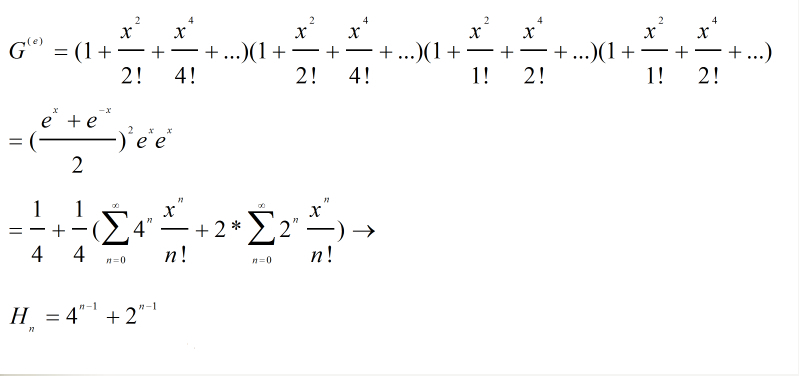
用快速幂解决，只不过在HDU不能用long long解决，要用__int64.

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#define lll __int64
#define ll long long
using namespace std;
#define N 250007

int fastm(int a,ll b,int m)
{
    int t=;
    while(b)
    {
        if(b&1LL)
            t=(t*a)%m;
        b >>= ;
        a=(a*a)%m;
    }
    return t;
}

int main()
{
    int t,i;
    ll n;
    int cs;
    while(scanf("%d",&t)!=EOF && t)
    {
        cs = ;
        while(t--)
        {
            scanf("%I64d",&n);
            int res = fastm(,n-1LL,) + fastm(,n-1LL,);
            res %= ;
            printf("Case %d: %d\n",cs++,res);
        }
        puts("");
    }
    return ;
}