[LeetCode] next_permutation

概念

全排列的生成算法有很多种，有递归遍例，也有循环移位法等等。C++/STL中定义的next_permutation和prev_permutation函数则是非常灵活且高效的一种方法，它被广泛的应用于为指定序列生成不同的排列。本文将详细的介绍prev_permutation函数的内部算法。

按照STL文档的描述，next_permutation函数将按字母表顺序生成给定序列的下一个较大的序列，直到整个序列为减序为止。prev_permutation函数与之相反，是生成给定序列的上一个较小的序列。二者原理相同，仅遍例顺序相反，这里仅以next_permutation为例介绍算法。

下文内容都基于一个假设，即序列中不存在相同元素。对序列大小的比较做出定义：两个长度相同的序列，从两者的第一个元素开始向后比较，直到出现一个不同元素（也可能就是第它们的第一个元素），该元素较大的序列为大，反之序列为小；若一直到最后一个元素都相同，那么两个序列相等。

设当前序列为p_n，下一个较大的序列为p_n+1，那么不存在p_m，使得p_n < p_m < p_n+1。

问题

给定任意非空序列，生成下一个较大或较小的序列。

数学推导

根据上述概念易知，对于一个任意序列，最小的序列是增序，最大的序列为减序。那么给定一个p_n要如何才能生成p_n+1呢？先来看下面的例子：

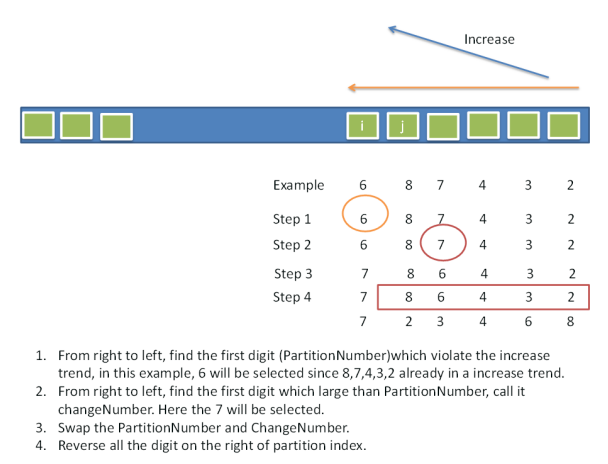
我们用<a₁ a₂ ... a_m>来表示m个数的一种序列。设序列p_n=<3 6 4 2>，根据定义可算得下一个序列p_n+1=<4 2 3 6>。观察p_n可以发现，其子序列<6 4 2>已经为减序，那么这个子序列不可能通过交换元素位置得出更大的序列了，因此必须移动最高位3（即a₁）的位置，且要在子序列<6 4 2>中找一个数来取代3的位置。子序列<6 4 2>中6和4都比3大，但6大于4。如果用6去替换3得到的序列一定会大于4替换3得到的序列，因此只能选4。将4和3的位置对调后形成排列<4 6 3 2>。对调后得到的子序列<6 3 2>仍保持减序，即这3个数能够生成的最大的一种序列。而4是第1次作为首位的，需要右边的子序列最小，因此4右边的子序列应为<2 3 6>，这样就得到了正确的一个序列p_n+1=<4 2 3 6>。

下面归纳分析该过程。假设一个有m个元素的序列p_n，其下一个较大序列为p_n+1。

1) 若p_n最右端的2个元素构成一个增序子序列，那么直接反转这2个元素使该子序列成为减序，即可得到p_n+1。

2) 若p_n最右端一共有连续的s个元素构成一个减序子序列，令i = m - s，则有p_n(i) < p_n(i+1)，其中p_n(i)表示排列p_n的第i个元素。例如p_n=<1 2 5 4 3>，那么p_n的右端最多有3个元素构成一个减序子集<5 4 3>，i=5-3=2，则有p_n(i)=2 < 5=p_n(i+1)。因此若将p_n(i)和其右边的子集s {p_n(i+1), p_n(i+2), ..., p_n(m)}中任意一个元素调换必能得到一个较大的序列（不一定是下一个）。要保证是下一个较大的序列，必须保持p_n(i)左边的元素不动，并在子集s {p_n(i+1), p_n(i+2), ..., p_n(m)}中找出所有比p_n(i)大的元素中最小的一个p_n(j)，即不存在p_n(k) ∈ s且p_n(i) < p_n(k) < p_n(j)，然后将二者调换位置。现在只要使新子集{p_n(i+1), p_n(i+2), ..., p_n(i), ...,p_n(m)}成为最小序列即得到p_n+1。注意到新子集仍保持减序，那么此时直接将其反转即可得到p_n+1 {p_n(1), p_n(2), ..., p_n(j), p_n(m), p_n(m-1), ..., p_n(i), ..., p_n(i+2), p_n(i+1)}。

复杂度

最好的情况为p_n的最右边的2个元素构成一个最小的增序子集，交换次数为1，复杂度为O(1)，最差的情况为1个元素最小，而右面的所有元素构成减序子集，这样需要先将第1个元素换到最右，然后反转右面的所有元素。交换次数为1+(n-1)/2，复杂度为O(n)。因为各种排列等可能出现，所以平均复杂度即为O(n)。

扩展

1. 能否直接算出集合{1, 2, ..., m}的第n个排列？

设某个集合{a₁, a₂, ..., a_m}（a₁<a₂<...<a_m）构成的某种序列p_n，基于以上分析易证得：若a_s<a_t，那么将a_s作为第1个元素的所有序列一定都小于a_t作为第1个元素的任意序列。同理可证得：第1个元素确定后，剩下的元素中若a_s'<a_t'，那么将a_s'作为第2个元素的所有序列一定都小于作为第2个元素的任意序列。例如4个数的集合{2, 3, 4, 6}构成的序列中，以3作为第1个元素的序列一定小于以4或6作为第1个元素的序列；3作为第1个元素的前题下，2作为第2个元素的序列一定小于以4或6作为第2个元素的序列。

推广可知，在确定前i（i<n）个元素后，在剩下的m-i=s个元素的集合{a_q1, a_q2, ..., a_q3}（a_q1<a_q2<...<a_qm）中，以a_qj作为第i+1个元素的序列一定小于以a_qj+1作为第i+1个元素的序列。由此可知：在确定前i个元素后，一共可生成s!种连续大小的序列。

根据以上分析，对于给定的n（必有n<=m!）可以从第1位开始向右逐位地确定每一位元素。在第1位不变的前题下，后面m-1位一共可以生成(m-1)!中连续大小的序列。若n>(m-1)!，则第1位不会是a₁，n中可以容纳x个(m-1)!即代表第1位是a_x。在确定第1位后，将第1位从原集合中删除，得到新的集合{a_q1, a_q2, ..., a_q3}（a_q1<a_q2<...<a_qm），然后令n₁=n-x(m-1)!，求这m-1个数中生成的第n₁个序列的第1位。

举例说明：如7个数的集合为{1, 2, 3, 4, 5, 6, 7}，要求出第n=1654个排列。

(1654 / 6!)取整得2，确定第1位为3，剩下的6个数{1, 2, 4, 5, 6, 7}，求第1654 % 6!=214个序列；

(214 / 5!)取整得1，确定第2位为2，剩下5个数{1, 4, 5, 6, 7}，求第214 % 5!=94个序列；

(94 / 4!)取整得3，确定第3位为6，剩下4个数{1, 4, 5, 7}，求第94 % 4!=22个序列；

(22 / 3!)取整得3，确定第4位为7，剩下3个数{1, 4, 5}，求第22 % 3!=4个序列；

(4 / 2!)得2，确定第5为5，剩下2个数{1, 4}；由于4 % 2!=0，故第6位和第7位为增序<1 4>；

因此所有排列为：3267514。

2. 给定一种排列，如何算出这是第几个排列呢？

和前一个问题的推导过程相反。例如3267514：

后6位的全排列为6!，3为{1, 2, 3 ,4 , 5, 6, 7}中第2个元素（从0开始计数），故2*720=1440；

后5位的全排列为5!，2为{1, 2, 4, 5, 6, 7}中第1个元素，故1*5!=120；

后4位的全排列为4!，6为{1, 4, 5, 6, 7}中第3个元素，故3*4!=72；

后3位的全排列为3!，7为{1, 4, 5, 7}中第3个元素，故3*3!=18；

后2位的全排列为2!，5为{1, 4, 5}中第2个元素，故2*2!=4；

最后2位为增序，因此计数0，求和得：1440+120+72+18+4=1654

next_Permutation Code 如下

 class Solution {
     public:
         void nextPermutation(vector<int> &num) {
             // Start typing your C/C++ solution below
             // DO NOT write int main() function
             int i;
             vector<int>::iterator iter = num.end();
             int maxNum = INT_MIN;

             //step 1, find the first number which violate the increase form right to left, we call it AAA
             // take 5 6 7 8 4 3 2 1 for a example, find AAA = 7;
             for(i = num.size() - ; i >= ; i--)
             {
                 if (num[i] < num[i+])
                     break;
             }   

             if (i >= ) //i found
             {
                 int j;
                 int minNum = INT_MAX;
                 //step 2, find the first number which is large than AAA form right to left, we call it BBB
                 // take 5 6 7 8 4 3 2 1 for a example, find BBB = 8;
                 for(j = num.size() - ; j >= ; j--)
                 {
                     if (num[j] > num[i])
                         break;
                 }

                 //step 3, swap AAA and BBB
                 // take 5 6 7 8 4 3 2 1 for a example, exchanged array is 5 6 8 7 4 3 2 1
                 int t = num[i];
                 num[i] = num[j];
                 num[j] = t;

                 //step 4, reverse all digit after AAA's position
                 // take 5 6 7 8 4 3 2 1 for a example, exchanged array is 5 6 8 7 4 3 2 1, then reverse 7 4 3 2 1
                 // the output array is 5 6 8 1 2 3 4 7
                 int k = i + ;
                 j =  num.size() - ;
                 while(k < j)
                 {
                     t = num[k];
                     num[k] = num[j];
                     num[j] = t;

                     k++;
                     j--;
                 }
             }
             else
                 //sort(num.begin(), num.end());
             {
                 int k = ;
                 int j =  num.size() - ;
                 while(k < j)
                 {
                     int t = num[k];
                     num[k] = num[j];
                     num[j] = t;

                     k++;
                     j--;
                 }
             }
         }
 };

总结：

next_permutation的实现过程如下：

首先，从最尾端开始往前寻找两个相邻的元素，令第一个元素是i, 第二个元素是ii,且满足i<ii； （找破坏了递增的那个元素AAA，位置m）

然后，再从最尾端开始往前搜索，找出第一个大于i的元素，设其为j；（找比AAA大的元素BBB）

然后，将i和j对调，再将ii及其后面的所有元素反转。（交换AAA 和BBB，然后reverse m右边的元素）

这样得到的新序列就是“下一个排列”。

　　prev_permutation的实现过程如下：

首先，从最尾端开始向前寻找两个相邻的元素，令第一个元素为i,第二个元素为ii,且满足i>ii（找破坏了递减的那个元素AAA，位置m）

然后，从最尾端开始往前寻找第一个小于i的元素，令它为j（找比AAA小的元素BBB）

然后，将i和j对调，再将ii及其之后的所有元素反转。（交换AAA 和BBB，然后reverse m右边的元素）

　　　　这样得到的序列就是该排列的上一个排列。