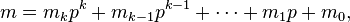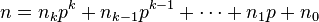lucas定理,组合数学问题
对于C(n, m) mod p。这里的n,m,p(p为素数)都很大的情况。就不能再用C(n, m) = C(n - 1,m) + C(n - 1, m - 1)的公式递推了。
这里用到Lusac定理
For non-negative integers m and n and a prime p, the following congruence relation holds:
where
and
are the base p expansions of m and n respectively.
对于单独的C(ni, mi) mod p,已知C(n, m) mod p = n!/(m!(n - m)!) mod p。显然除法取模,这里要用到m!(n-m)!的逆元。
根据费马小定理:
已知(a, p) = 1,则 ap-1 ≡ 1 (mod p), 所以 a*ap-2 ≡ 1 (mod p)。
也就是 (m!(n-m)!)的逆元为 (m!(n-m)!)p-2 ;
代码:

typedef long long LL;
using namespace std; LL exp_mod(LL a, LL b, LL p) {
LL res = 1;
while(b != 0) {
if(b&1) res = (res * a) % p;
a = (a*a) % p;
b >>= 1;
}
return res;
} LL Comb(LL a, LL b, LL p) {
if(a < b) return 0;
if(a == b) return 1;
if(b > a - b) b = a - b; LL ans = 1, ca = 1, cb = 1;
for(LL i = 0; i < b; ++i) {
ca = (ca * (a - i))%p;
cb = (cb * (b - i))%p;
}
ans = (ca*exp_mod(cb, p - 2, p)) % p;
return ans;
} LL Lucas(int n, int m, int p) {
LL ans = 1; while(n&&m&&ans) {
ans = (ans*Comb(n%p, m%p, p)) % p;
n /= p;
m /= p;
}
return ans;
} int main() {
Read();
int n, m, p;
while(~scanf("%d%d%d", &n, &m, &p)) {
printf("%lld\n", Lucas(n, m, p));
}
return 0;
}

lucas定理,组合数学问题的更多相关文章
- Bzoj 4403: 序列统计 Lucas定理,组合数学,数论
4403: 序列统计 Time Limit: 3 Sec Memory Limit: 128 MBSubmit: 328 Solved: 162[Submit][Status][Discuss] ...
- BZOJ4403: 序列统计【lucas定理+组合数学】
Description 给定三个正整数N.L和R,统计长度在1到N之间,元素大小都在L到R之间的单调不降序列的数量.输出答案对10^6+3取模的结果. Input 输入第一行包含一个整数T,表示数据组 ...
- HDU 5226 Tom and matrix(组合数学+Lucas定理)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=5226 题意:给一个矩阵a,a[i][j] = C(i,j)(i>=j) or 0(i < ...
- lucas定理和组合数学
自湖南长沙培训以来的坑...一直未填,今天把这个问题解决掉. 参考: 1.http://www.cnblogs.com/Var123/p/5523068.html 2.http://blog.csdn ...
- Lucas定理及应用
额,前两天刚讲了数据结构,今天我来讲讲组合数学中的一种奇妙优化——Lucas 先看这样一个东西 没学过lucas的肯定会说:还不简单?处理逆元,边乘边膜呗 是,可以,但注意一下数据范围 你算这一次,你 ...
- [学习笔记]扩展LUCAS定理
可以先做这个题[SDOI2010]古代猪文 此算法和LUCAS定理没有半毛钱关系. [模板]扩展卢卡斯 不保证P是质数. $C_n^m=\frac{n!}{m!(n-m)!}$ 麻烦的是分母. 如果互 ...
- hdu 3037 费马小定理+逆元除法取模+Lucas定理
组合数学推推推最后,推得要求C(n+m,m)%p 其中n,m小于10^9,p小于1^5 用Lucas定理求(Lucas定理求nm较大时的组合数) 因为p数据较小可以直接阶乘打表求逆元 求逆元时,由费马 ...
- Lucas定理初探
1.1 问题引入 已知\(p\)是一质数,求\(\dbinom{n}{m}\pmod{p}\). 关于组合数,它和排列数都是组合数学中的重要概念.这里会张贴有关这两个数的部分内容. 由于Lucas定理 ...
- 【HDU 3037】Saving Beans Lucas定理模板
http://acm.hdu.edu.cn/showproblem.php?pid=3037 Lucas定理模板. 现在才写,noip滚粗前兆QAQ #include<cstdio> #i ...
- CF451E Devu and Flowers (隔板法 容斥原理 Lucas定理 求逆元)
Codeforces Round #258 (Div. 2) Devu and Flowers E. Devu and Flowers time limit per test 4 seconds me ...
随机推荐
- 练习一_使用Git进行代码管理的心得
2015年9月19日,第一次软工实践课.助教给我们介绍了git,GitHub.显而易见,我并没有听懂.所以整个上午都在找教程,一个字一个字对着敲,然后敲着敲着就出错,回宿舍,继续敲,也是一样的... ...
- struts1日期转换处理
问题场景 最近在维护公司旧的系统(用的struts1框架)的时候,在日期处理的时候,我将日期设定为Date类型,结果报以下错误: javax.servlet.ServletException: Bea ...
- Spring-事物的隔离级别
Spring中定义了5中不同的事务隔离级别: 1. ISOLATION_DEFAULT(一般情况下使用这种配置既可) ; 这是一个PlatfromTransactionManager默认的隔离级别,使 ...
- 【蒟蒻の进阶PLAN】 置顶+持续连载
看到周围神犇们纷纷列计划,本蒟蒻也决定跟随他们的步伐,计划大约是周计划吧,具体怎么安排我也不确定.. 2015.12.30 刚刚学习完最基础的网络流,需要进行这方面的练习,从简到难,有空余的话尝试学习 ...
- 直接运行可执行文件linux终端一闪而过
运行elasticsearch的时候进入bin目录,ela 然后tab提示的内容中没有e..s..,很奇怪,然后我直接双击运行es,终端一闪而过,我就手动打开终端, ./elasticsearch 这 ...
- 【bzoj1211】 HNOI2004—树的计数
http://www.lydsy.com/JudgeOnline/problem.php?id=1211 (题目链接) 题意 一个有n个结点的树,设它的结点分别为v1, v2, …, vn,已知第i个 ...
- 【bzoj2823】 AHOI2012—信号塔
http://www.lydsy.com/JudgeOnline/problem.php?id=2823 (题目链接) 题意 求最小圆覆盖 Solution 关于最小圆覆盖的做法,论文里面都有.其实真 ...
- Erlang之父的学习历史及学习建议
当我开始学习编程的时候(1967年),我可以在 FORTRAN 和(传说中的)Algol 之间选择,不过没有任何人了解 Algol,所以我选择了 FORTRAN. 在我最早学习编程的时候,我的编程周期 ...
- C++ 中的名称冲突之 "y1"
已经是第二次遇到这个问题了: #include <bits/stdc++.h> using namespace std; ); ][N][][N]; int x1, x2, y1, y2; ...
- javascript-如何判断一个对象为数组
Q:如何判断一个对象是否为数组? A1:判断对象的constructor是否指向Array, 接着判断对应的特殊属性,如length,splice之类.这个很容易冒充. A2:使用instanceof ...