Douglas Peucker算法的C#实现

一、算法原理

Douglas-Peucker算法

在数字化过程中，需要对曲线进行采样简化，即在曲线上取有限个点，将其变为折线，并且能够在一定程度

上保持原有的形状。

经典的Douglas-Peucker算法描述如下：

（1）在曲线首尾两点A，B之间连接一条直线AB，该直线为曲线的弦；

（2）得到曲线上离该直线段距离最大的点C，计算其与AB的距离D；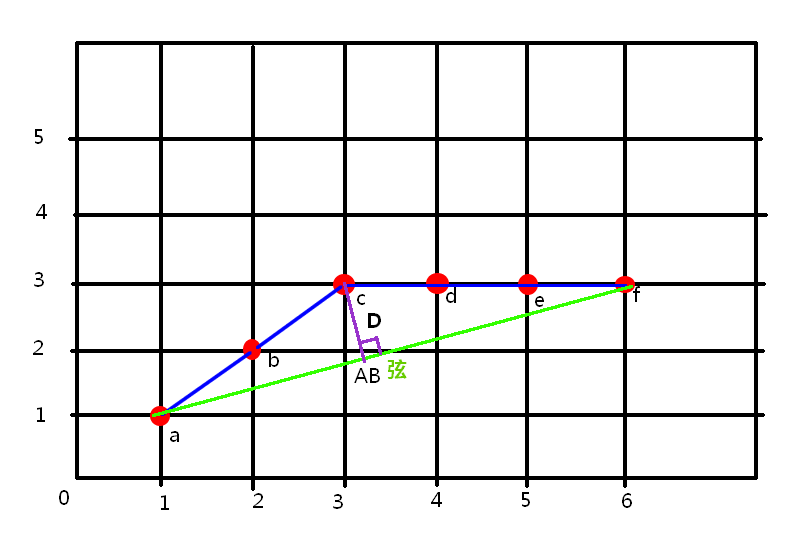

（3）比较该距离与预先给定的阈值threshold的大小，如果小于threshold，则该直线段作为曲线的近似，该段曲线处理完毕。

（4）如果距离大于阈值，则用C将曲线分为两段AC和BC，并分别对两段取信进行1~3的处理。

（5）当所有曲线都处理完毕时，依次连接各个分割点形成的折线，即可以作为曲线的近似。

二、算法C#实现

 using System;
 using System.Collections.Generic;
 using System.Linq;
 using System.Text;

 namespace ConsoleApplication2
 {
     public struct cvPoint
     {
         public int X;
         public int Y;
         public cvPoint(int x, int y)
         {
             X = x;
             Y = y;
         }
     }
     class Program
     {
         static void Main(string[] args)
         {
             var points = new List<cvPoint>();
             points.Add(new cvPoint(, ));
             points.Add(new cvPoint(, ));
             points.Add(new cvPoint(, ));
             points.Add(new cvPoint(, ));
             points.Add(new cvPoint(, ));
             points.Add(new cvPoint(, ));
             points.Add(new cvPoint(, ));
             points.Add(new cvPoint(, ));
             points.Add(new cvPoint(, ));
             points.Add(new cvPoint(, ));
             var epsilon = 0.8d;
             var filteredPoints = new List<cvPoint>();
             DouglasPeucker(points, epsilon, ref filteredPoints);
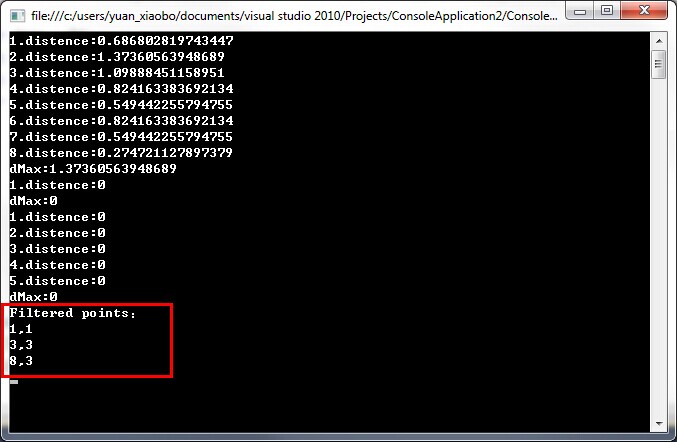
             Console.WriteLine("Filtered points：");
             foreach (var f in filteredPoints)
             {
                 Console.WriteLine(string.Format("{0},{1}", f.X, f.Y));
             }
             Console.ReadKey();
         }
         private static double distanceToSegment(cvPoint p, cvPoint start, cvPoint end)
         {
             var m1 = ((double)(end.Y - start.Y)) / ((double)(end.X - start.X));
             var c1 = start.Y - m1 * start.X;
             var interPointX = 0d;
             var interPointY = 0d;
             if (m1 == )
             {
                 interPointX = p.X;
                 interPointY = c1;

             }
             else
             {
                 var m2 = - / m1;
                 var c2 = p.Y - m2 * p.X;
                 interPointX = (c1 - c2) / (m2 - m1);
                 interPointY = m2 * interPointX + c2;
             }
             return Math.Sqrt(Math.Pow(p.X - interPointX, ) + Math.Pow(p.Y - interPointY, ));
         }

         private static void DouglasPeucker(IList<cvPoint> PointList, double epsilon, ref List<cvPoint> filteredPoints)
         {
             var dmax = 0d;
             int index = ;
             int length = PointList.Count;
             for (int i = ; i < length - ; i++)
             {
                 var d = distanceToSegment(PointList[i], PointList[], PointList[length - ]);
                 Console.WriteLine(string.Format("{0}.distence:{1}", i, d));
                 if (d > dmax)
                 {
                     index = i;
                     dmax = d;
                 }
             }
             Console.WriteLine(string.Format("dMax:{0}", dmax));
             // If max distance is greater than epsilon, recursively simplify
             if (dmax > epsilon)
             {
                 filteredPoints.Add(PointList[]);
                 filteredPoints.Add(PointList[index]);
                 filteredPoints.Add(PointList[length - ]);
                 DouglasPeucker(PointList.Take(index + ).ToList(), epsilon, ref filteredPoints);
                 DouglasPeucker(PointList.Skip(index + ).Take(PointList.Count - index - ).ToList(), epsilon, ref filteredPoints);
             }
         }
     }
 }

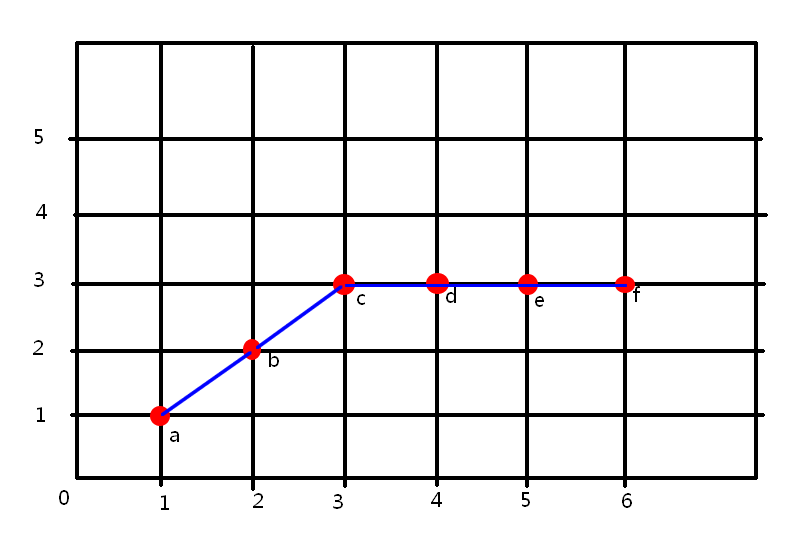
三、算法验证
近似前：

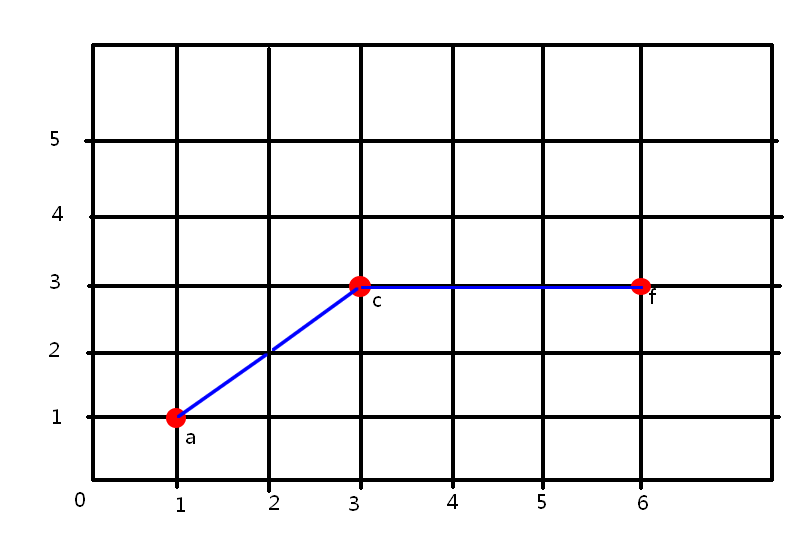
近似后的线段：

本文地址： http://www.cnblogs.com/deepleo/p/Douglas-Peucker.html

参考：http://www.codeproject.com/Articles/18936/A-C-Implementation-of-Douglas-Peucker-Line-Approxi