斯坦福CS229机器学习课程笔记 part2：分类和逻辑回归 Classificatiion and logistic regression

Logistic Regression 逻辑回归

1.模型

逻辑回归解决的是分类问题，并且是二元分类问题(binary classification)，y只有0，1两个取值。对于分类问题使用线性回归不行，因为直线无法将样本正确分类。

1.1 Sigmoid Function

因为 y∈{0,1}，我们也希望 h_θ(x)∈{0,1}。第一种选择是 logistic函数或S型函数(logistic function/sigmoid function)。g(z)值的范围在0-1之间，在z=0时为0.5，z无穷小g(z)趋近0，z无穷大g(z)趋近1。

其公式为：

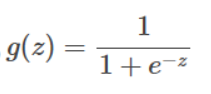
图像为：

同时g(z)的倒数有以下这个特性，即g(z)的倒数刚好等于 g(z)(1-g(z))：

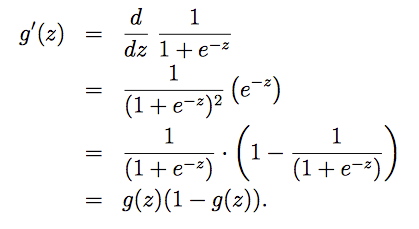
假设 h_θ(x) 的公式为：

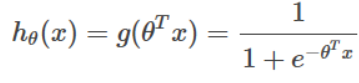
1.2 threshold function

logistic函数是曲线，如果想更加明确地将输出分为0、1两类，就要用到阶梯函数／临界函 (threshold function)。很简单直白的定义：

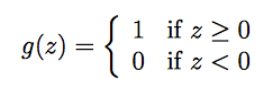
如果使用threshold函数替换logistic函数，则算法称为感知学习算法(Perceptron learning algorithm)。

2.策略

下面根据逻辑回归模型，调整 θ 对其进行拟合。首先进行以下假设：

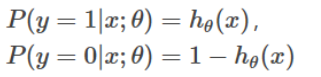
两个式子可以改写成一个式子：

逻辑回归使用的策略是最大化对数似然函数。似然函数 likelihood function 与对数似然函数分别为：

注：似然函数，就是计算整个训练集中每组 x,y 成立的可能性，即将每一组 x⁽ⁱ⁾,y⁽ⁱ⁾ 发生的概率相乘。

求对数是为了计算方便

3.算法

逻辑回归的目的是使可能性最大，即 maximizing 最大化似然函数的值。（线性回归是为了使代价最小，即minimizing代价函数的值，求最低点）

3.1 gradient ascent 梯度上升

先假设只有一个训练样本，对函数 l(θ) 求偏导可得：

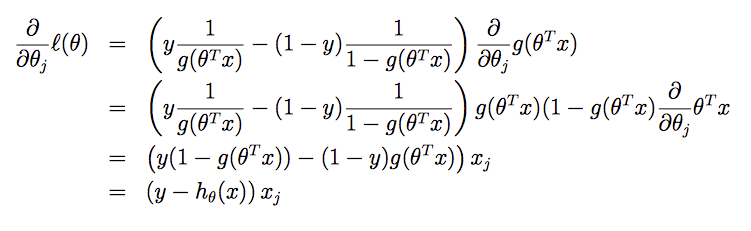
如果有多个样本，同样需要使用梯度算法。但和线性回归有一个区别：为了使函数最大化，要将之前更新算法中的 “-“ 改为“+“，“下降“改为“上升“。

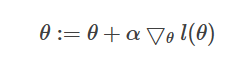
将上面单个训练样本J(θ)的导数进行向量化，得到 随机梯度上升算法 的更新原则（随机没有求和，批量有求和）：

这和上一讲中的最小二乘法更新规则的表达式一样，但是其中 h_θ(x) 却不同。最小二乘法中的 h_θ(x) 是线性函数，而此表达式中的 h_θ(x) 是sigmoid函数。

3.2 Newton’s method 牛顿方法

极值点就是导数为0的地方，所以最大化对数似然函数的另一个求法是求对数似然函数导数为0的点。

（1）考虑最简单情况：θ是一个实数，首先找到一个实数域上的方程 f，f(θ)=0。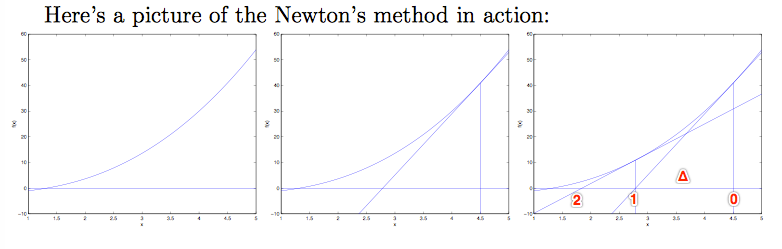

从起始点θ₀开始，找到f(θ₀)处的切线，与坐标轴相交于θ₁。再从求 f(θ₁) 处的切线，与坐标轴相交于θ_2。不断迭代，直到切线斜率为0。

如果将 θ₀ 和 θ₁两点之间的距离记为Δ，可以通过求Δ来判断下一个θ在哪。根据 tan() 的特性，有：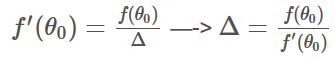

所以牛顿方法执行更新规则：

如果想要找到 θ 使得 l(θ) 最大，那么 θ 满足 l′(θ) = 0，可以将牛顿方法运用其中，将 l′(θ)替代上式中的 f(θ)，得到：

注：如果想要使用牛顿方法最小化而不是最大化一个函数，公式怎么改？答案是不改，因为最小和最大值处对应的导数都是0。
（2）考虑一般化情况，θ 是一个向量。则一般化的牛顿方法(也称作Newton-Raphson method) 为：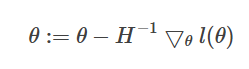

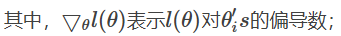
H表示黑塞矩阵(Hessian matrix)，是二阶导数矩阵。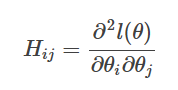

3.2 牛顿方法的优缺点

优点：牛顿方法比梯度上升算法减少了迭代次数，通常来说有更快的收敛速度，相对来说经过很少次迭代就能接近最小值。也称为二次收敛 quadratic conversions，即收敛速度几乎翻倍。

缺点：每次迭代都要重新计算 Hessian矩阵的逆，如果在大规模数据中涉及很多特征，将花费巨大计算代价并且变慢。

Google 是利用逻辑回归预测搜索广告的点击率。

https://blog.csdn.net/TRillionZxY1/article/details/77099955