Cross Entropy in Machine Learning

整理摘自：https://blog.csdn.net/tsyccnh/article/details/79163834

信息论

Outline

1. 信息量与信息熵

2. 相对熵（KL散度）

3. 交叉熵

--------------------------------

1. 信息量与信息熵

https://baike.baidu.com/item/%E4%BF%A1%E6%81%AF%E7%86%B5/7302318?fr=aladdin

　　信息论之父 C. E. Shannon 在 1948 年发表的论文“通信的数学理论（ A Mathematical Theory of Communication ）”中， Shannon 指出，任何信息都存在冗余，冗余大小与信息中每个符号（数字、字母或单词）的出现概率或者说不确定性有关。香农用信息熵的概念来描述信源的不确定度。

　　通常，一个信源发送出什么符号是不确定的，衡量它可以根据其出现的概率来度量。概率大，出现机会多，不确定性小；反之就大。

　　(1) 某一单个符号发生的不确定性

　　假设X是一个离散型随机变量，其取值集合为χ,概率分布函数p(x)=Pr(X=x),x∈χ,则定义事件X=x0的信息量为：

　　I(x₀) = −log(p(x₀))

　　(2) 信源所有可能发生情况的平均不确定性

　　在信源中，考虑的不是某一单个符号发生的不确定性，而是要考虑这个信源所有可能发生情况的平均不确定性。若信源符号有n种取值：U₁…U_i…U_n，对应概率为：P₁…P_i…P_n，且各种符号的出现彼此独立。这时，信源的平均不确定性应当为单个符号不确定性 -logP_i的统计平均值（E），可称为信息熵，即

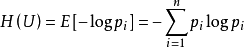式中对数一般取2为底，单位为比特。也可以取其它对数底，采用其它相应的单位，它们间可用换底公式换算。

例子：假设你拿出了你的电脑，按下开关，会有三种可能性，下表列出了每一种可能的概率及其对应的信息量

序号	事件	概率p	信息量I
A	电脑正常开机	0.7	-log(p(A))=0.36
B	电脑无法开机	0.2	-log(p(B))=1.61
C	电脑爆炸了	0.1	-log(p(C))=2.30

熵用来表示所有信息量的期望，上面的问题结果就是

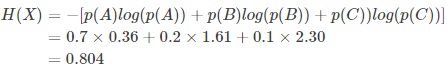
　　(3) 0-1分布问题

　　对于这类问题，熵的计算方法可以简化为：

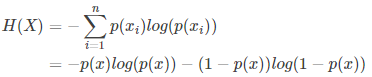
2. 相对熵（KL散度）

　　相对熵又称KL散度,如果我们对于同一个随机变量 x 有两个单独的概率分布 P(x) 和 Q(x)，我们可以使用 KL 散度（Kullback-Leibler (KL) divergence）来衡量这两个分布的差异。

　　维基百科对相对熵的定义：

　　In the context of machine learning, DKL(P‖Q) is often called the information gain achieved if P is used instead of Q.

即如果用P来描述目标问题，而不是用Q来描述目标问题，得到的信息增量。

　　在机器学习中，P往往用来表示样本的真实分布，比如[1,0,0]表示当前样本属于第一类。Q用来表示模型所预测的分布，比如[0.7,0.2,0.1]。
　　直观的理解就是如果用P来描述样本，那么就非常完美。而用Q来描述样本，虽然可以大致描述，但是不是那么的完美，信息量不足，需要额外的一些“信息增量”才能达到和P一样完美的描述。如果我们的Q通过反复训练，也能完美的描述样本，那么就不再需要额外的“信息增量”，Q等价于P。

　　KL散度的计算公式：

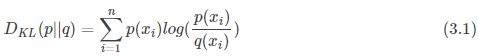
　　n为事件的所有可能性，D_KL 的值越小，表示q分布和p分布越接近。

附注：这里 p(x_i) / q(x_i) 在一定程度上可以衡量p,q之间的差距。当 p = q 时，商为1，log值为0，D_KL= 0.

3. 交叉熵

　　对式3.1变形可以得到：

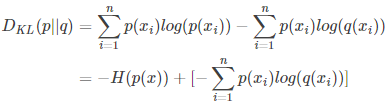
　　等式的前一部分恰巧就是p的熵，等式的后一部分，就是交叉熵：

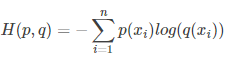
　　在机器学习中，我们需要评估label和predicts之间的差距，使用KL散度刚刚好，即，由于KL散度中的前一部分−H(y)不变，故在优化过程中，只需要关注交叉熵就可以了。所以一般在机器学习中直接用用交叉熵做loss，评估模型。

机器学习中交叉熵的应用

Outline

1. 为什么要用交叉熵做loss函数？

2. 交叉熵在单分类问题中的使用

3. 交叉熵在多分类问题中的使用

-------------------------------------------------------------

1. 为什么要用交叉熵做loss函数？

　　在线性回归问题中，常常使用MSE（Mean Squared Error）作为loss函数，比如：

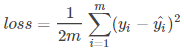
　　这里的m表示m个样本的，loss为m个样本的loss均值。
　　MSE在线性回归问题中比较好用，那么在逻辑分类问题中还是如此么？

2. 交叉熵在单分类问题中的使用

　　这里的单类别是指，每一张图像样本只能有一个类别，比如只能是狗或只能是猫。

　　上式为一张样本的loss计算方法。式2.1中n代表着n种类别。
　　举例说明,比如有如下样本

　　对应的标签和预测值

*	猫	青蛙	老鼠
Label	0	1	0
Pred	0.3	0.6	0.1

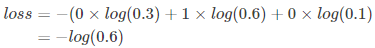
　　对应一个batch的loss就是：

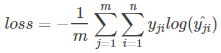
　　m为当前batch的样本数，n为类别数。

3. 交叉熵在多分类问题中的使用

　　这里的多类别是指，每一张图像样本可以有多个类别，比如同时包含一只猫和一只狗。和单分类问题的标签不同，多分类的标签是n-hot。比如下面这张样本图，即有青蛙，又有老鼠，所以是一个多分类问题。

　　对应的标签和预测值：

*	猫	青蛙	老鼠
Label	0	1	1
Pred	0.1	0.7	0.8

　　值得注意的是，这里的Pred不再是通过softmax计算的了，这里采用的是sigmoid。将每一个节点的输出归一化到[0,1]之间。所有Pred值的和也不再为1。换句话说，就是每一个Label都是独立分布的，相互之间没有影响。所以交叉熵在这里是单独对每一个节点进行计算，每一个节点只有两种可能值，所以是一个二项分布。前面说过对于二项分布这种特殊的分布，熵的计算可以进行简化。

附注：相当于对于每一个类别，看做一个0-1分布问题，求各个类别下的loss_i，然后将各个类别的loss加和即为多分类任务总的loss.

　　同样的，交叉熵的计算也可以简化，即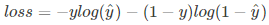

　　注意，上式只是针对一个节点的计算公式。这一点一定要和单分类loss区分开来。
　　例子中可以计算为：

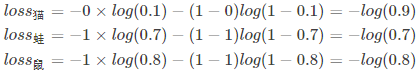
　　单张样本的loss即为

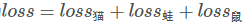
　　每一个batch的loss就是：

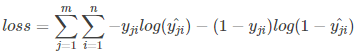
　　式中m为当前batch中的样本量，n为类别数。