洛谷P4724 【模板】三维凸包

题面

传送门

题解

先理一下关于立体几何的基本芝士好了……顺便全都是从\(xzy\)巨巨的博客上抄来的

加减

三维向量加减和二维向量一样

模长

\(|a|=\sqrt{x^2+y^2+z^2}\)

点积

两个向量\(a,b\)的点积还是代表\(a\)在\(b\)上的投影长\(\times b\)的模长，也有$a\cdot b=|a||b|\cos<a,b> \(，坐标上有\)(x_1,y_1,z_1)\cdot (x_2,y_2,z_2)=(x_1x_2,y_1y_2,z_1z_2)$

叉积

是一个三维向量，其模长表示这两个三维向量形成的平行四边形的面积，坐标表示为\((y_1z_2-z_1y_2,z_1x_2-x_1z_2,x_1y_2-y_1x_2)\)

关于叉积的方向，借（dao）用（yong）一下\(xzy\)巨巨的图

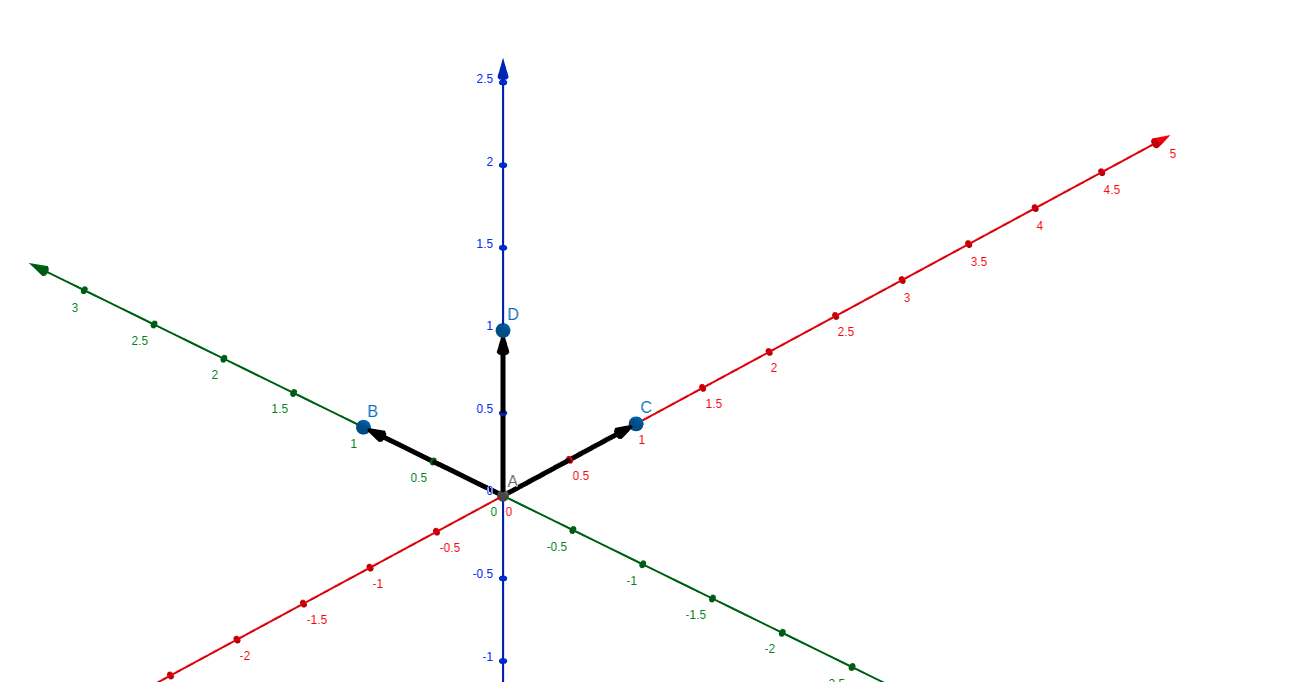
对于\(a\times b\)，伸出右手，食指指向\(a\)，中指指向\(b\)，大拇指所对的方向为叉积后的向量方向，如图中\(AD\)即为\(AC\times AB\)

法向量

指和一个平面垂直的向量，记为\(n\)，显然\(n\)有无数个

任取平面上两个向量做叉积即可

判断点\(P\)是否在平面上

任取平面上一点\(A\)，如果\(n\)和\(AP\)点积为\(0\)说明\(P\)在该平面上

点\(P\)到平面的距离

任取平面上一点\(A\)，那么这个距离实际上就等于\(AP\)在\(n\)上的投影的长度，那么\(AP\)点积\(n\)再除以\(|n|\)即可

求凸包

为了避免四点共面的情况先扰动一下，假装现在每一个面最多只有三个点

维护凸包的时候我们维护凸包的每一个面，把这个面的所有点按逆时针排序

假设我们现在要新增一个点\(P\)，那么从\(P\)向之前的凸包做投影

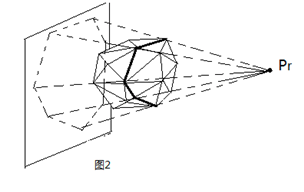
然后把所有能看得到的面都删掉，加入新的面就行了

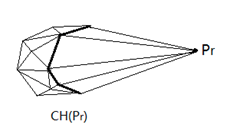
复杂度\(O(n^2)\)

ps：关于复杂度的计算，首先有欧拉公式\(V-E+F=2\)，其中\(V\)为点数，\(E\)为边数，\(F\)为面数，凸包上最多有\(n\)个点，而且易发现有\(3F=2E\)，解得\(F=2n-4,E=3n-6\)。增量法的复杂度是\(V\times E=O(n^2)\)

//minamoto
#include<bits/stdc++.h>
#define R register
#define fp(i,a,b) for(R int i=(a),I=(b)+1;i<I;++i)
#define fd(i,a,b) for(R int i=(a),I=(b)-1;i>I;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
using namespace std;
char buf[1<<21],*p1=buf,*p2=buf;
inline char getc(){return p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++;}
int read(){
    R int res,f=1;R char ch;
    while((ch=getc())>'9'||ch<'0')(ch=='-')&&(f=-1);
    for(res=ch-'0';(ch=getc())>='0'&&ch<='9';res=res*10+ch-'0');
    return res*f;
}
double readdb()
{
    R double x=0,y=0.1,f=1;R char ch;
    while((ch=getc())>'9'||ch<'0')(ch=='-')&&(f=-1);
    for(x=ch-'0';(ch=getc())>='0'&&ch<='9';x=x*10+ch-'0');
    for(ch=='.'&&(ch=getc());ch>='0'&&ch<='9';x+=(ch-'0')*y,y*=0.1,ch=getc());
    return x*f;
}
const int N=2005;const double eps=1e-8;
inline double Rd(){return 1.0*rand()/RAND_MAX;}
inline double reps(){return (Rd()-0.5)*eps;}
struct point{
	double x,y,z;
	point(){}
	point(R double xx,R double yy,R double zz):x(xx),y(yy),z(zz){}
	inline void init(){x=readdb()+reps(),y=readdb()+reps(),z=readdb()+reps();}
	inline point operator -(const point &b)const{return point(x-b.x,y-b.y,z-b.z);}
	inline point operator *(const point &b)const{return point(y*b.z-z*b.y,z*b.x-x*b.z,x*b.y-y*b.x);}
	inline double operator ^(const point &b)const{return x*b.x+y*b.y+z*b.z;}
	inline double norm()const{return sqrt(x*x+y*y+z*z);}
}p[N];
struct node{
	int id[3];
	node(){}
	node(R int x,R int y,R int z){id[0]=x,id[1]=y,id[2]=z;}
	inline point normal(){return (p[id[1]]-p[id[0]])*(p[id[2]]-p[id[0]]);}
	inline double area(){return normal().norm()/2;}
	inline bool ck(const point &b){return ((b-p[id[0]])^normal())>0;}
}f[N*3],st[N*3];
int vis[N][N],n,top,cnt,v;double res;
void Convex_3D(){
	f[++cnt]=node(1,2,3),f[++cnt]=node(3,2,1);
	fp(i,4,n){
		top=0;
		fp(j,1,cnt){
			v=f[j].ck(p[i]),!v?(st[++top]=f[j],0):0;
			vis[f[j].id[0]][f[j].id[1]]=
			vis[f[j].id[1]][f[j].id[2]]=
			vis[f[j].id[2]][f[j].id[0]]=v;
		}
		fp(j,1,cnt){
			if(vis[f[j].id[0]][f[j].id[1]]&&!vis[f[j].id[1]][f[j].id[0]])st[++top]=node(i,f[j].id[0],f[j].id[1]);
			if(vis[f[j].id[1]][f[j].id[2]]&&!vis[f[j].id[2]][f[j].id[1]])st[++top]=node(i,f[j].id[1],f[j].id[2]);
			if(vis[f[j].id[2]][f[j].id[0]]&&!vis[f[j].id[0]][f[j].id[2]])st[++top]=node(i,f[j].id[2],f[j].id[0]);
		}
		fp(j,1,top)f[j]=st[j];cnt=top;
	}
	fp(i,1,cnt)res+=f[i].area();
	printf("%.3lf\n",res);
}
int main(){
//	freopen("testdata.in","r",stdin);
	n=read();
	fp(i,1,n)p[i].init();
	Convex_3D();
	return 0;
}