logistic回归和线性回归

1.输出：

线性回归输出是连续的、具体的值（如具体房价123万元） 回归

逻辑回归的输出是0~1之间的概率，但可以把它理解成回答“是”或者“否”（即离散的二分类）的问题 分类

2.假设函数

线性回归：

θ数量与x的维度相同。x是向量，表示一条训练数据

逻辑回归：增加了sigmoid函数

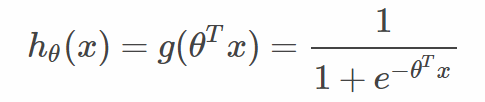
逻辑斯蒂回归是针对线性可分问题的一种易于实现而且性能优异的分类模型，是使用最为广泛的分类模型之一。

sigmoid函数来由

假设某件事发生的概率为p，那么这件事不发生的概率为(1-p)，我们称p/(1-p)为这件事情发生的几率。取这件事情发生几率的对数，定义为logit(p)，所以logit(p)为

 

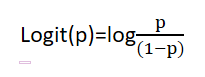
因为logit函数的输入取值范围为[0,1](因为p为某件事情发生的概率)，所以通过logit函数可以将输入区间为[0,1]转换到整个实数范围内的输出,log函数图像如下

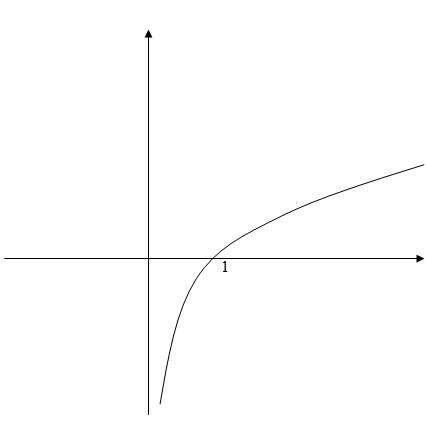
将对数几率记为输入特征值的线性表达式如下：

其中,p(y=1|x)为，当输入为x时，它被分为1类的概率为h_θ(x)，也属于1类别的条件概率。而实际上我们需要的是给定一个样本的特征输入x，而输出是一个该样本属于某类别的概率。所以，我们取logit函数的反函数，也被称为logistic函数也就是sigmoid函数

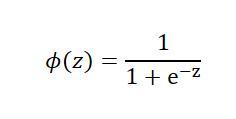
ϕ(z)中的z为样本特征与权重的线性组合（即前面的Θ^Tx）。通过函数图像可以发现sigmoid函数的几个特点，

当z趋于正无穷大的时候，ϕ(z)趋近于1，因为当z趋于无穷大的时候，e^(-z)趋于零，所以分母会趋于1，

当z趋于负无穷大的时候，e^(-z)会趋于正无穷大，所以ϕ(z)会趋于0。

如在预测天气的时候，我们需要预测出明天属于晴天和雨天的概率，已知根天气相关的特征和权重，定义y=1为晴天，y=-1为雨天，根据天气的相关特征和权重可以获得z，然后再通过sigmoid函数可以获取到明天属于晴天的概率ϕ(z)=P(y=1|x)，如果属于晴天的概率为80%，属于雨天的概率为20%，那么当ϕ(z)>=0.8时，就属于雨天，小于0.8时就属于晴天。

我们可以通过以往天气的特征所对应的天气，来求出权重和ϕ(z)的阈值，也就是天气所说的0.8。

逻辑斯蒂回归除了应用于天气预测之外，还可以应用于某些疾病预测，所以逻辑斯蒂回归在医疗领域也有广泛的应用。

3.目标函数

线性回归  最小二乘法（Least squears）的成本函数（Cost function） 求最小

逻辑回归 似然函数 目标函数l(θ)即J(θ) 求最大

逻辑斯蒂回归中所定义的代价函数就是使得该件事情发生的几率最大，也就是某个样本属于其真实标记样本的概率越大越好

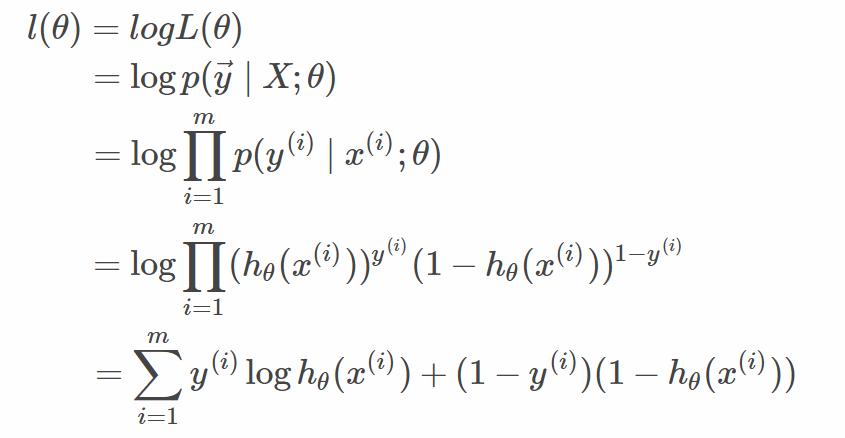
4.求解方法

线性回归  最小二乘--梯度下降 或者用矩阵方程

逻辑回归  极大似然--梯度上升 或者牛顿法

5.逻辑回归可以从广义线性模型推倒出来

logistic回归本质上是线性的，因为它只是在特征到结果的映射中加入了一个sigmoid函数。

即先把特征求和，然后使用非线性的函数将连续值映射到0与1之间。

损失函数

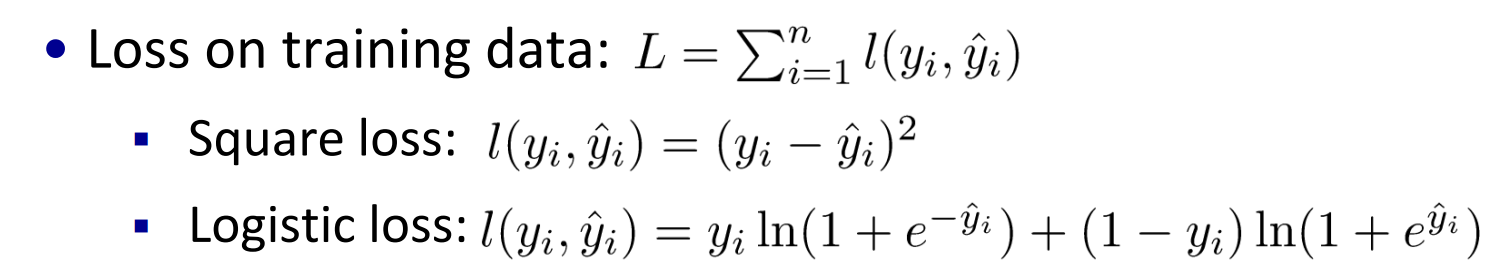
对应logistic regression， 由以上表征正确的概率含义可知，我们希望其值越大，模型对数据的表达能力越好。而我们在参数更新或衡量模型优劣时是需要一个能充分反映模型表现误差的损失函数（Loss function）或者代价函数（Cost function）的，而且我们希望损失函数越小越好。由这两个矛盾，那么我们不妨领代价函数为上述组合对数概率的相反数：

上式即为大名鼎鼎的交叉熵损失函数。(说明：如果熟悉“信息熵“的概念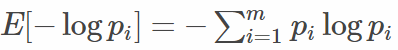，那么可以有助理解叉熵损失函数）

权值更新

线性回归

1.梯度下降算法

对于线性回归问题，我们需要解决的事情往往如下：

定义出Cost Function -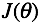 

希望能够找到一组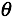，能够最小化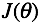，即

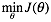
梯度下降算法步骤如下：

1. 随机选择一组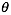

2. 不断的变化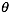，让变小

j=0,1,...n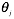，是所有n+1个值同时进行变化。α 是代表学习速率。 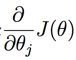是Cost Function对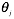的偏导数。

3. 直到寻找到最小值

偏导求解如下：

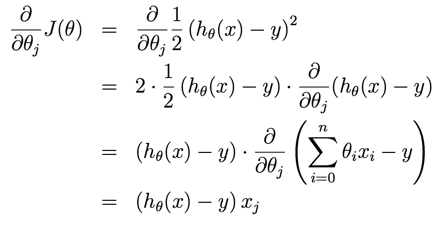
因此最终的梯度下降算法表达如下：

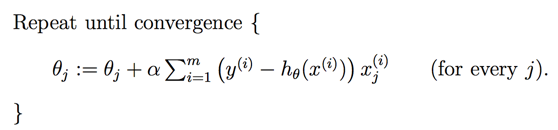
2.正规方程Normal Equation

梯度下降算法给出了一种方法可以最小化Cost Function。正规方程（Normal Equation）是另外一种方法，它使用非常直接的方式而不需要进行迭代的算法。在这个方法中，我们通过对J取对应的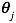的偏导数，然后将偏导数设置为0。通过推导，正规方程如下：

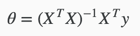
梯度下降算法和正规方程对比如下：

梯度下降算法	正规方程
需要选择学习速率参数	不需要学习速率参数
需要很多次迭代	不需要迭代
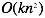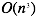n如果很大依旧还能工作	n如果很大，速度会非常慢

logistic回归

因为各个观测样本之间相互独立，那么它们的联合分布为各边缘分布的乘积。得到似然函数为

然后我们的目标是求出使这一似然函数的值最大的参数估计，最大似然估计就是求出参数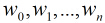，使得

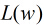
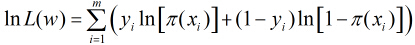
取得最大值，对函数取对数得到

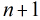
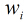
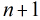
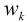
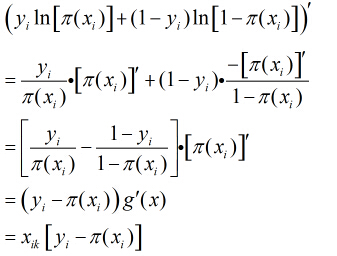
继续对这个分别求偏导，得到个方程，比如现在对参数求偏导，由于

所以得到

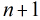
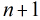
这样的方程一共有个，所以现在的问题转化为解这个方程形成的方程组。

上述方程比较复杂，一般方法似乎不能解之，所以我们引用了牛顿-拉菲森迭代方法求解。

也可以利用牛顿迭代求多元函数的最值问题

简单牛顿迭代法：http://zh.m.wikipedia.org/wiki/%E7%89%9B%E9%A1%BF%E6%B3%95

实际上在上述似然函数求最大值时，可以用梯度上升算法，一直迭代下去。梯度上升算法和牛顿迭代相比，收敛速度

慢，因为梯度上升算法是一阶收敛，而牛顿迭代属于二阶收敛。

交叉熵代价函数(损失函数)及其求导推导

Logistic 回归模型的参数估计为什么不能采用最小二乘法？

Logistic回归原理及公式推导

彻底搞懂逻辑斯蒂回归