Deep Learning 学习笔记（1）：线性回归( Linear Regression )

关于DL，由于我是零经验入门，

事实上我是从最简单的ML开始学起，

所以这个系列我也从ML开始讲起。

===============并行分割线=================

一、线性回归

线性回归主要运用于“预测”类问题：

假设我们有一堆的数据（房间大小，房价）。给定一个没见过的房间大小，它的价格应该怎么估计呢？

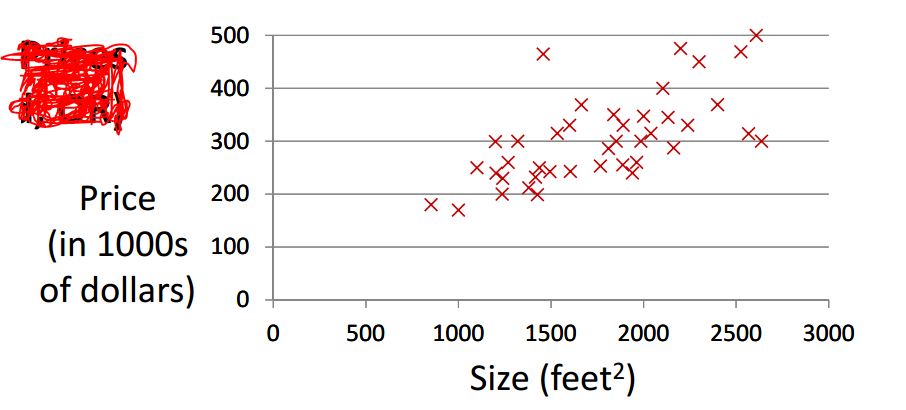
一般来说，我们可以假定房价h(x)和大小x之间存在一种线性关系。求出最优h(x)后，

对于每一个大小x的房间，我们都可以给出一个估价h(x)

概念：COST FUNCTION（代价函数）

给定假设h(x):

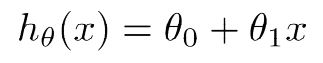
在已知数据的条件下，他的代价函数为J(theta1,theta2):

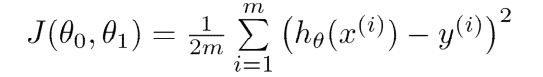
可见，代价函数体现了一种预测值与实际值之间的误差（欧式距离的均值）

而我们的目标——

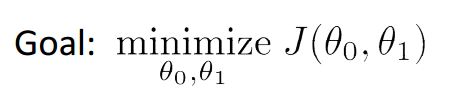
二、Gradient Descent（梯度下降）

梯度下降是一种在已知数据中求解最优h(x)的方法。

核心步骤：

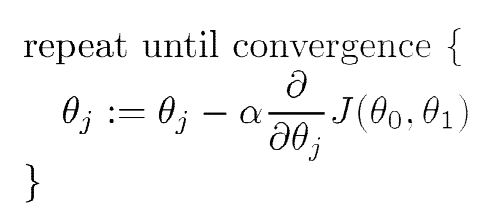
注意：必须在求的所有参数之后同时更新，才能进行下一次循环

原理：

对于一个碗型函数，每进行一次参数更新，都会是取值更加接近最优解（碗底）

以二次函数为例，看起来大概就是这个样子

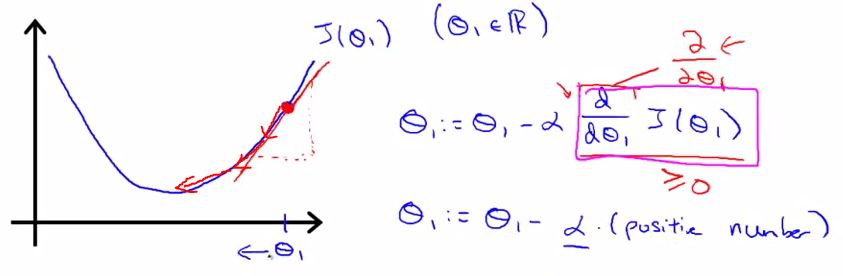
其中alpha称为学习速率(learning rate)，过大将会使算法 不能收敛， 过小则收敛过慢

对于有两个参数的单价函数的梯度下降，其收敛过程看起来大概就是这个样子（注意，可以有两种不同路径）

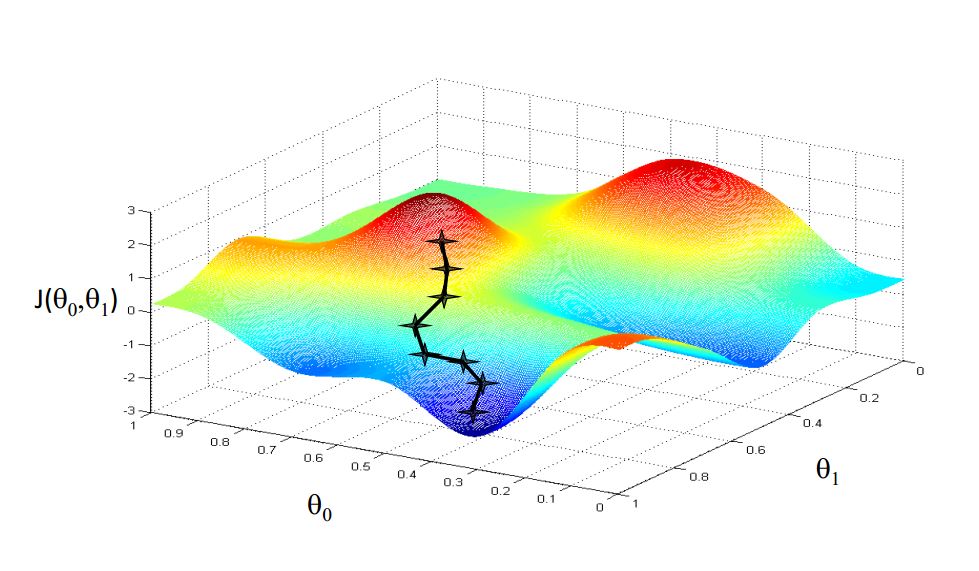
通过不断进行梯度下降，我们可以求得给定数据下的参数的局部最优解

（数学没学好，表述很垃圾，最近准备重学线性代数）

因此，整个线性回归过程可以总结如下：

1、根据给定数据架设预测函数h(x)

2、计算代价函数J

3、计算各参数偏导

4、更新参数

5、重复2~4直到代价函数跟新的步长小于设定值或者是重复次数达到预设值。