洛谷 P3397 地毯 【二维差分标记】

题目背景

此题约为NOIP提高组Day2T1难度。

题目描述

在n*n的格子上有m个地毯。

给出这些地毯的信息，问每个点被多少个地毯覆盖。

输入输出格式

输入格式：

第一行，两个正整数n、m。意义如题所述。

接下来m行，每行两个坐标(x1,y1)和(x2,y2)，代表一块地毯，左上角是(x1,y1)，右下角是(x2,y2)。

输出格式：

输出n行，每行n个正整数。

第i行第j列的正整数表示(i,j)这个格子被多少个地毯覆盖。

输入输出样例

输入样例#1：

5 3

2 2 3 3

3 3 5 5

1 2 1 4

输出样例#1：

0 1 1 1 0

0 1 1 0 0

0 1 2 1 1

0 0 1 1 1

0 0 1 1 1

说明

样例解释

0 0 0 0 0 0 0 0 0 0 0 1 1 1 0

0 1 1 0 0 0 1 1 0 0 0 1 1 0 0

0 1 1 0 0 -> 0 1 2 1 1 -> 0 1 2 1 1

0 0 0 0 0 0 0 1 1 1 0 0 1 1 1

0 0 0 0 0 0 0 1 1 1 0 0 1 1 1

数据范围

对于20%的数据，有n<=50，m<=100。

对于100%的数据，有n<=1000，m<=1000。

【題意】：略

【分析】：//by阮行止

n*n的矩阵，每次给一个子矩阵 区间+1 。最后输出整个矩阵。

优化。用二维线段树或二维树状数组完成上面的操作。

足以吊打此题。

但是NOIP是不会考二维数据结构的

考虑这个问题的一维版：一个序列，最开始全是 0 .每次区间加 1 ,最后输出每个数。

于是有一种叫做“差分”的奇技淫巧：

假设我们现在要给[2,5]这个区间加一。原来的序列是：

0 0 0 0 0 0 0 0

这时候我们在2上面打 +1 标记， 6 上面打 -1 标记。那么现在的序列是：

0 +1 0 0 0 -1 0

有什么用呢？从左往右扫描这个数组，记录当前经过的标签之和。这个和就是对应那个数的答案。

这样，对于每个区间加操作，只需要O(1) 的时间打上标记。

最后扫描输出即可。

现在把问题拓展到二维。假设我们要覆盖[(2,2),(5,5)] ，那么标记便可以这样打：

0 0 0 0 0 0
0 +1 0 0 0 -1
0 +1 0 0 0 -1
0 +1 0 0 0 -1
0 +1 0 0 0 -1
0 0 0 0 0 0
即在每一行都按照一维的方式来操作

int sum=0,i,j;
   for(i=1;i<=n+1;i++)
      for(j=1;j<=n+1;j++)
         sum+=flag[i][j],real[i][j]=sum;
之后 real 数组里就存了最后的矩阵。输出即可。

这个算法的复杂度是每次打标记O(n) ，总复杂度是O(mn+n^2)

【代碼】：[一維]

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<vector>
#include<queue>
#include<map>
#include<set>
#include<ctime>
//#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
int a[1005][1005];
int x[1005][1005];
const int maxn=1e5+10;
void fun(int x1,int y1,int x2, int y2)
{
    for(int i=x1; i<=x2; i++)
    {
        for(int j=y1; j<=y2; j++)
        {
            a[i][j]++;
        }
    }
}
int main()
{
    int n,m;
    while(~scanf("%d%d",&n,&m))
    {
        int x1,y1,x2,y2;
        memset(a,0,sizeof(a));
        while(m--)
        {
            scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
            for(int i=x1;i<=x2;i++)
            {
                a[i][y1]++;
                a[i][y2+1]--;
            }
        }
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=n;j++)
            {
                x[i][j] = x[i][j-1] + a[i][j];
                printf("%d ",x[i][j]);
            }
            printf("\n");
        }
    }
}
/*
5 3
2 2 3 3
3 3 5 5
1 2 1 4

0 1 1 1 0
0 1 1 0 0
0 1 2 1 1
0 0 1 1 1
0 0 1 1 1

0 0 0 0 0         0 0 0 0 0        0 1 1 1 0
0 1 1 0 0         0 1 1 0 0        0 1 1 0 0
0 1 1 0 0    ->   0 1 2 1 1   ->   0 1 2 1 1
0 0 0 0 0         0 0 1 1 1        0 0 1 1 1
0 0 0 0 0         0 0 1 1 1        0 0 1 1 1

*/

首先这题的主要思想很多大佬都讲了：就是差分，但是我的写法和他们的写法又不一样。

本题数据范围为n<=1000,m<=1000。

当n<=1000,m<=1000000甚至m<=10000000怎么办呢？

这时不管是O(n)的修改，还是甚至是 O(log^2(n))O(log
2
 (n)) ，都是跑不过的。

而我们有一个O(1)修改的做法：二维差分。

设b[i][j]=a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1]。

这样每次修改b[i][j]相当于对任意 i\le x,j \le yi≤x,j≤y 对a[x][y]做同样的修改

然后每次修改就直接++b[x1][y1],--b[x2+1][y1],--b[x1][y2+1],++b[x2+1][y2+1]即可。

也就是用 O(1)O(1) 的复杂度表示 O(n^2)O(n
2
 ) 的覆盖（原话来自下面那篇题解“用O(1)复杂度来表示O(N)的覆盖”）

最后再直接a[i][j]=a[i-1][j]+a[i][j-1]-a[i-1][j-1]+b[i][j]还原出原序列即可。

/* Author: CNYALI_LK

LANG: C++

PROG: 3397.cpp

*/

[二維]

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<vector>
#include<queue>
#include<map>
#include<set>
#include<ctime>
//#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
int a[1005][1005];
int x[1005][1005];
const int maxn=1e5+10;

int main()
{
    int n,m;
    while(~scanf("%d%d",&n,&m))
    {
        int x1,y1,x2,y2;
        memset(a,0,sizeof(a));
        while(m--)
        {
            scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
            a[x1][y1]++; //
            a[x2+1][y1]--;
            a[x1][y2+1]--; //
            a[x2+1][y2+1]++;

        }
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=n;j++)
            {
                a[i][j] += a[i-1][j] + a[i][j-1] - a[i-1][j-1];
                printf("%d%c",a[i][j],j==n?'\n':' ');
            }
        }
    }
}

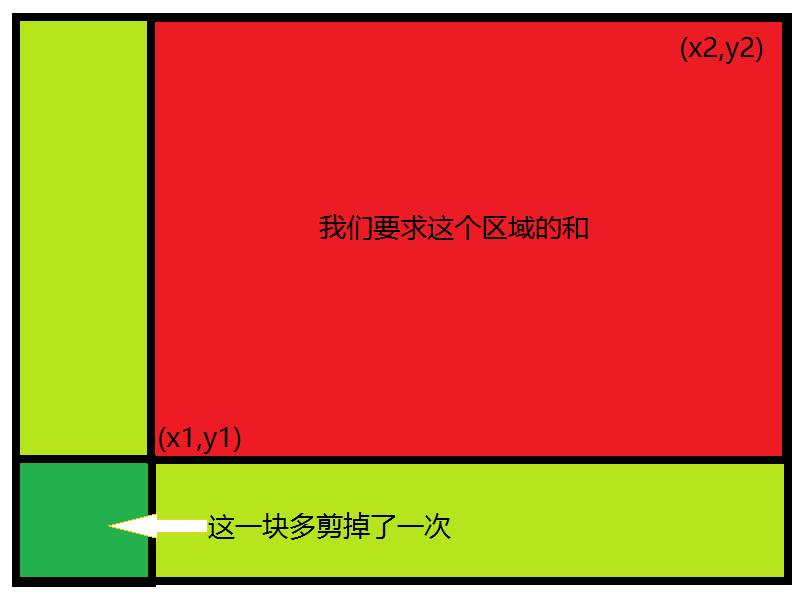
我们借助这个图片研究一下。假设在这个矩阵（二维数组）中，我们要求和的是上图中红色区域。现在我们已经预处理出了所有点的前缀和，现在给定两个点（x1,y1），（x2,y2），我们要求 以这两个点连线为对角线的一个子矩阵的数值之和。暴力做法直接挨个加这个我就不再多说了，反正早晚都得TLE，我们重点考虑用前缀和的快速做法。

首先我们可以把s[x2][y2]求出来，它代表整个大矩形的前缀和，然后我们分别减去它左边多出来的一块的前缀和和下边多出来一块的前缀和，这样就是最终答案了？

不是！这不是最终答案。可以发现，在我们剪掉这两个多出的区域时，下边的一小块被减了两次，但减两次显然是不合理的，我们应该加回来。。

所以对于一次的查询答案ans应该等于s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]。

这个二维前缀和也称差分序列。