HDU4940 Destroy Transportation system(有上下界的最大流)

Problem Description

Tom is a commander, his task is destroying his enemy’s transportation system.

Let’s represent his enemy’s transportation system as a simple directed graph G with n nodes and m edges. Each node is a city and each directed edge is a directed road. Each edge from node u to node v is associated with two values D and B, D is the cost to destroy/remove such edge, B is the cost to build an undirected edge between u and v.

His enemy can deliver supplies from city u to city v if and only if there is a directed path from u to v. At first they can deliver supplies from any city to any other cities. So the graph is a strongly-connected graph.

He will choose a non-empty proper subset of cities, let’s denote this set as S. Let’s denote the complement set of S as T. He will command his soldiers to destroy all the edges (u, v) that u belongs to set S and v belongs to set T.

To destroy an edge, he must pay the related cost D. The total cost he will pay is X. You can use this formula to calculate X: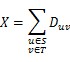

After that, all the edges from S to T are destroyed. In order to deliver huge number of supplies from S to T, his enemy will change all the remained directed edges (u, v) that u belongs to set T and v belongs to set S into undirected edges. (Surely, those edges exist because the original graph is strongly-connected)

To change an edge, they must remove the original directed edge at first, whose cost is D, then they have to build a new undirected edge, whose cost is B. The total cost they will pay is Y. You can use this formula to calculate Y: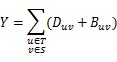

At last, if Y>=X, Tom will achieve his goal. But Tom is so lazy that he is unwilling to take a cup of time to choose a set S to make Y>=X, he hope to choose set S randomly! So he asks you if there is a set S, such that Y<X. If such set exists, he will feel unhappy, because he must choose set S carefully, otherwise he will become very happy.

 

Input

There are multiply test cases.

The first line contains an integer T(T<=200), indicates the number of cases.

For each test case, the first line has two numbers n and m.

Next m lines describe each edge. Each line has four numbers u, v, D, B. 
(2=<n<=200, 2=<m<=5000, 1=<u, v<=n, 0=<D, B<=100000)

The meaning of all characters are described above. It is guaranteed that the input graph is strongly-connected.

 

Output

For each case, output "Case #X: " first, X is the case number starting from 1.If such set doesn’t exist, print “happy”, else print “unhappy”.

 

Sample Input

2

3 3

1 2 2 2

2 3 2 2

3 1 2 2

3 3

1 2 10 2

2 3 2 2

3 1 2 2

 

Sample Output

Case #1: happy

Case #2: unhappy

同上一道题，不过在我不知道这题要用最大流来做的情况下我是不会想到的：

关键是要构造出不等式，而且把不等式对应到可行流。

#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=4;
const int inf=;
int Laxt[maxn],Next[maxn],To[maxn],Cap[maxn],cnt;
int dis[maxn],nd[maxn],S,T,num,ans,q[maxn],qnum[maxn],top;
void init()
{
    cnt=;ans=num=top=;
    memset(Laxt,,sizeof(Laxt));
    memset(dis,,sizeof(dis));
    memset(nd,,sizeof(nd));
}
int add(int u,int v,int c)
{
    Next[++cnt]=Laxt[u];
    Laxt[u]=cnt;
    To[cnt]=v;
    Cap[cnt]=c;

    Next[++cnt]=Laxt[v];
    Laxt[v]=cnt;
    To[cnt]=u;
    Cap[cnt]=;
}
int sap(int u,int flow)
{
    if(u==T||flow==) return flow;
    int delta=,tmp;
    for(int i=Laxt[u];i;i=Next[i]){
        int v=To[i];
        if(dis[v]+==dis[u]&&Cap[i]>){
            tmp=sap(v,min(Cap[i],flow-delta));
            delta+=tmp;
            Cap[i]-=tmp;
            Cap[i^]+=tmp;
            if(flow==delta||dis[]>=T) return delta;
        }
    }
    nd[dis[u]]--;
    if(nd[dis[u]]==) dis[]=T;
    nd[++dis[u]]++;
    return delta;
}
int main()
{
    int Case,n,i,j,m,u,v,x,y,k=;
    scanf("%d",&Case);
    while(Case--){
        init();
        scanf("%d%d",&n,&m);
        S=;T=n+;
        for(i=;i<=m;i++){
            scanf("%d%d%d%d",&u,&v,&x,&y);
            u++;v++;num+=x;
            add(u,v,y);
            q[++top]=cnt;
            qnum[top]=x;
            add(S,v,x);
            add(u,T,x);
        }
        while(dis[S]<T) {
           ans+=sap(S,inf);
        }
        printf("Case #%d: ",++k);
        if(num!=ans) printf("unhappy\n");
        else printf("happy\n");
    }
    return ;
}

（希望多遇到几个这样的模型，然后好好理解一下）