【bzoj2438】[中山市选2011]杀人游戏 Tarjan

题目描述

一位冷血的杀手潜入 Na-wiat，并假装成平民。警察希望能在 N 个人里面，查出谁是杀手。警察能够对每一个人进行查证，假如查证的对象是平民，他会告诉警察，他认识的人， 谁是杀手， 谁是平民。 假如查证的对象是杀手， 杀手将会把警察干掉。现在警察掌握了每一个人认识谁。每一个人都有可能是杀手，可看作他们是杀手的概率是相同的。问：根据最优的情况，保证警察自身安全并知道谁是杀手的概率最大是多少？

输入

第一行有两个整数 N,M。 
接下来有 M 行，每行两个整数 x,y，表示 x 认识 y（y 不一定认识 x） 。

输出

仅包含一行一个实数，保留小数点后面 6 位，表示最大概率。

样例输入

5 4
1 2
1 3
1 4
1 5

样例输出

0.800000

---

题解

Tarjan

显然只需要查证所有 缩点后入度为0的强连通分量中的任意一个点 即可，即必须查证的人的个数等于入度为0的强连通分量个数。

但是这并不一定是最优解。考虑一种情况：

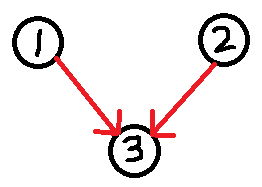
这时只需要查证2（或者查证1）即可，可以不查证1（或2）。

具体原因是：一个入度为0的强连通分量大小为1，如果它指向的所有点都不仅由它到达（即减去它到其的边数后入度不为0），那么可以先查证其它点，直到最后仅剩下这个点，即可不查证该点。

于是需要再统计一下是否有这种情况。具体方法：枚举每个点，判断它所有能够到达的点是否仅由它到达即可。注意这样的点只能保留1个（多了无法排除），因此需要及时终止循环。

最后 (n-必须查证的人)/n 即为存活概率。

时间复杂度$O(n+m)$

#include <cstdio>
#include <algorithm>
#define N 100010
#define M 300010
using namespace std;
int head[N] , to[M] , next[M] , cnt , deep[N] , low[N] , tot , vis[N] , ins[N] , sta[N] , top , bl[N] , si[N] , num , ind[N];
inline void add(int x , int y)
{
	to[++cnt] = y , next[cnt] = head[x] , head[x] = cnt;
}
void tarjan(int x)
{
	int i;
	deep[x] = low[x] = ++tot , vis[x] = ins[x] = 1 , sta[++top] = x;
	for(i = head[x] ; i ; i = next[i])
	{
		if(!vis[to[i]]) tarjan(to[i]) , low[x] = min(low[x] , low[to[i]]);
		else if(ins[to[i]]) low[x] = min(low[x] , deep[to[i]]);
	}
	if(deep[x] == low[x])
	{
		int t;
		num ++ ;
		do
		{
			t = sta[top -- ] , si[num] ++ ;
			ins[t] = 0 , bl[t] = num;
		}while(t != x);
	}
}
bool judge(int x)
{
	int i;
	bool flag = 1;
	for(i = head[x] ; i ; i = next[i]) ind[bl[to[i]]] -- ;
	for(i = head[x] ; i ; i = next[i])
		if(!ind[bl[to[i]]])
			flag = 0;
	for(i = head[x] ; i ; i = next[i]) ind[bl[to[i]]] ++ ;
	return flag;
}
int main()
{
	int n , m , i , x , y , ans = 0;
	scanf("%d%d" , &n , &m);
	for(i = 1 ; i <= m ; i ++ ) scanf("%d%d" , &x , &y) , add(x , y);
	for(i = 1 ; i <= n ; i ++ )
		if(!vis[i])
			tarjan(i);
	for(x = 1 ; x <= n ; x ++ )
		for(i = head[x] ; i ; i = next[i])
			if(bl[x] != bl[to[i]])
				ind[bl[to[i]]] ++ ;
	for(i = 1 ; i <= num ; i ++ )
		if(!ind[i])
			ans ++ ;
	for(i = 1 ; i <= n ; i ++ )
		if(si[bl[i]] == 1 && !ind[bl[i]] && judge(i))
			break;
	if(i <= n) ans -- ;
	printf("%.6lf\n" , (double)(n - ans) / n);
	return 0;
}