玉蟾宫（悬线dp）

求最大子矩阵一般用采用悬线法 (包好用的牢底)

悬线法:

• [ 以这道题为例，我们将R称为障碍格子，将F称为非障碍格子]

• 我们选择任意一个非障碍格子，引出三条直线：左直 右直 上直
  
  

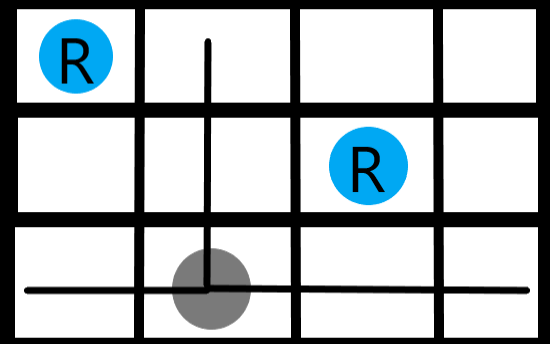
• 随后从这个点出发，分别向上 左 右延申直到遇到障碍格

我们要求上悬线尽可能高的面积, 但有可能上一层的左直线比这一层短，所以不能直接傻傻地用上*（右-左+1）；

所以要让左悬线尽可能大，右悬线尽可能小

最后轮流求每个非障碍点能延伸到的最大面积

公主请欣赏代码

#include<bits/stdc++.h>
using namespace std;

const int N = 1e3+10;
int n, m, ans;
char a[N][N];
int h[N][N], l[N][N], r[N][N];

int main(){
	scanf("%d%d", &n, &m);
	for(int i=1; i<=n; i++){
		for(int j=1; j<=m; j++){
			cin >> a[i][j];
			h[i][j] = 1; l[i][j] = r[i][j] = j;//将悬线都初始化
		}
	}
	for(int i=1; i<=n; i++){
		for(int j=1; j<=m; j++){
			if(a[i][j] == 'F' and a[i][j-1] == 'F') l[i][j] = l[i][j-1];//延伸左悬线
		}
		for(int j=1; j<=m; j++){
			if(a[i][j] == 'F' and a[i-1][j] == 'F') h[i][j] = h[i-1][j] + 1;//延伸上悬线
		}
		for(int j=m; j>=1; j--){
			if(a[i][j] == 'F' and a[i][j+1] == 'F') r[i][j] = r[i][j+1];//延伸右悬线
		}
	}
	for(int i=1; i<=n; i++){
		for(int j=1; j<=m; j++){
			if(a[i][j] == 'F' and a[i-1][j] == 'F'){
				l[i][j] = max(l[i][j], l[i-1][j]);
				r[i][j] = min(r[i][j], r[i-1][j]);
			}
			if(a[i][j] == 'F'){
				ans = max(ans, h[i][j] * (r[i][j] - l[i][j] + 1));
			}
		}
	}
	printf("%d", ans*3);
	return 0;
}