Pandas中的常用函数

1. map、apply、applymap

参考：Pandas教程 | 数据处理三板斧——map、apply、applymap详解

在日常的数据处理中，经常会对一个DataFrame进行逐行、逐列和逐元素的操作，对应这些操作，Pandas中的map、apply和applymap可以解决绝大部分这样的数据处理需求。

先生成100行示例数据：

boolean=[True,False]
gender=["男","女"]
color=["white","black","yellow"]
data=pd.DataFrame({
    "height":np.random.randint(150,190,100),
    "weight":np.random.randint(40,90,100),
    "smoker":[boolean[x] for x in np.random.randint(0,2,100)],
    "gender":[gender[x] for x in np.random.randint(0,2,100)],
    "age":np.random.randint(15,90,100),
    "color":[color[x] for x in np.random.randint(0,len(color),100) ]
}
)

1.1 Series数据处理

1. map

若想把数据集中gender列的男替换为1，女替换为0，可使用 Series.map()：

# 法一：使用字典进行映射
data["gender"] = data["gender"].map({"男":1, "女":0})

# 法二：使用函数
def gender_map(x):
    gender = 1 if x == "男" else 0
    return gender
# 注意这里传入的是函数名，不带括号
data["gender"] = data["gender"].map(gender_map)

不论是利用字典还是函数进行映射，map方法都是把对应的数据逐个当作参数传入到字典或函数中，得到映射后的值。

注：若该列中存在map字典中不存在的值，例如，gender 中还存在“未知”，则“未知”会被映射为Nan，此时可选择使用函数进行映射，定义一个else。同时使用函数会更加灵活，例如当满足多个条件时，都映射到某个值

2. apply

apply方法的作用原理和map方法类似，区别在于apply 能够传入功能更为复杂的函数。

假设在数据统计的过程中，年龄age列有较大误差，需要对其进行调整（加上或减去一个值），由于这个加上或减去的值未知，故在定义函数时，需要加多一个参数bias，此时用 map 方法是操作不了的（传入map的函数只能接收一个参数），apply 方法则可以解决这个问题。

def apply_age(x,bias):
    return x+bias

# 以元组的方式传入额外的参数
data["age"] = data["age"].apply(apply_age,args=(-3,))

总而言之，对于Series而言，map可以解决绝大多数的数据处理需求，但如果需要使用较为复杂的函数，则需要用到apply方法。

1.2 DataFrame数据处理

1. apply

对DataFrame而言，apply是非常重要的数据处理方法，它可以接收各种各样的函数（Python内置的或自定义的），处理方式很灵活。

在进行具体介绍之前，首先需要了解一下DataFrame中axis的概念（详见我的另一篇博客数据框操作）

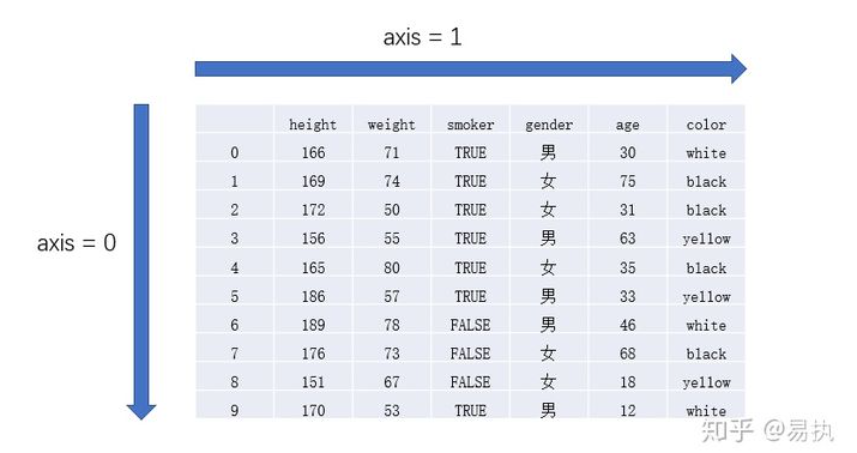
简言之，若想沿着axis=0的方向新增数据，则选择axis=0；若想沿着axis=1的方向新增数据，则选择axis=1。

假设现在需要对data中的数值列分别进行取对数和求和的操作，这时可以用apply进行相应的操作，因为是对列进行操作，所以需要指定axis=0：

# 沿着0轴求和
data[["height","weight","age"]].apply(np.sum, axis=0)

# 沿着0轴取对数
data[["height","weight","age"]].apply(np.log, axis=0)

当沿着轴0（axis=0）进行操作时，会将各列(columns)默认以Series的形式作为参数，传入到你指定的操作函数中，操作后合并并返回相应的结果。

如果在实际使用中需要按行进行操作（axis=1）, 例如：

在数据集中，有身高和体重的数据，所以根据这个我们可以计算每个人的BMI指数（衡量人体肥胖程度和是否健康的重要标准），计算公式是：体重指数BMI=体重/身高的平方（国际单位kg/㎡），因为需要对每个样本进行操作，这里使用axis=1的apply进行操作，代码如下：

def BMI(series):
    weight = series["weight"]
    height = series["height"]/100
    BMI = weight/height**2
    return BMI

data["BMI"] = data.apply(BMI,axis=1)

当apply设置了axis=1对行进行操作时，会默认将每一行数据以Series的形式（Series的索引为列名）传入指定函数，返回相应的结果。

总结一下对 DataFrame 的apply操作：

1. 当axis=0时，对每列columns执行指定函数；当axis=1时，对每行row执行指定函数。
2. 无论axis=0还是axis=1，其传入指定函数的默认形式均为 Series，可以通过设置raw=True传入 numpy数组。
3. 对每个Series执行结果后，会将结果整合在一起返回（若想有返回值，定义函数时需要return相应的值）
4. 当然，DataFrame 的apply和 Series 的apply一样，也能接收更复杂的函数，如传入参数等，实现原理是一样的，具体用法详见官方文档。

2. applymap

applymap的用法比较简单，会对 DataFrame 中的每个单元格执行指定函数的操作

先新生成一个 DataFrame:

df = pd.DataFrame(
    {
        "A":np.random.randn(5),
        "B":np.random.randn(5),
        "C":np.random.randn(5),
        "D":np.random.randn(5),
        "E":np.random.randn(5),
    }
)

现在想将 DataFrame 中所有的值保留两位小数显示，使用applymap可以很快达到这个目的，代码如下：

df.applymap(lambda x:"%.2f" % x)

applymap 将 DataFrame 中的每个数据（每个单元格）作为 x 传入匿名函数

2. groupby

参考：

pandas.DataFrame.groupby — pandas 1.3.0 documentation (pydata.org)

Pandas教程 | 超好用的Groupby用法详解

将数据根据某个或多个字段划分为不同的群体（group）进行分析

例：

先模拟生成10个样本数据：

company=["A","B","C"]

data=pd.DataFrame({
    "company":[company[x] for x in np.random.randint(0,len(company),10)],
    "salary":np.random.randint(5,50,10),
    "age":np.random.randint(15,50,10)
}
)

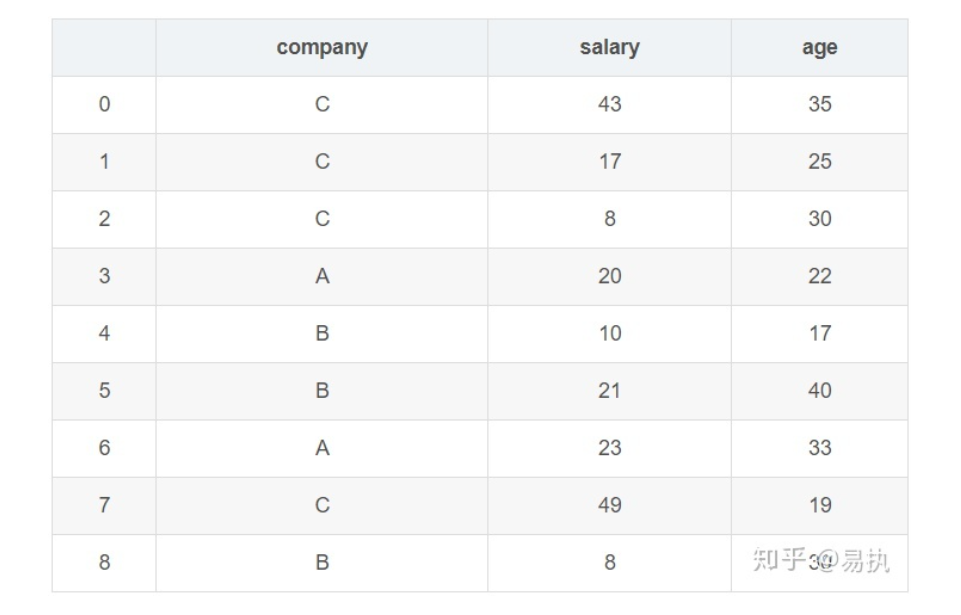
groupby的过程就是将原有的 DataFrame 按照groupby的字段（这里是company），划分为若干个子 DataFrame，在groupby之后的一系列操作（如agg、apply等），均是基于子 DataFrame 的操作。

2.1 agg聚合操作

Pandas中常见的聚合操作：

min, max, sum, mean, median, std, var, count

> data.groupby("company").agg('mean')
         salary    age
company
A         21.50  27.50
B         13.00  29.00
C         29.25  27.25

根据公司进行分组，对其余每一列求平均

> data.groupby("company")["salary"].agg('mean')
         salary    age
company
A         21.50  27.50
B         13.00  29.00
C         29.25  27.25

根据公司进行分组，对 salary 列求平均

> data.groupby('company').agg({'salary':'median','age':'mean'})
         salary    age
company
A          21.5  27.50
B          10.0  29.00
C          30.0  27.25

根据公司进行分组，对 salary 列求中位数，对 age 列求平均

2.2 transform操作

若在求得不同公司员工的平均薪水后，想在原数据集中新增一列avg_salary，该怎么做呢？

不用transform的实现代码如下：

> avg_salary_dict = data.groupby('company')['salary'].mean().to_dict()
> data['avg_salary'] = data['company'].map(avg_salary_dict)
> data
  company  salary  age  avg_salary
0       C      43   35       29.25
1       C      17   25       29.25
2       C       8   30       29.25
3       A      20   22       21.50
4       B      10   17       13.00
5       B      21   40       13.00
6       A      23   33       21.50
7       C      49   19       29.25
8       B       8   30       13.00

如果使用transform，仅需要一行代码：

> data['avg_salary'] = data.groupby('company')['salary'].transform('mean')
> data
  company  salary  age  avg_salary
0       C      43   35       29.25
1       C      17   25       29.25
2       C       8   30       29.25
3       A      20   22       21.50
4       B      10   17       13.00
5       B      21   40       13.00
6       A      23   33       21.50
7       C      49   19       29.25
8       B       8   30       13.00

2.3 apply

apply相比agg和transform而言更加灵活，能够传入任意自定义的函数，实现复杂的数据操作。

假设现在需要获取各个公司年龄最大的员工的数据，可以用以下代码实现：

> def get_oldest_staff(x):
...     df = x.sort_values(by = 'age',ascending=True)
...     return df.iloc[-1,:]
> oldest_staff = data.groupby('company',as_index=False).apply(get_oldest_staff)
> oldest_staff
  company  salary  age
0       A      23   33
1       B      21   40
2       C      43   35

最后，关于apply的使用，虽然说apply拥有更大的灵活性，但apply的运行效率会比agg和transform更慢。所以，groupby之后能用agg和transform解决的问题还是优先使用这两个方法，实在解决不了了才考虑使用apply进行操作。

3. crosstab

参考：Python pandas，分组 groupby()，分组后的聚合函数，交叉表 crosstab()

官方文档：pandas.crosstab — pandas 1.3.0 documentation (pydata.org)

crosstab 交叉表，用于统计分组频率的特殊透视表（列联表）

例：

import pandas as pd

# 模拟用户购买商品的表(数据)
my_list = [{"user_id": 11, "goods": "苹果"}, {"user_id": 11, "goods": "苹果"}, {"user_id": 11, "goods": "香蕉"},
           {"user_id": 22, "goods": "苹果"}, {"user_id": 22, "goods": "香蕉"}, {"user_id": 22, "goods": "香蕉"},
           {"user_id": 33, "goods": "梨"}, {"user_id": 33, "goods": "香蕉"}, {"user_id": 33, "goods": "苹果"}]
df = pd.DataFrame(my_list)
print(df)
'''
  goods     user_id
0    苹果       11
1    苹果       11
2    香蕉       11
3    苹果       22
4    香蕉       22
5    香蕉       22
6     梨        33
7    香蕉       33
8    苹果       33
'''

# 交叉表 (特殊的分组工具)
cross_tb = pd.crosstab(df["user_id"], df["goods"])  # 统计每个用户购买各种商品的数量
print(cross_tb)
'''
goods    梨  苹果  香蕉
user_id
11       0    2    1
22       0    1    2
33       1    1    1
'''
# ↑第一个参数会被放在index

# 如果想得到占比：
pd.crosstab(df["user_id"], df["goods"], normalize="index")
'''
goods          梨       苹果      香蕉
user_id
11       0.000000  0.666667  0.333333
22       0.000000  0.333333  0.666667
33       0.333333  0.333333  0.333333
'''
# ↑ 根据index进行normalize，行相加为1

pd.crosstab(df["user_id"], df["goods"], normalize="columns")
'''
goods     梨   苹果   香蕉
user_id
11       0.0  0.50  0.25
22       0.0  0.25  0.50
33       1.0  0.25  0.25
'''
# ↑ 根据column进行normalize，列相加为1

pd.crosstab(df["user_id"], df["goods"], normalize="all")
'''
goods           梨      苹果       香蕉
user_id
11       0.000000  0.222222  0.111111
22       0.000000  0.111111  0.222222
33       0.111111  0.111111  0.111111
'''
# ↑ 全部单元格的值相加为1

语法：

4. assign

官方文档：pandas.DataFrame.assign — pandas 1.3.0 documentation (pydata.org)

作用：Assign new columns to a DataFrame.

例：

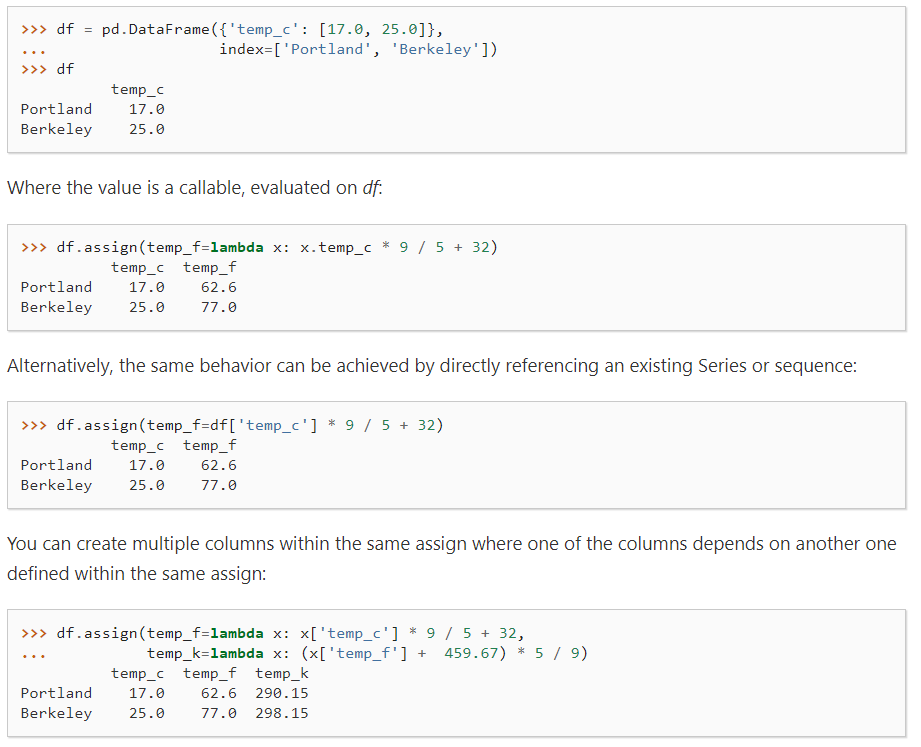
↑也可以写为：

df.assign(temp_f=lambda x:x['temp_c']*9/5+32).assign(temp_k=lambda x: (x['temp_f']+459.67)*5/9)

例：利用crosstab与assign进行woe和iv的计算：

构造数据集：

df = pd.DataFrame({"col1":["男","女","女","男","女"], "y":[0,1,1,1,0]})

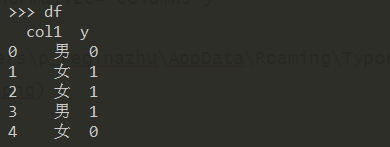
利用 crosstab 得到频率表：

pd.crosstab(df["col1"], df["y"], normalize='columns')

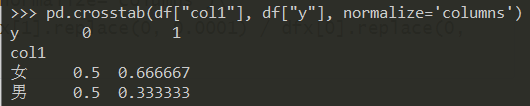
在频率表的基础上，加上woe列：

pd.crosstab(df["col1"], df["y"], normalize='columns').assign(woe=lambda dfx: np.log(dfx[1].replace(0, 0.0001) / dfx[0].replace(0, 0.0001)))

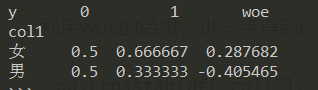
利用woe的结果，进一步得到iv：

pd.crosstab(df["col1"], df["y"], normalize='columns').assign(woe=lambda dfx: np.log(dfx[1].replace(0, 0.0001) / dfx[0].replace(0, 0.0001))).assign(iv=lambda dfx: np.sum(dfx['woe'] * (dfx[1] - dfx[0])))

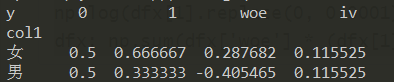
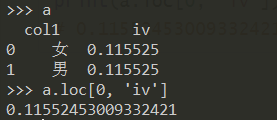
↑因为iv值是是对于一个变量而言（关于iv和woe的介绍详见我的另一篇博客 WOE编码与IV值），所以上面的两个iv值是一样的，那么如何从上述结果中提取出iv值：

df_woe_iv = pd.crosstab(df["col1"], df["y"], normalize='columns').assign(woe=lambda dfx: np.log(dfx[1].replace(0, 0.0001) / dfx[0].replace(0, 0.0001))).assign(iv=lambda dfx: np.sum(dfx['woe'] * (dfx[1] - dfx[0])))

a = df_woe_iv['iv'].reset_index()
print(a.loc[0, 'iv'])