#轻重链剖分，交互#LOJ 6669 Nauuo and Binary Tree

题目

有一棵大小为\(n\)只知道根节点为1的二叉树，

可以不超过\(3*10^4\)询问两点之间距离，

最后输出除了点1以外其余点的祖先

\(n\leq 3000\)

---

分析

\(O(n^2)\)的时间复杂度就可以了，主要是控制询问次数

首先将所有点的深度求出来，

那么询问按照点的深度递增去找该点的祖先，

有一个很重要的性质就是



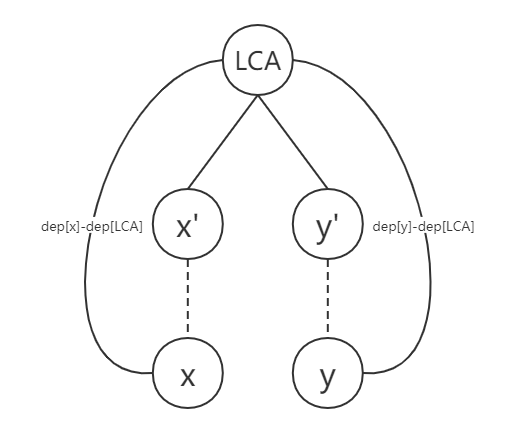
通过询问可以将\(dep[x]+dep[y]-2*dep[LCA]\)求出来，由于\(dep[x]+dep[y]\)是确定的，那么\(LCA\)也可以求出来

由于\(dep[x],dep[y]\geq dep[LCA]\)所以只要按照深度一层一层找就可以询问\(x,y\)得到它们的\(LCA\)

若当前想要找的是\(x\)的祖先，那么只要找到一个合适的\(y\)让\(dep[x]=dep[LCA]+1\)即可以让\(LCA\)变成\(x\)的祖先，

那么一定让重新找\(y\)的次数最少，考虑树上的每条路径都可以被拆分成不超过\(O(\log n)\)条重链。

从根节点开始每次找重链然后如果LCA所对应的轻儿子存在那就跳到轻儿子，则总询问次数为\(O(n+n\log n)\)实际更小

---

代码

#include <cstdio>
#include <cctype>
#include <algorithm>
#define rr register
using namespace std;
const int N=3011;
int siz[N],son[N][2],foot[N],n,rk[N],dep[N],fat[N];
inline signed iut(){
	rr int ans=0; rr char c=getchar();
	while (!isdigit(c)) c=getchar();
	while (isdigit(c)) ans=(ans<<3)+(ans<<1)+(c^48),c=getchar();
	return ans;
}
inline void print(int ans){
	if (ans>9) print(ans/10);
	putchar(ans%10+48);
}
bool cmp(int x,int y){return dep[x]<dep[y];}
inline signed Ask(int x,int y){
	putchar(63),putchar(32),print(x),putchar(32),
	print(y),putchar(10),fflush(stdout);
	return iut();
}
inline void dfs1(int x){
	siz[x]=1,foot[x]=x;
	if (son[x][0]) dfs1(son[x][0]),siz[x]+=siz[son[x][0]];
	if (son[x][1]) dfs1(son[x][1]),siz[x]+=siz[son[x][1]];
	if (siz[son[x][0]]<siz[son[x][1]]) swap(son[x][0],son[x][1]);
	if (son[x][0]) foot[x]=foot[son[x][0]];
}
inline void dfs2(int x,int y){
	rr int now=foot[x],d=Ask(now,y);
	while (dep[now]>(dep[foot[x]]+dep[y]-d)/2) now=fat[now];
	if (son[now][1]) dfs2(son[now][1],y);
	else{
	    fat[y]=now;
		if (son[now][0]) son[now][1]=y;
		    else son[now][0]=y;
	}
}
signed main(){
	n=iut();
	for (rr int i=2;i<=n;++i) dep[i]=Ask(1,i),rk[i]=i;
	sort(rk+2,rk+1+n,cmp),fat[rk[2]]=1,son[1][0]=rk[2];
	for (rr int i=3;i<=n;++i) dfs1(1),dfs2(1,rk[i]);
	putchar(33);
	for (rr int i=2;i<=n;++i) putchar(32),print(fat[i]);
	putchar(10),fflush(stdout);
	return 0;
}