神经网络之卷积篇：详解卷积步长（Strided convolutions）

详解卷积步长

卷积中的步幅是另一个构建卷积神经网络的基本操作，让向展示一个例子。

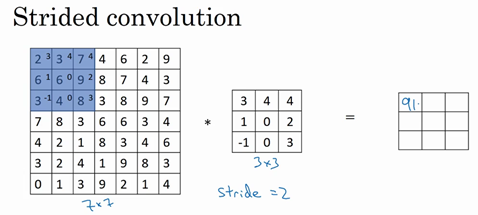
如果想用3×3的过滤器卷积这个7×7的图像，和之前不同的是，把步幅设置成了2。还和之前一样取左上方的3×3区域的元素的乘积，再加起来，最后结果为91。

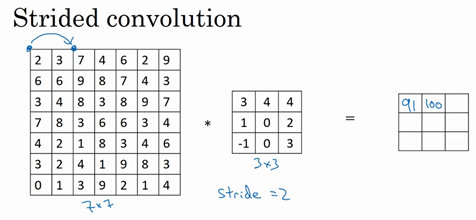
只是之前移动蓝框的步长是1，现在移动的步长是2，让过滤器跳过2个步长，注意一下左上角，这个点移动到其后两格的点，跳过了一个位置。然后还是将每个元素相乘并求和，将会得到的结果是100。

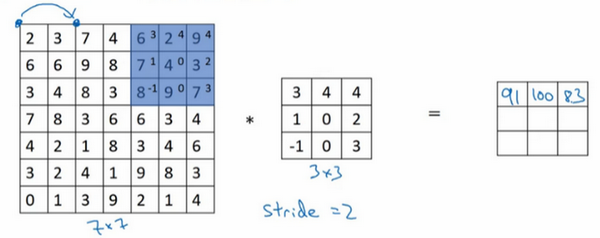
现在继续，将蓝色框移动两个步长，将会得到83的结果。当移动到下一行的时候，也是使用步长2而不是步长1，所以将蓝色框移动到这里：

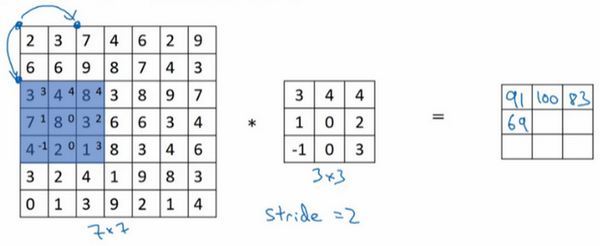
注意到跳过了一个位置，得到69的结果，现在继续移动两个步长，会得到91，127，最后一行分别是44，72，74。

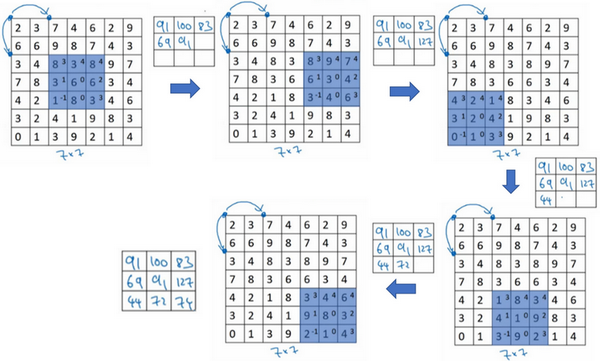
所以在这个例子中，用3×3的矩阵卷积一个7×7的矩阵，得到一个3×3的输出。输入和输出的维度是由下面的公式决定的。如果用一个\(f×f\)的过滤器卷积一个\(n×n\)的图像，padding为\(p\)，步幅为\(s\)，在这个例子中\(s=2\)，会得到一个输出，因为现在不是一次移动一个步子，而是一次移动\(s\)个步子，输出于是变为\(\frac{n+2p - f}{s} + 1 \times \frac{n+2p - f}{s} + 1\)

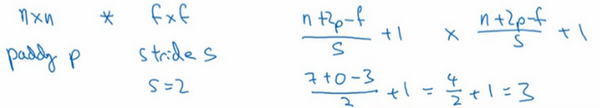
在这个例子里，\(n=7\)，\(p=0\)，\(f=3\)，\(s=2\)，\(\ \frac{7 + 0 - 3}{2} + 1 =3\)，即3×3的输出。

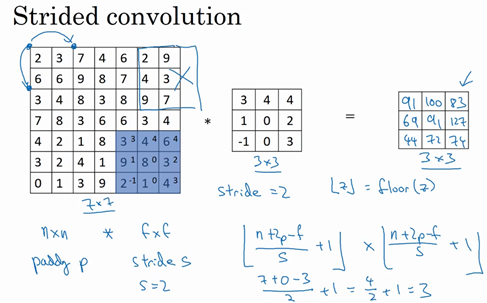
现在只剩下最后的一个细节了，如果商不是一个整数怎么办？在这种情况下，向下取整。\(⌊ ⌋\)这是向下取整的符号，这也叫做对\(z\)进行地板除(floor)，这意味着\(z\)向下取整到最近的整数。这个原则实现的方式是，只在蓝框完全包括在图像或填充完的图像内部时，才对它进行运算。如果有任意一个蓝框移动到了外面，那就不要进行相乘操作，这是一个惯例。3×3的过滤器必须完全处于图像中或者填充之后的图像区域内才输出相应结果，这就是惯例。因此正确计算输出维度的方法是向下取整，以免\(\frac{n + 2p - f}{s}\)不是整数。

总结一下维度情况，如果有一个\(n×n\)的矩阵或者\(n×n\)的图像，与一个\(f×f\)的矩阵卷积，或者说\(f×f\)的过滤器。Padding是\(p\)，步幅为\(s\)没输出尺寸就是这样：

可以选择所有的数使结果是整数是挺不错的，尽管一些时候，不必这样做，只要向下取整也就可以了。也可以自己选择一些\(n\)，\(f\)，\(p\)和\(s\)的值来验证这个输出尺寸的公式是对的。

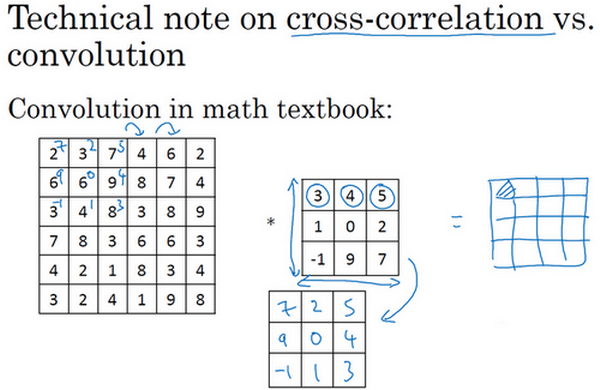
这里有一个关于互相关和卷积的技术性建议，这不会影响到构建卷积神经网络的方式，但取决于读的是数学教材还是信号处理教材，在不同的教材里符号可能不一致。如果看的是一本典型的数学教科书，那么卷积的定义是做元素乘积求和，实际上还有一个步骤是首先要做的，也就是在把这个6×6的矩阵和3×3的过滤器卷积之前，首先将3×3的过滤器沿水平和垂直轴翻转，所以\(\begin{bmatrix}3 & 4 & 5 \\ 1 & 0 & 2 \\ - 1 & 9 & 7 \\ \end{bmatrix}\)变为\(\begin{bmatrix} 7& 2 & 5 \\ 9 & 0 & 4 \\ - 1 & 1 & 3 \\\end{bmatrix}\)，这相当于将3×3的过滤器做了个镜像，在水平和垂直轴上（整理者注：此处应该是先顺时针旋转90得到\(\begin{bmatrix}-1 & 1 & 3 \\ 9 & 0 & 4 \\ 7 & 2 & 5 \\\end{bmatrix}\)，再水平翻转得到\(\begin{bmatrix} 7& 2 & 5 \\ 9 & 0 & 4 \\ - 1& 1 & 3 \\\end{bmatrix}\)）。然后再把这个翻转后的矩阵复制到这里（左边的图像矩阵），要把这个翻转矩阵的元素相乘来计算输出的4×4矩阵左上角的元素，如图所示。然后取这9个数字，把它们平移一个位置，再平移一格，以此类推。

所以在这中定义卷积运算时，跳过了这个镜像操作。从技术上讲，实际上做的，在前面使用的操作，有时被称为互相关（cross-correlation）而不是卷积（convolution）。但在深度学习文献中，按照惯例，将这（不进行翻转操作）叫做卷积操作。

总结来说，按照机器学习的惯例，通常不进行翻转操作。从技术上说，这个操作可能叫做互相关更好。但在大部分的深度学习文献中都把它叫做卷积运算，因此将在这使用这个约定。如果读了很多机器学习文献的话，会发现许多人都把它叫做卷积运算，不需要用到这些翻转。

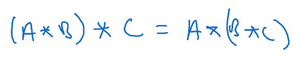
事实证明在信号处理中或某些数学分支中，在卷积的定义包含翻转，使得卷积运算符拥有这个性质，即\((A*B)*C=A*(B*C)\)，这在数学中被称为结合律。这对于一些信号处理应用来说很好，但对于深度神经网络来说它真的不重要，因此省略了这个双重镜像操作，就简化了代码，并使神经网络也能正常工作。

根据惯例，大多数人都叫它卷积，尽管数学家们更喜欢称之为互相关，但这不会影响到在编程练习中要实现的任何东西，也不会影响阅读和理解深度学习文献。