最近公共祖先 lca （施工ing）

声明

---

　　咳咳，进入重难点的图论算法之一 ： lca！（敲黑板）

　　题目： 洛谷 P3379　

---

　　一、定义

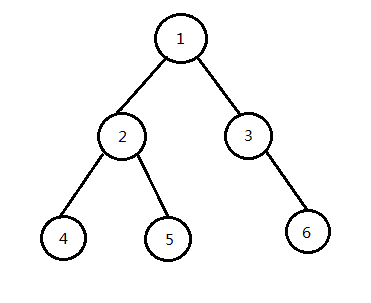
　　　　LCA 指的是最近公共祖先（Least Connon Ancestors）。具体地，给定一棵有根树，若节点 z 既是 x 的祖先，也是节点 y 的祖先，则称 z 是 x , y 的公共祖先。在 x , y 的公共祖先中，深度最大的一个节点称为 x , y 的最近公共祖先，记为 LCA（x , y）。

　　　　　我们来举个例子，如图所示：LCA（4 , 5）= 2，LCA（5 , 6）= 1，LCA（2 , 3）= 1。

　　   　

　　二、如何求 LCA

　　　　我们考虑“暴力”要怎么实现找两点的 LCA。

　　　 　　举个例子，如图： 7 , 5 的 LCA 是 2。

　　   　　   

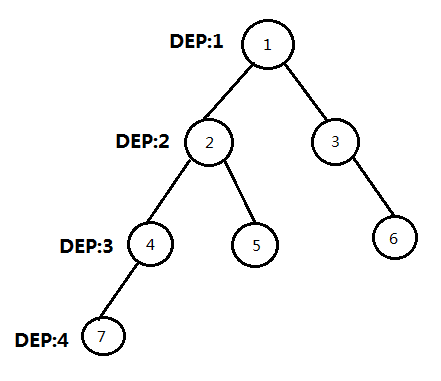
　　　　　先 DFS 一遍找出每个点的 DEP （深度）。然后先从深度大的 7 往上跳，跳到和 5 深度相同的点 4，发现还是没有到同一个点，那么 4、5 继续往上跳，直到跳到 2 位置，发现点一样了，那么 2 就是它们的 LCA 了。

---

　　三、如何优化这个方法

　　　 　　这里一共有两种方法：

　　　 　　1.离线 tarjan 求 LCA： 这里就贴一贴别人的博客吧

                　

 var
         i,j,k,n,m,s,t:longint;
         first,next,en,qfirst,qnext,qen,b,f,ans:array[..] of longint;
 procedure add(k,x,y:longint);
 begin
         next[k]:=first[x];
         first[x]:=k;
         en[k]:=y;
 end;
 procedure qadd(k,x,y:longint);
 begin
         qnext[k]:=qfirst[x];
         qfirst[x]:=k;
         qen[k]:=y;
 end;
 function find(x:longint):longint;
 begin
         if f[x]=x then exit(x) else begin f[x]:=find(f[x]); exit(f[x]) end;
 end;
 procedure tarjan(x:longint);
 var
         j,k,t:longint;
 begin
         b[x]:=;
         t:=first[x];
         while t> do
         begin
                 if b[en[t]]= then
                 begin
                         tarjan(en[t]);
                         j:=find(x);
                         k:=find(en[t]);
                         f[k]:=j;
                 end;
                 t:=next[t];
         end;
         t:=qfirst[x];
         while t> do
         begin
                 if b[qen[t]]= then
                 begin
                         ans[t]:=find(qen[t]);
                         if t mod = then ans[t+]:=ans[t]
                                 else ans[t-]:=ans[t];
                 end;
                 t:=qnext[t];
         end;
         b[x]:=;
 end;
 begin
         readln(n,m,s);
         for i:= to n- do
         begin
                 readln(j,k);
                 add(i*-,j,k);
                 add(i*,k,j);
         end;
         for i:= to m do
         begin
                 readln(j,k);
                 qadd(i*-,j,k);
                 qadd(i*,k,j);
         end;
         for i:= to n do
                 f[i]:=i;
         tarjan(s);
         for i:= to n do
                 writeln(ans[i*]);
 end.

再附上我以前的 Pascal 标程 （虽然现在不太理解）

　　　   　　2.倍增求 LCA：我们考虑这个方法慢在哪里，当然是对于每个点，一次往上跳一步，导致了效率低。那么如何优化呢？只要一次能向上跳多步，效率自然就高了。

　　　　　　树上倍增法

　　　　　　  树上倍增法是一个很重要的算法。设 f [ x , k ] 表示 x 的 2 ^k 辈祖先，即从 x 向根节点走 2 ^k 步到达的节点。特别地，若该节点不存在，则令 f [ x , k ] = 0 。f [ x , 0 ] 就是 x 的父节点。

　　　　　　  因为 x 向根节点走 2 ^k 步 ⇔ 向根走 2 ^k-1 步，再走 2 ^k-1 步（2 ^k = 2 ^k-1 + 2 ^k-1）。所以对于 k ∈ [ 1 , log n ]，有 f [ x , k ] = f [ f [ x , k-1 ] , k-1 ]。

　　　　　　  这类似于一个动态规划的过程，“阶段”就是节点的深度。因此，我们可以对树进行遍历，由此得到 f [ x , 0 ] ，再计算 f 数组的所有值。

　　　　　　  以上部分是预处理，时间复杂度为 O（n log n）。之后可以多次对不同的 x , y 计算 LCA，每次询问的时间复杂度为 O（log n）。

　　　　　　  然后基于 f 数组计算 LCA（x , y）分为以下几步：

　　　　　　　　① 设 dep [ x ] 表示 x 的深度。不妨设 dep [ x ] ≥ dep [ y ]（否则，可交换 x , y）。

　　　　　　　　② 用二进制拆分思想，把 x 向上调整到与 y 同一深度。

　　　　　　　　具体来说，就是依次尝试从 x 向上走 k = 2 ^{log n}……2 ¹，2 ⁰ 步，若到达的节点比 y 深，则令 x = f [ x , k ] 。

　　　　　　　　③ 若此时 x = y，说明已经找到了 LCA，LCA 就等于 y 。

　　　　　　　　④ 若此时 x ≠ y，那么 x , y 就继续往上跳，用二进制拆分思想，把 x , y 同时向上调整，并保持深度一致且两者不相会。

　　　　　　　　具体来说，就是依次尝试把 x , y 同时向上走 k = 2 ^{log n}……2 ¹，2 ⁰ 步，若 f [ x , k ] ≠ f [ y , k ]（即仍未相会），则令 x = f [ x , k ]，y = f [ y , k ] 。

　　　　　　　　⑤ 此时 x , y 必定只差一步就相会了，所以它们的父节点 f [ x , 0 ]（或 f [ y , 0 ]） 就是它们的 LCA !

　　　　　【代码实现】

　　　　　　　预处理：

　　　　　　　　　　void deal_first(int u,int father)
　　　　　　　　　　{
    　　　　　　　　　　dep[u]=dep[father]+;
    　　　　　　　　　　for (int i=;i<=;i++)
        　　　　　　　　　　f[u][i+]=f[f[u][i]][i];
    　　　　　　　　　　for (int e=first[u];e;e=next[e])
    　　　　　　　　　　{
        　　　　　　　　　　int v=en[e];
        　　　　　　　　　　if (v==father) continue;
        　　　　　　　　　　f[v][]=u;　　　　　　　　　　　　　　　　// v 向上跳 20=1 就是 u
        　　　　　　　　　　deal_first(v,u);
    　　　　　　　　　　}
　　　　　　　　　　}

　　　　　　　

　　　　　　　查询 x , y 的 LCA：　　　　　　

　　　　　　　　　　int lca(int x,int y)
　　　　　　　　　　{
    　　　　　　　　　　if (dep[x]<dep[y]) swap(x,y);            //让 x 的深度较大
            　　　　　//我们用“暴力”的思想：先将 x,y 跳到一个深度，然后一起往上跳
    　　　　　　　　　　for (int i=;i>=;i--)                  //一定要倒着 for
    　　　　　　　　　　{
        　　　　　　　　　　if (dep[f[x][i]]>=dep[y]) x=f[x][i]; //先跳到同一层
        　　　　　　　　　　if (x==y) return x;
    　　　　　　　　　　}
    　　　　　　　　　　for (int i=;i>=;i--)                  //此时 x,y 已跳到同一层
        　　　　　　　　　　if (f[x][i]!=f[y][i])                //如果 f[x][i]和 f[y][i] 不同才跳
        　　　　　　　　　　{
            　　　　　　　　　　x=f[x][i];
            　　　　　　　　　　y=f[y][i];
        　　　　　　　　　　}
    　　　　　　　　　　return f[x][];                          
  　　　　　　　　　　　// x,y 是深度最浅且不同的点，即 lca 的子节点
　　　　　　　　　　}

　　　　　　　然后附完整的 Pascal 标程（以前写的，步骤排列不太一样，但总体思路是差不多的）：

   　　　　　　　　　　

 var
         rmq:array[..,..] of longint;
         first,next,en,one,b:array[..] of longint;
         deep,a:array[..] of longint;
         i,j,k,m,n,s,t,l,r:longint;
 procedure add(k,x,y:longint);
 begin
         next[k]:=first[x];
         first[x]:=k;
         en[k]:=y;
 end;
 procedure getrmq;
 begin
         for i:= to k do
                 rmq[i,]:=i;
         for j:= to  do
                 for i:= to k do
                         if i+(<<j)-<=k then
                                 if deep[rmq[i,j-]]<deep[rmq[i+(<<(j-)),j-]]
                                         then rmq[i,j]:=rmq[i,j-]
                                                 else rmq[i,j]:=rmq[i+(<<(j-)),j-];
 end;
 function que:longint;
 begin
         t:=trunc(ln(r-l+)/ln());
         if deep[rmq[l,t]]<deep[rmq[r-(<<t)+,t]] then exit(a[rmq[l,t]])
                 else exit(a[rmq[r-(<<t)+,t]]);
 end;
 procedure dfs(x,y:longint);
 var
         t:longint;
 begin
         inc(k);
         deep[k]:=y;
         b[x]:=;
         a[k]:=x;
         t:=first[x];
         while t> do
         begin
                 if b[en[t]]= then
                 begin
                         dfs(en[t],y+);
                         inc(k);
                         a[k]:=x;
                         deep[k]:=y;
                 end;
                 t:=next[t];
         end;
         b[x]:=;
 end;
 begin
         readln(n,m,s);
         for i:= to n- do
         begin
                 readln(j,k);
                 add(i*-,j,k);
                 add(i*,k,j);
         end;
         k:=;
         dfs(s,);
         for i:= to k do
                 if b[a[i]]= then
                 begin
                         one[a[i]]:=i;
                         b[a[i]]:=;
                 end;
         getrmq;
         for i:= to m do
         begin
                 readln(j,k);
                 l:=one[j];
                 r:=one[k];
                 if l>r then
                 begin
                         j:=l;
                         l:=r;
                         r:=j;
                 end;
                 writeln(que);
         end;
 end.

自己现在不理解的 Pascal 标程

---

　　四、习题

　　　　　　1 . 洛谷 P3258：松鼠的新家（LCA+树上差分，当然也可以用树链剖分做）　　　　

　　　　　　　　　　

 #include<cstdio>
 #include<algorithm>
 #include<cmath>

 using namespace std;

 int n,x,y,tot,s,t;
 int first[],next[],en[];
 int ans[],dep[],f[][],a[];

 void deal_first(int u,int father)
 {
     dep[u]=dep[father]+;
     for (int i=;i<=;i++)
         f[u][i+]=f[f[u][i]][i];
     for (int e=first[u];e;e=next[e])
     {
         int v=en[e];
         if (v==father) continue;
         f[v][]=u;
         deal_first(v,u);
     }
 }

 int lca(int x,int y)
 {
     if (dep[x]<dep[y]) swap(x,y);
     for (int i=;i>=;i--)
     {
         if (dep[f[x][i]]>=dep[y]) x=f[x][i];
         if (x==y) return x;
     }
     for (int i=;i>=;i--)
         if (f[x][i]!=f[y][i])
         {
             x=f[x][i];
             y=f[y][i];
         }
     return f[x][];
 }

 void add(int x,int y)
 {
     next[++tot]=first[x];
     first[x]=tot;
     en[tot]=y;
 }

 void updata(int u,int father)
 {
     for (int e=first[u];e;e=next[e])
     {
         int v=en[e];
         if (v==father) continue;
         updata(v,u);
         ans[u]+=ans[v];
     }
 }

 int main()
 {
     scanf("%d\n",&n);
     for (int i=;i<=n;i++)
         scanf("%d",&a[i]);
     for (int i=;i<n;i++)
     {
         scanf("%d%d",&x,&y);
         add(x,y);
         add(y,x);
     }
     deal_first(,);
     for (int i=;i<n;i++)
     {
         int LCA=lca(a[i],a[i+]);
         ans[a[i]]++;
         ans[a[i+]]++;
         ans[LCA]--;
         ans[f[LCA][]]--;
     }
     updata(,);

     //每条路的终点会同时作为下条路的起点重复+1
     //最后的终点不会重复，但题目说不要+1
     //于是每条路的终点我们都加多了一次
     //所以现在将每条路的终点都-1
     for (int i=;i<=n;i++)
         ans[a[i]]--;

     for (int i=;i<=n;i++)
         printf("%d\n",ans[i]);
     return ;
 }

C++ 标程（差分时记得去重）

　　　　

---

以上内容部分借鉴于：《信息学奥赛一本通 · 提高篇（第一版）》