K-means + PCA + T-SNE 实现高维数据的聚类与可视化
使用matlab完成高维数据的聚类与可视化
[idx,Centers]=kmeans(qy,)
[COEFF,SCORE,latent] = pca(qy);
SCORE = SCORE(:,:);
mappedX = tsne(SCORE,'Algorithm','exact','NumDimensions',);
c=zeros(,);
for i = :
c(i,idx(i)) = ;
end
scatter3(mappedX(:,),mappedX(:,),mappedX(:,),,c,'fill') % 数据qy为211个,48维。
% K-means: [idx,Centers]=kmeans(data,k)
% 将数据分为k类,idx为每个数据的类别标号,centers为k个中心的坐标, % PCA: [COEFF SCORE latent]=princomp(X)
% 现在已经改名为pca而非princomp
% 参数说明:
% )COEFF 是主成分分量,即样本协方差矩阵的特征向量;
% )SCORE主成分,是样本X在低维空间的表示形式,即样本X在主成份分量COEFF上的投影 ,若需要降k维,则只需要取前k列主成分分量即可
% )latent:一个包含样本协方差矩阵特征值的向量; % T-SNE: mappedX = tsne(X, labels, no_dims, init_dims, perplexity)
% tsne 是无监督降维技术,labels 选项可选;
% X∈RN×D,N 个样本,每个样本由 D 维数据构成;
% no_dims 的默认值为 ;(压缩后的维度)
% tsne 函数实现,X∈RN×D⇒RN×no_dimes(mappedX)
% init_dims:注意,在运行 tsne 函数之前,需要使用 PCA 对数据预处理,将原始样本集的维度降低至 init_dims 维度(默认为 )。
% perplexity:高斯分布的perplexity,默认为 ;
最终效果:
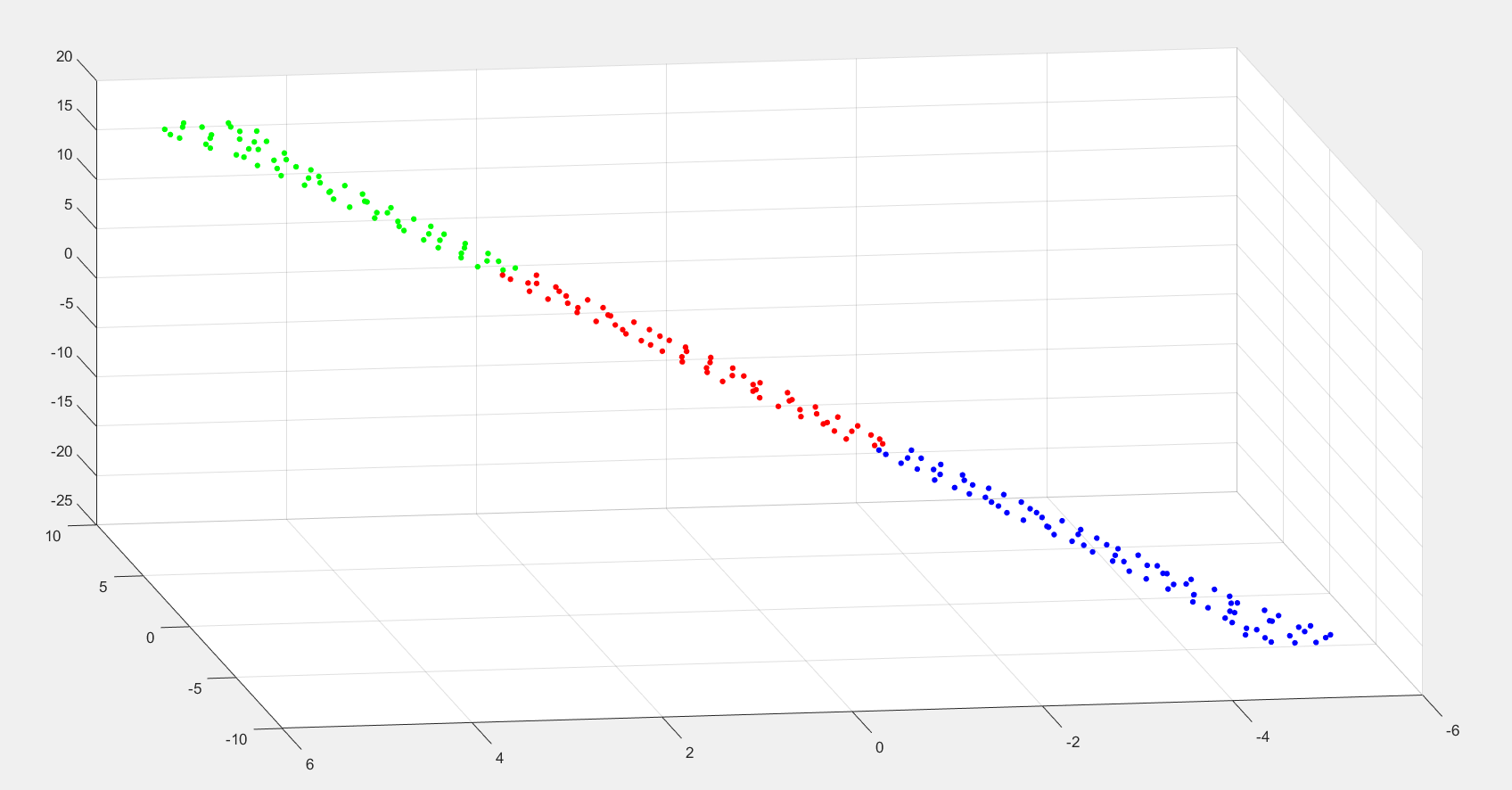
K-means + PCA + T-SNE 实现高维数据的聚类与可视化的更多相关文章
- 机器学习:PCA(高维数据映射为低维数据 封装&调用)
一.基础理解 1) PCA 降维的基本原理 寻找另外一个坐标系,新坐标系中的坐标轴以此表示原来样本的重要程度,也就是主成分:取出前 k 个主成分,将数据映射到这 k 个坐标轴上,获得一个低维的数据集. ...
- 基于Hash算法的高维数据的最近邻检索
一.摘要 最紧邻检索:一种树基于树结构,一种是基于hash a.随机投影算法,需要产生很多哈希表,才能提高性能. b.基于学习的哈希算法在哈希编码较短时候性能不错,但是增加编码长度并不能显著提高性能. ...
- PCA算法详解——本质上就是投影后使得数据尽可能分散(方差最大),PCA可以被定义为数据在低维线性空间上的正交投影,这个线性空间被称为主⼦空间(principal subspace),使得投影数据的⽅差被最⼤化(Hotelling, 1933),即最大方差理论。
PCA PCA(Principal Component Analysis,主成分分析)是一种常用的数据分析方法.PCA通过线性变换将原始数据变换为一组各维度线性无关的表示,可用于提取数据的主要特征分量 ...
- 【笔记】求数据前n个主成分以及对高维数据映射为低维数据
求数据前n个主成分并进行高维数据映射为低维数据的操作 求数据前n个主成分 先前的将多个样本映射到一个轴上以求使其降维的操作,其中的样本点本身是二维的样本点,将其映射到新的轴上以后,还不是一维的数据,对 ...
- 高维数据的高速近期邻算法FLANN
版权声明:本文为博主原创文章,未经博主同意不得转载. https://blog.csdn.net/jinxueliu31/article/details/37768995 高维数据的高速近期邻算法FL ...
- 利用 t-SNE 高维数据的可视化
利用 t-SNE 高维数据的可视化 具体软件和教程见: http://lvdmaaten.github.io/tsne/ 简要介绍下用法: % Load data load ’mnist_trai ...
- 高维数据降维 国家自然科学基金项目 2009-2013 NSFC Dimensionality Reduction
2013 基于数据降维和压缩感知的图像哈希理论与方法 唐振军 广西师范大学 多元时间序列数据挖掘中的特征表示和相似性度量方法研究 李海林 华侨大学 基于标签和多特征融合的图像语义空间学习技 ...
- 高维数据Lasso思路
海量数据的特征工程中, 如果数据特征维度达到几千乃至上万 常规的lasso很容易失效 这里介绍几种泛义lasso,是在实际数据处理中常用的 迭代与分块思路/分组的使用(有兴趣的同学可自行实践一下) 1 ...
- EM 算法-对鸢尾花数据进行聚类
公号:码农充电站pro 主页:https://codeshellme.github.io 之前介绍过K 均值算法,它是一种聚类算法.今天介绍EM 算法,它也是聚类算法,但比K 均值算法更加灵活强大. ...
随机推荐
- Struts2框架学习笔记--strtus2初识
struts2概述: 1.struts2框架应用于javaEE三层结构中的Web层框架 2.struts2框架是在struts1和webwork基础之上发展的全新框架(脱胎换骨 ,用法完全不一样)ps ...
- DG不同步,MRP0进程打不开
问题描述:主库备库之前正常连接,但是昨天磁盘空间满了之后,由于不知什么原因将备库重做日志删了,今天早上发现DG不同步的报警. 当时思路如下:1.通过select thread#,low_sequenc ...
- oracle 子查询的几个种类
1.where型子查询: select cat_id,good_id,good_name from goods where good_id in (selct max(good_id) from go ...
- Web—13-判断网站请求来自手机还是pc浏览器
判断网站请求来自手机还是pc浏览器 #判断网站来自mobile还是pc def checkMobile(request): """ demo : @app.route(' ...
- Instruments Time profiler 调优APP 之图片解码
以前闲时用instruments的Time profiler调试过APP,发现用tableView: cellForRowAtIndexPath: 中cell的图片设置耗时较多,之前改了一下,如下 d ...
- C++笔记020:const 和 #define 的对比
原创笔记,转载请注明出处! 点击[关注],关注也是一种美德~ 第一,const与#define的相同点 C++中的const常量类似于宏定义 const int c = 5 ≍ #defi ...
- MySQL更新丢失
MySQL多主结构(比如: MGR Multi Master模式),如果多主都可以写的话,很有可能出现更新丢失的情况. 定义: T1时间,T2时间,T3时间 定义: 事务A, 事务B Node1节 ...
- 解决mysql远程登录
MySQL不允许远程登录,所以远程登录失败了,解决方法如下: 在装有MySQL的机器上登录MySQL mysql -u root -p密码 执行use mysql; 执行update user set ...
- ES6学习之-let 和const命令
let 和const命令 let命令 用来声明变量,类似于var .let声明的变量 只在let命令所在的代码块内有效. 在for循环里也是如此 每次循环其实都是一个代码块 function fn() ...
- [FreeRTOS入门] 1.CubeMX中FreeRTOS配置参数及理解
1.有关优先级 1.1 Configuration --> FreeRTOS MAX_PRIORITIES 设置任务优先级的数量:配置应用程序有效的优先级数目.任何数量的任务都可以共享一个优先级 ...
